Рассмотрена математическая модель движения подводного аппарата с шестью управляющими воздействиями, решена терминальная задача управления движением аппарата и построено программное управление с использованием метода обратных задач динамики.

Рассмотрена нелинейная управляемая механическая система многих тел, состоящая из несущего диска, вращающегося вокруг своей оси, закрепленной в пространстве, и несомого диска, присоединенного к нему при помощи невесомых упругих элементов. С помощью метода последовательных приближений на достаточно большом интервале времени решена задача о раскручивании системы посредством момента сил, приложенного к несущему диску, с одновременным оптимальным гашением колебаний центра масс несомого диска.

Для колебательной системы с механизмом возбуждения как в классическом осцилляторе Релея, но с нелинейной (кубической) возвращающей силой, для широкого диапазона значений коэффициента обратной связи построены предельные циклы и вычислены амплитуды и периоды автоколебаний. Проведен анализ особенностей предельного цикла, вызванных увеличением коэффициента самовозбуждения. Полученные результаты могут быть сопоставлены с автоколебаниями классического осциллятора Релея с линейной возвращающей силой.

Исследуется математическая модель мозгового кровообращения. Задача моделирования механизма авторегулирования мозгового кровотока рассматривается как задача автоматического управления, заключающаяся в отслеживании заданного выходного сигнала. Для синтеза стабилизирующих законов управления модели кровотока используется метод стабилизации по первому приближению. Для оценки состояния системы построен линейный наблюдатель. Записана линейная обратная связь по оценке состояния системы наблюдателем

Рассматривается движение инерционного объекта при управляемом скоростном манёвре в вертикальной плоскости. Решается задача максимизации горизонтальной проекции скорости в заданный конечный момент времени для оптимального и двух предложенных субоптимальных управлений. Исследуется условие разрешимости, связанное с минимально возможным временем движения, которое требуется для выполнения граничных условий. Проводится сравнительный анализ траектории при разных управлениях и начальных условиях.

Разработан прототип робототехнического комплекса, предназначенного для установки робота вертикального перемещения на обслуживаемую поверхность в автоматическом режиме. Реализованы алгоритмы адаптивного управления манипулятором и колесной платформой комплекса, которые были предложены ранее. Алгоритмы управления учитывают неопределенность геометрических и инерционных параметров робототехнического комплекса, а также позволяют компенсировать неидеальность его приводов.

Ставится задача оптимального управления теплопередачей в стержнях, соединенных последовательно термоэлектрическими преобразователями. Для фиксированного времени ищется функция управляющего теплового потока, которая приводит один из стержней в состояние с заданной температурой. Для расчетов с помощью МКЭ используется интегральное представление законов состояния. Предлагается регуляризация задачи управления, которая обеспечивается добавлением к целевому функционалу интеграла состояния.

Рассматривается задача моделирования распространения внутренних гравитационных волн от движущегося в толще идеальной стратифицированной жидкости массового источника. Жидкость может иметь произвольный профиль стратификации по глубине. Показано соответствие результатов расчетов  разработанной компьютерной программы асимптотикам дальнего поля для случаев, когда жидкость равномерно стратифицирована, а источник движется равномерно и прямолинейно горизонтально или под углом к горизонту.

В данной работе с привлечением методов обучения с подкреплением решаются две задачи оптимального управления: максимизации средней скорости агента (капсульного робота) и наискорейшего приведения агента из точки А в точку Б с остановкой там. Управление должно быть кусочно-постоянной функцией по аналогии с ШИМ сигналом, а также иметь воспроизводимую на реальном роботе частоту. Моделирование производилось в созданных авторами виртуальных окружениях, соответствующих интерфейсу OpenAI GYM.

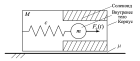
Рассмотрены задачи об оптимизации закона управления движением капсульного робота с возвратной пружиной и электромагнитным приводом с помощью метода Nonlinear Model Predictive Control (NMPC). В рамках первой задачи найден закон управления, оптимизирующий среднюю скорость центра масс капсульного робота, во второй задаче найден закон управления, реализующий перемещение капсульного робота на заданное расстояние за минимальное время.

Рассмотрено применение гетерогенной системы в задачах мониторинга местности. Разработан математический аппарат определения скорости наземной зарядной станции для одновременного прибытия в точку посадки БПЛА. Смоделировано движение робототехнических систем на разных многоугольниках.

Исследуется влияние наклонения орбиты космической станции при движении по окололунной орбите на процесс развёртывания радиально направленной космической тросовой системы, состоящей из космической станции и прикреплённых к ней с помощью тросов двух малых космических аппаратов, рассматриваемых как материальные точки. Выпуск тросов происходит по закону управления, обеспечивающему развёртывание тросов на заданную длину при малых отклонениях от положения местной вертикали.