Работа посвящена исследованию субградиентных методов с различными вариациями шага Б. Т. Поляка на классах задач минимизации слабо выпуклых и относительно слабо выпуклых функций, обладающих соответствyющим аналогом острого минимума.

Данная работа фокусируется на решения негладких выпуклых стохастических задач оптимизации. Одним из способов решения таких задач является применение безградиентных алгоритмов оптимизации. В данной работе мы обобщаем схему сглаживания с l1 рандомизацией на негладкую настройку. На примере архитектуре федеративного обучения (в гомогенном случае) сравниваем безградиентные алгоритмы, созданные с помощью двух техник сглаживания: l1 и l2 рандомизациями.

Рассматривается проблема ограниченного марковского процесса принятия решений. Агент стремится максимизировать ожидаемую накопленную дисконтированную награду с учетом многочисленных ограничений на затраты. Предложен новый двойственный подход с интеграцией двух компонентов: энтропийно-регуляризованного оптимизатора политики и двойного оптимизатора Vaidya. 

Обычные алгоритмы распределенной оптимизации уязвимы к так называемым Византийским атакам - посылкам данных, отличающихся от привычного поведения. В последнее время все больше внимания уделяют разработке робастных методов, например, используя редукцию дисперсии и робастную агрегацию. В этой работе мы предложим новый метод на основе оценщика SVRG - BR-LSVRG. Мы будем исследовать сходимость метода в гладком и сильно выпуклом случае и сравнивать его эффективность с уже существующими методами.

В данной работе предложен способ решения обратной задачи на гиперболическом уравнении теплопроводности с малым параметром, предложен способ получения оптимального размера сетки с помощью обучения на больших размерах сетки и малом числе итераций градиентного метода. Этот подход можно применять в задачах с похожей структурой, например в исследовании социальных процессов или в различных биологических задачах. 

В работе рассмотрен процесс проектирования системы управления кустом добывающих скважин месторождений минеральных вод с определением оптимального числа скважин, включая построение математической и дискретной модели, их верификацию и синтез регуляторов. Описана методика решения задачи оптимизации с использованием спектров Гершгорина, которая позволяет определить оптимальное число взаимодействующих скважин, и обеспечивает максимизацию дохода с учетом параметров рассматриваемого месторождения.

Работа посвящена исследованию нескольких подходов к построению адаптивных методов градиентного типа для относительно гладких и относительно липшицевых задач выпуклой оптимизации.

В данной работе представлены нижние оценки сложности для гладких сильно-выпуклых сильно-вогнутых седловых задач с композитами. Также предложены оптимальные алгоритмы (которые достигают нижних оценок) для данного класса задач. Предложенный подход позволяет разделить сложность по композитам и седловой части.

Оптимизация случайных процессов перезапуском является предметом активных исследований в статистической физике и находит практическое применение в программировании. Один из ключевых вопросов: как следует перезапускать процесс, детальная статистика которого неизвестна, чтобы быть уверенным, что алгоритм не ухудшит производительность? Здесь мы строим конструктивистские критерии эффективности перезапуска для задач оптимизации среднего времени завершения и оптимизации вероятностей расщепления. 

Биологические наблюдения показали, что кооперация склонна проявляться при ограниченности ресурсов и жесткой межгрупповой конкуренции. Несмотря на распространённость эмпирических наблюдений, до сих пор не была введена теоретико-игровая модель, в которой можно было бы подтвердить этот и другие наблюдаемые эффекты. В рамках данной работы предлагается модель, которая устраняет проблемы ранее существующих и пронаблюдать некоторые эффекты в процессе моделирования равновесных по Нэшу состояний.

В данной работе показан процесс проведения закупки между поставщиками, а также конкуренции между ними. Большая часть закупок в образовательной сфере осуществляется по принципу Байесовой игры, в которой поставщики не обладают информацией о функциях полезности друг друга, причем закупка будет являться закрытым аукционом первой цены. Рассмотрен общий случай для поведения n поставщиков, максимизирующих прибыль и случай участия в закупке поставщиков, максимизирующих прибыль или выручку.

В докладе рассматривается линейная система управления, подверженная воздействию внешних возмущений и системных неопределенностей. Предложен регулярный подход к синтезу обратной связи, минимизирующей величину максимального отклонения ее траектории. Подход предполагает сведение исходной задачи к параметрической задаче полуопределенного программирования, легко решающейся численно. Он в равном объеме охватывает случаи как непрерывного, так и дискретного времени.

(Заявка на дистанционное участие)

В работе рассматривается фактическое время работы алгоритмов 1) Метода последовательной итерации 2) Метода Поляка-Трембы 3) Метода Франка-Вульфа 4) Метода Монте-Карло поиска вектора PageRank для различных порядков точностей вектора PageRank. Таким образом, полученный метод позволяет оценить время вычисления вектора PageRank для различных графов с учётом числа вершин, ребёр, параметра кластеризации и прочих. 

В данной работе рассмотрено решение задачи планирования тяговых ресурсов на железной дороги с использованием потокового алгоритма

Рассмотрено получение функций чувствительности одноканального дискретного ПИ-регулятора. Данные функции чувствительности позволяют через моделирование получить беспоисковым способом производные первого  порядка интегрального квадратичного критерия оптимизации по настраиваемым параметрам этого регулятора. Это позволяет реализовать градиентную процедуру для решения задачи параметрическом синтезе дискретного регулятора температуры электропечи.

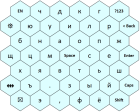
В работе описан быстрый и эффективный метод стохастической оптимизации для получения оптимальной раскладки  виртуальной клавиатуры с квадратными или шестиугольными клавишами.

Работа посвящена анализу сходимости класса градиентно-согласованных методов для функций, удовлетворяющих условию Поляка-Лоясиевича. Показано, что сходимость является линейной, и дана оценка параметра сходимости. Теоретическая оценка скорости сходимости сопоставлена с данными численного эксперимента.

Нетерминальной сложностью контекстно-свободного языка называется минимальное возможное количество нетерминалов в грамматике, порождающей данный язык. В общем случае, вычисление нетерминальной сложности языка является алгоритмически неразрешимой задачей. В данной работе рассматривается нетерминальная сложность некоторых семейств регулярных языков.

В данной работе предложен алгоритм светофорного регулирования транспортной сети, основанный на методах предиктивного управления и безградиентной оптимизации. Было проведено тестирование предложенного подхода в программной среде SUMO и сравнение различных алгоритмов оптимизации.

Приведен пример полугруппы, заданной порождающими и соотношениями, функция Дэна которой асимптотически равна $$n \mathrm{log} n$$, то есть лежит строго между линейной и квадратичной.

Работа посвящена решению некоторых обратных задач математической физики, которые сводятся к задачам выпуклой оптимизации в гильбертовом пространстве. Предлагается метод решения - покомпонентный спуск в базисе из собственных функций связанного с задачей оператора. Экспериментально определяется, что новый подход превосходит подходы, основанные на использовании градиентных методов оптимизации: он позволяет достичь лучшего качества решения при значительно меньшем расходе вычислительных ресурсов.

В данной работе исследовался вариант метода Франк-Вульфа для задач выпуклой оптимизации с адаптивным выбором параметра шага, соответствующего информации о гладкости целевой функции (константа Липшица градиента). Получены теоретические оценки качества решения, обеспечиваемого методом, через адаптивно подобранные параметры $L_k$. Проведены численные эксперименты, показывающие эффективность данного алгоритма для некоторых негладких задач.

В данной работе исследуются различные вариации автоматов со словарём и определяются классы языков, распознаваемых полученными моделями вычислений.