В работе строится асимптотическое решение уравнения Гелмгольца с гамильтонианом H = h^2Δ+(bx)^2+a^2 и локализованной правой частью, а также пишется точное решение в виде интеграла для правой части в виде δ-функции

Исследуются коротковолновые асимптотические решения задачи Коши для волнового уравнения с быстро меняющейся скоростью. А именно, предполагается, что скорость имеет сглаженный скачок вблизи гладкой гиперповерхности. Мы описываем распространение коротковолновых пакетов, а также локализованных пучков; для этих случаев мы находим правила перестройки геометрических объектов, которые определяют решение. В результате получаем полный асимптотический ряд для решения задачи Коши

• Рассматривается задача о построении асимптотики собственных значений и собственных функций для одномерного оператора Шрёдингера с потенциалом, имеющим локализованное возмущение.

Рассматривается задача о построении асимптотических собственных функций оператора Лапласа в трехмерной области, ограниченной двумерным тором, на котором задаётся условие Дирихле. 

Рассмотрена квазиклассическая асимптотика решения задачи Коши для уравнения Шредингера с дельта-потенциалом, локализованным на поверхности коразмерности 1.

В работе приводится метод, позволяющий получить равномерные асимптотики в виде функций Эйри для функций параболического цилиндра, а также для собственных функций оператора Шредингера с потенциалом в виде негладкой двойной ямы. Обсуждается также условие квантования на точки спектра в окрестности переходного уровня ямы.  Метод основан на модификации теории канонического оператора и исследовании соответствующих лагранжевых многообразий.  

Доклад посвящён построению глобальных асимптотик полиномов Лагерра, как решений разностного уравнения при больших значениях индекса. Подход к построению асимптотики основан на квазиклассическом приближении и изучении особенностей соответствующего лагранжева многообразия.

Рассматривается движение жидкости в двумерной вертикальной трубе с помощью одномерной системы на давление, энтропию и продольную скорость (осредненные в поперечном направлении). Эта система моделирует эффект запирания потока: при увеличении тепловыделения до определенного порога скорость обращается в нуль. В работе исследуется влияние тепловыделения на изменение параметров потока, а также влияние силы тяжести и параметров уравнения состояния на критическое значение тепловыделения.

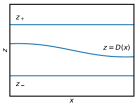
При изучении звуковых волн в океане, порожденных точечным источником, возникает уравнение Гельмгольца с соответствующими условиями на границе раздела двух сред (жидкость-дно) с локализованной в окрестности точки правой частью. В работе строится его асимптотическое по малому параметру (отношение вертикального и горизонтальных масштабов задачи) решение.

Поверхностные волны на воде над неровным дном описываются уравнением с псевдодифференциальным оператором. Рассмотрим одномерный случай и поставим задачу Коши с локализованным начальным условием и краевым условием непротекания на жесткой вертикальной стенке. В работе исследуется отражение волны от стенки и влияние дисперсии. Асимптотики задачи строятся в виде канонического оператора с использованием метода отражений. В окрестности головного фронта асимптотика выражается через функцию Эйри.

В работе строится точное решение волнового уравнения на конусе. Лапласиан, входящий в волновой оператор, есть произвольное самосопряженное расширение оператора Лапласа-Бельтрами, заданного на финитных функциях, носитель которых отделен от вершины. Расширение задается граничным условием в окрестности вершины. Для построения решения находится система собственных функций лапласиана и вычисляются их нормировочные коэффициенты.