Все любят смотреть мультфильмы – и взрослые, и дети. Но всё, что мы видим – это готовая картинка, интересные герои и сюжет. Всё самое сказочное и интересное остаётся за кадром. Как интересно самому придумать сценарий, нарисовать персонажей и создать мультфильм!

Цель работы – создание мультфильма в домашних условиях.

Задачи:

1. изучение литературы;
2. изучение различных технологий создания фото-мультфильмов;
3. выбор оборудования;
4. изучение возможностей компьютерных программ для создания мультипликационных фильмов;
5. разработка и создание мультфильмов при помощи различных технологий.

1. Название научно-исследовательской работы: «Робот Lego Mindstorms – модель автомобильной оптики»
2. ФИО автора: Водальчук Михаил Николаевич
3. Образовательное учреждение: МБОУШР «Гимназия»
4. Руководитель: Водальчук Светлана Алексеевна, учитель ИиИКТ МБОУ ШР «Гимназия»
5. Краткая постановка целей и задач исследования.

Цель работы – разработка модели автомобильной оптики при помощи конструктора Lego Mindstorms. Гипотеза – возможность создания модели автомобильной оптики при помощи конструктора Lego Mindstorms.

Задачи:

1. Изучение литературы;
2. Изучение возможностей конструктора Lego Mindstorms;
3. Изучение оптики автомобиля;
4. Конструирование робота Lego Mindstorms – модели автомобильной оптики;
5. Программирование робота Lego Mindstorms.
6. Основной текст тезисов.

Наша идея и гипотеза исследования заключается в том, чтобы создать модель автомобильной оптики при помощи конструктора Lego Mindstorms. Таким образом, необходимо собрать автомобиль на колесах, имеющий 10 фар: габаритные фары – 4 шт.; фары поворота – 4 шт.; стоп-сигналы – 2 шт. В качестве фар будут использоваться лампы, входящие в комплект конструктора. Блок управления содержит 7 портов для подключения моторов и датчиков. Этого количества недостаточно для подключения фар, поэтому решено использовать два блока управления. Два блока управления невозможно запустить одновременно нажатием какой-либо одной кнопки. Поэтому запуск автомобиля производится нажатием двух кнопок на блоках управления, что крайне неудобно.

Два блока управления значительно утяжеляют конструкцию. Поэтому необходимо собрать устойчивый автомобиль на 4 колесах, но при этом автомобиль должен быть маневренным и поворачивать.

В процессе сбора модели пришли к проблеме поворота автомобиля на 4-х колесах. Поворот автомобиля осуществляется за счет увеличения мощности колес одной стороны (например, правой) и уменьшения мощности колес другой стороны (например, левой). Это единственная возможность Lego-роботов совершать повороты. Для машины на 4-х колесах при повороте колеса одной из сторон «идут юзом», то есть препятствуют совершению поворота. Таким образом, от идеи создания автомашины на 4-х колесах пришлось отказаться. Для маневренности конструкции автомобиль должен иметь 3 колеса.

Так же возникли проблемы, связанные с особенностями конструктора Lego Mindstorms. Блок управления имеет порты двух видов: 1, 2, 3, 4 и А, В, С. К портам 1, 2, 3, 4 можно подключать датчики касания, звука, освещенности, расстояния, цвета.  К портам А, В, С можно подключать моторы, лампы. Таким образом, необходимые для подключения ламп порты А, В, С (6 портов), будут заняты моторами, которых должно быть не менее двух. Моторы приводят в движение колеса автомобиля. Следовательно, нет возможности подключить 10 ламп к четырем свободным портам А, В, С. Эту проблему можно решить, сократив количество фар и заменив лампы на датчики освещенности. Основное назначение датчиков освещенности заключается в том, что они «сканируют» уровень освещенности. Мы будем использовать эти датчики не по назначению. Нам необходим свет, который могут излучать эти датчики.

Итак, наш автомобиль, иллюстрирующий модель автомобильной оптики, будет содержать 4 осветительных прибора – 2 фары в передней части, 2 фары в задней части автомобиля.

• Передние фары – будут загораться белым светом при движении автомобиля вперед. В качестве этих фар будем использовать лампы конструктора.
• Фары заднего хода – будут загораться красным светом при движении автомобиля назад. В качестве этих фар будем использовать два датчика освещенности.
• Фары поворота.

6. Актуальность исследования.

Конструкторы Lego Mindstorms недавно стали использоваться в школах России. Очень мало учебной литературы на русском языке и информации в сети Интернет, описывающей готовые модели роботов (технических устройств). Поэтому данная работа является новой, неизученной и актуальной.

7. Значимость и новизна исследования.

Любой ребенок, особенно мальчишка, любит играть детскими машинками. Но, куда более интереснее, создать автомобиль своими руками. Сегодня, конструкторы  Lego дают эту возможность. Конструктор Lego Mindstorms имеет возможность не только конструирования моделей (роботов), но и их программирования.

8. Литература.

• Копосов Д.Г. Первый шаг в робототехнику. – М: Бином. Лаборатория знаний, 2014.
• Филиппов С.А. Робототехника для детей и родителей.– СПб.: Наука, 2013.
• Справка и техподдержка Lego Mindstorms Education NXT.
• wikipedia.org – Википедия. Свободная энциклопедия.

Новые возможности MS Excel

Шулепов Егор Анатольевич

Иркутская обл., г.Шелехов

МБОУШР «Гимназия», 8 класс

Водальчук Светлана Алексеевна

Учитель информатики и математики

МБОУШР «Гимназия»

Назначение табличного процессора Microsoft Excel известно многим, и даже «непродвинутым» пользователям. Электронные таблицы MS Excel предназначены, в первую очередь, для автоматизированного подсчета по формулам. Однако, MS Excel можно использовать для создания динамичных объектов. В процессе работы над темой исследования самостоятельно созданы примеры  динамических эффектов на основе форматирования символов, изменения графических объектов и на основе встроенных функций электронных таблиц. К каждому примеру разработан подробный алгоритм создания, приведена программа на VBA (Visual Basic for Application).

Распределение кроликов по клеткам и не только... Задачи раскрашивания графов

Павлов Л.Е., Шамаев С.А.

Россия, Липецкая область, г. Липецк

гимназия № 12, гимназия №64 им. В.А.Котельникова, ЦДО «Стратегия», 4 класс

Научный руководитель: к.т.н., доц.кафедры прикладной математики Липецкого государственного технического университета Шуйкова И.А.

Аннотация работы

Целью работы является изучение жадного алгоритма раскраски вершин графа и практических приложений этой задачи.

Методы, используемые в работе: в работе используются методы оперирования с простейшими геометрическими фигурами, методы комбинаторики для анализа исследуемых объектов, начальные знания по теории графов.

Задачи работы. В ходе исследования были поставлены следующие задачи:

1. изучение литературы по теме исследования: изучение истории математической проблемы «четырех красок»; изучение художественной литературы, отражающей исследуемую проблему; знакомство с жадным алгоритмом раскраски вершин графа.
2. Проведение серии практических экспериментов по исследованию жадного алгоритма – раскрашивание вершин графа при различном обходе вершин графа.
3. Формализация двух практических задач в виде раскраски вершин графа.
4. Подготовка математического буклета «Раскраска вершин графа» на основе материалов проделанной работы.
5. Создание научно-популярного фильма «Остров пяти красок»

Основной текст тезисов

     Исследовательская работа является продолжением практического исследования, начатого нами в прошлом году. Первый год работы был посвящен проблеме четырех красок, которая известна уже более 100 лет. Мы, как и математики, начали с проверки утверждения четырех красок для различных карт. Сначала брали маленькие простые карты, например, карта Мурманской области, потом Липецкой области с 18 районами, карта Московской области. Все эти карты мы раскрасили в 4 цвета, хотя это и получалось не с первого раза. Среди всех опробованных нами карт не нашлось ни одной, где бы нужно было использовать пятую краску. Мы узнали, что теорема четырех красок была доказана математиками в 1976 году при помощи компьютерной программы и была первой теоремой, доказанной при помощи компьютерного моделирования.

     Задача раскраски карты может быть формализована как задача раскраски вершин графа. И решается она, разумеется, гораздо более сложным способом, чем просто раскрашивание карт цветными карандашами. В этом году руководитель поставил перед нами задачу изучения математического алгоритма решения этой задачи, что мы и сделали в этом году. Нами был изучен жадный алгоритм раскраски вершин графов, при помощи которого теперь мы можем раскрашивать карты, представленные в виде графов. Применение жадного алгоритма не всегда дает наименьшее количество цветов раскраски. Однако, существенно облегчает раскраску графов. Мы узнали, что карты могут быть представлены в виде планарных графов. И для любого планарного графа возможно раскраска в 4 или менее цветов. А вот выяснить какое минимальное количество цветов необходимо, чтобы раскрасить какой-то произвольный граф – сложная вычислительная задача. И решать ее за разумное время математики пока не умеют. Жадный алгоритм позволяет решать эту задачу быстро, но не дает точный ответ. Например, наши эксперименты с использованием различного порядка обхода вершин графа, показали, что в этом случае мы можем получить различное количество цветов вершин.

     Задача раскраски графов имеет и очень интересные практические приложения, что и определяет ее актуальность. Некоторые из них мы рассматриваем в своей работе. Например, задача распределения кроликов по клеткам. Как распределить кроликов по клеткам если они имеют предпочтения (какой кролик с каким не хочет быть в одной клетке). Эту задачу мы рассмотрели на примере распределение животных в зоопарке по клеткам. Вторая задача – задача назначения частот базовым станциям сотовой связи. Нельзя допустить ситуацию, когда две базовые станции находятся в близкорасположенных точках и работают на одной частоте, так как в этом случае не избежать помех. Мы рассмотрели пример на основе карты базовых станций Билайна города Москвы. Соединили ребрами те станции, которые распложены близко друг к другу и провели раскраску вершин графа (базовых станций ) и назначили им разные частоты.

            Итогом исследования является применение жадного алгоритма к решению двух практических задач: распределения кроликов по клеткам и назначения частот базовым станциям сотовой связи.

Исследование опирается на следующие библиографические источники:

1. Four, five, and six color theorems [Электронный ресурс]. Режим доступа: https://natureofmathematics.wordpress.com/lecture-notes/four-and-five-color-theorems/
2. Теория случайных графов. Интервью с А. Райгородским, д. ф.-м. н., проф. МГУ и МФТИ [Электронный ресурс]. Режим доступа: http://habrahabr.ru/company/postnauka/blog/201416/
3. Л.Ю.Березина. Графы и их применение: Популярная книга для школьников и преподавателей. Изд.стереотип.– М.:Либроком, 2014.
4. Мартин Гарднер. Остров пяти красок. Martin Gardner. The Island Of Five Colours (Fantasia Mathematica, N.Y., 1958) [Электронный ресурс]. Режим доступа: http://lib.ru/INOFANT/GARDNER_M/island.txt

Исследования согласованности оценок на примере конкурса песни «Евровидение» и выборов старосты класса

Автор: Поляков Яков Александрович, Российская Федерация, г. Липецк, МБОУ СОШ 68 г. Липецк, 5 Б класс

Научный руководитель: Сысоев А.С., к.т.н., доцент кафедры прикладной математики Липецкого государственного технического университета

Аннотация работы
Важно или нет, согласованны ли мнения людей при выставлении оценок, голосовании, ранжировании чего-либо? Конечно, это очень важно. В том объеме информации, которая сегодня нас окружает, учесть это не всегда бывает просто, но возможно.

Посмотрев в этом году конкурс песни "Евровидение", я подумал, а отчего зависит, победит ли песня или нет? От ее качества, известности исполнителя или чего-то еще? Может быть все дело в том, кто с кем граничит? В любом случае, голосуя, делают ли это страны согласованно?

А потом я подумал - выборы старосты в классе - это ведь точно такой же процесс выставления оценок претендентам. А что, если учесть согласованность выставления оценок, чтобы доказать одноклассникам, есть ли четкий лидер в классе или все претенденты достойны быть старостой?

Целью работы является оценка согласованности данных, полученных в двух ситуациях. Во-первых, оценка согласованности мнений стран-участниц конкурса песни "Евровидение - 2015", а во-вторых, оценка согласованности мнений школьников при выборе старосты класса.

Задачи

1. Выяснить, что такое согласованность данных, как она измеряется.
2. Провести анализ согласованности баллов, выставленных участникам конкурса песни «Евровидение - 2015».
3. Используя полученный опыт, произвести оценку согласованности результатов выборов старосты класса.

Методы, используемые в работе: методы математической статистики, методы экспертных оценок.

Основной текст тезисов

Давайте представим себе ситуацию, когда необходимо подтвердить или опровергнуть правоту какого-либо человека или свершившегося факта. Например, при оценке качества интересующего нас продукта или изделия специалистами - добросовестно и беспристрастно подошли ли они к своей работе? Назовем эту оценку исследуемым признаком. Решают задачи, в которых оцениваются значения признака у ряда явлений, процессов или людей. Множество объектов, значения признака которых оценивается, называется множеством факторов. И мы подошли к последнему главному вопросу - кто будет оценивать? Это группа людей, которых называют экспертами. Итак, эксперты выставляют оценки по факторам. В результате получается таблица значений. Задача оценки согласованности данных состоит в том, чтобы с помощью анализа некоторых расчетных математических показателей сказать, едины ли в своем решении были эксперты или нет. То есть, получаем ответ на вопрос - является ли принятое решение мнением большинства. В случае, когда оценок немного, то сделать это легко и без использования математики. Но чаще бывает, когда оценок много и визуальный анализ ни к чему хорошему нас не приведет. Для оценки согласованности данных используется коэффициент ранговой корреляции или конкордации (от франц. concorde - согласие). Коэффициент конкордации отражает степень согласованности мнений экспертов по всем характеристикам. В нашем исследовании мы установили степень согласованности мнений экспертов при выборе стран-победителей на конкурсе Евровидение и при выборе старосты класса. Нами были получены следующие результаты:

1. При анализе согласованности результатов голосования в финале конкурса песни "Евровидения" получили умеренную согласованность. Это говорит, с одном стороны, о том, что страны, оказавшиеся наверху турнирной таблицы действительно достойны этого, и большинство экспертов это подтверждают, а с другой стороны - выставление более низких оценок обусловлено случайными факторами, такими как локальные предпочтения или сложившаяся политическая ситуация.
2. При анализе оценок претендентам на должность старосты класса получили слабую согласованность. Это говорит о том, что все соперники практически в равной степени достойны быть старостой нашего класса.

Итогом исследования является применение математических методов для решения практических задач по определению степени согласованности мнений экспертов, что можно использовать в самых различных областях жизнедеятельности человека.

Исследования опираются на литературные источники:

1. Ковалева Т.Ю. Практикум по теории статистики. М.: «КноРус», 2012. - 376 с.
2. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. Методы обработки данных. Пер. с англ. - М.: Мир, 1980. - 620 с.
3. Макаров И.М., Виноградская Т.М., Рубчинский А.А. Теория выбора и принятия решений. М.: Наука, 1982. — 328 с.
4. Eurovision Song Contest. http://www.eurovision.tv/page/timeline

Графы с цветными рёбрами и их интерпретация с помощью чисел Рамсея

Зубрилина Софья Феликсовна

Россия, Липецкая область, г. Липецк

МБОУ лицей №66, ЦДО “Стратегия”, 8 класс

Научны руководитель к.т.н., доц.кафедры прикладной математики Липецкого государственного технического университета Шуйкова И.А.

Целью работы является изучение алгоритмов реберной раскраски графов, их прикладного назначения и программная реализация указанных алгоритмов.

В ходе исследования были поставлены и решены следующие задачи:

1. изучение графов и их основных свойств, составление списка литературы;
2. изучение алгоритмов реберной раскраски графов и оценка их сложности;
3. рассмотрение прикладных задач, которые формализуются при помощи графов;
4. изучение чисел Рамсея, позволяющие интерпретировать графы с цветными ребрами;
5. программная реализация жадного алгоритма реберной раскраски двудольного графа;
6. анализ свойств реализованного алгоритма.

В данной работе рассматриваются основные понятия графов; изучаются графы с цветными рёбрами, правильная раскраска двудольного графа и графы, рёбра которых раскрашены в два цвета. Известно, что не существует точного полиномиального алгоритма реберной раскраски, однако есть менее точные жадные алгоритмы, позволяющие получить хорошее приближение по классам разбиения цветных ребер к точной оценке. В работе предлагается программная реализация жадного алгоритма для произвольного двудольного графа.

Актуальность данного исследование заключается в том, что многие задачи, такие как составление расписаний, выбор оптимального распределения, расписания в круговых турнирах и многие другие, формализуются с помощью графов и могут быть решены рассматриваемыми в работе алгоритмами рёберной раскраски графа.

Практической основой данной работы послужила проблема составления расписания для  «Дня Здоровья», проводимого во всех поликлиниках города. В этот день приглашают квалифицированных врачей из других городов. И все жители могут проконсультироваться у них. Но необходимо решить проблему приёма пациентов, так как создать “живую” очередь в поликлинике будет очень неудобно. Я предлагаю своё решение этой задачи, которое будет опираться на жадный алгоритмы рёберной раскраски графов.

В работе предлагается программная реализация одного из жадных алгоритмов для правильной рёберной раскраски двудольного графа. Также в работе изучается теорема Рамсея и числа Рамсея, интерпретация графов с их помощью. В ходе исследования создана программная генерация некоторых графов, обладающих свойством Рамсея.

В результате проделанной работы были сформулированы следующие выводы:

1. Изучены алгоритмы реберной раскраски графов, создана программная реализация одного из алгоритмов.
2. Изучены графы и их некоторые основные свойства.
3. Изучены алгоритмы рёберной раскраски и их свойства, произведена оценка сложности и время работы алгоритма.
4. Рассмотрены прикладные задачи, которые формализуются при помощи графов.
5. Решена практическая задача “Дне Здоровья”.
6. Изучены числа Рамсея, позволяющие интерпретировать графы с цветными ребрами.

Исследование опирается на следующие библиографические источники:

1. Асанов М., Баранский В., Расин В. — Дискретная математика: Графы, матроиды, алгоритмы — СПб.: Издательство "Лань", 2010. — 291 стр.
2. Шикин Е. В., Чхартишвили А. Г. Математические методы и модели управлений: Учеб. Пособие. – М.: Дело, 2000.
3. Березина Л. Ю. Графы и их применение.: Популярная книга для школьников и преподавателей. Изд. стереотип. - М.: Книжный дом  “ЛИБРОКОМ ”, 2014.
4. Дискретная математика для программистов / Ф. А. Новиков – СПб:  Питер, 

Исследовательский проект: "Комбинаторные задачи. Анализ решения при помощи рекуррентных соотношений и производящих функций"

Первеев Михаил

МАУ ДО ЦДО "Стратегия" и МБОУ СОШ №2 г.Липецка

Шуйкова Инесса Анатольевна, к.т.н., доц. кафедры прикладной математики ЛГТУ

Целью работы является систематизация комбинаторных объектов и сравнительный анализ решения комбинаторных задач при помощи рекуррентных соотношений и производящих функций.

Методы, используемые в работе: методы дискретной математики и теории производящих функций.

Актуальность работы: комбинаторные объекты не только применяются для решения широкого круга задач, но необходимы для разложения в ряд многих “классических функций” – их коэффициенты имеют комбинаторную интерпретацию. Поэтому в своей работе я не только систематизировал комбинаторные объекты – описал формулы, написал компьютерную программу для генерации комбинаторных объектов, но и рассмотрел производящие функции. Теория производящих функций позволяет решать такого рода задачи компактно, лаконично, используя красивый и убедительный математический аппарат.

Описание научно-исследовательской работы: в предлагаемой работе рассматриваются методы решения комбинаторных задач: при помощи их рекуррентное представления и решения рекуррентных соотношений и с использованием производящих функций. Рассматриваются решения задач: “Числа Фибоначчи”, “Размен”, “Счастливые билеты” двумя методами. Реализована компьютерная программа, генерирующая комбинаторные объекты.

Выводы: в ходе исследования были поставлены и решены следующие задачи: изучена литература по теме исследования, разобраны производящие функции и решены с их помощью задачи, которые предварительно решены с помощью рекуррентных соотношений. Разработана компьютерная программа, позволяющая вычислить всевозможные характеристики различных комбинаторных объектов. В дальнейших работах планируется решить свою собственную прикладную задача двумя методами и произвести расширение функционального наполнения программы и вывод производящих функций для всех представленных комбинаторных объектов.

Библиографический список: 

1. Виленкин Н.Я. Популярная комбинаторика. – М.: “Наука”, 1975.
2. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики. – М.: “Мир”, 1998.
3. Костюкова Н.И. Основы информационных технологий. Графы и их применение. Комбинаторные алгоритмы для программистов. – М.: “БИНОМ. Лаборатория знаний”, 2007.
4. Ландо С.К. Введение в дискретную математику. – М.: МЦНМО, 2012.
5. Сайт алгоритмов и программ [Электронный ресурс] // MAXimal. URL: http://e-maxx.ru/
6. Сайт о производящих функциях последовательностей [Электронный ресурс] // Производящие функции 2010. URL: http://genfunc.ru/

Исследовательский проект: "Экстремальные свойства Платоновых тел, ограниченных правильными треугольниками."

Советников Тимофей Олегович

Муниципальное автономное образовательное учреждение лицей №18 г. Калининград

Малаховский Николай Владиславович, к.ф.-м.н., доцент кафедры естественнонаучных и технических дисциплин Московского государственного университета технологии и управления (Калининградский филиал)

 Цели и задачи:

Научная работа посвящена изучению экстремальных свойствами правильных пирамид. Выражением этих экстремальных свойств являются определённые оценки, справедливые для правильных пирамид с любым числом боковых граней, но которые достигаются только в случае правильных пирамид, у которых все рёбра равны между собой с числом сторон правильного многоугольника, являющегося её основанием, равным 3,4 и 5.

Актуальность, значимость и новизна:

В естественных науках встречаются многие правильные тела, но особое значение имеют правильные многогранники с треугольными гранями тетраэдр, октаэдр и икосаэдр. Например, в структурной химии координационный полиэдр с треугольными гранями представляет собой наиболее компактное расположение соседних атомов, кроме этого существуют и другие причины широкой распространенности тетраэдрической н октаэндрической координации. Икосаэдрическая координация обнаружена в многочисленных структурах сплавов. По вершинам икосаэдра, например, расположены 12 связанных с металлом кислородных атомов в ионе Се(МОз)о3 и карбонильные группы в Fe3(CO)i2 и Со4(СО). Икосаэдрнческие группы присутствуют в элементном боре и некоторых борндах. Кроме того, из икосаэдров или из их частей построен макет, состоящий из атомов бора, во многих боранах. Возникает вопрос об особенной значимости именно тех Платоновых тел, гранями которых являются правильные треугольники. В научной работе этот феномен объясняется экстремальными свойствами правильных пирамид с равными рёбрами, порождающих эти тела.

Итоги исследования

В научной работе феномен особой значимости Платоновых тел, гранями которых являются правильные треугольники, естественных науках объясняется экстремальными свойствами правильных пирамид с равными рёбрами, порождающих эти тела.

Список использованной литературы:

1. Александров А.Д. Выпуклые многогранники. – М.-Л.; 1950.
2. Долбилин Н.П. Жемчужины теории многогранников. – М.: МЦНМО, 2000, с.27-31.
3. Люстерник Л.А. Выпуклые фигуры и многогранники. – М.; 1956.
4. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949, с. 34, с.268.
5. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.
6. Яглом И.М., Болтянский В.Г. Выпуклые фигуры. – М.-Л.; 1951 /Библиотека математического кружка, выпуск 4.

Исследовательский проект: "Пространства квадратов Дюрера"

 Карбышева Анастасия Александровна

Муниципальное автономное образовательное учреждение лицей №18 г. Калининград

Научный руководитель: Малаховский Николай Владиславович, к.ф.-м.н., доцент кафедры естественнонаучных и технических дисциплин Московского государственного университета технологии и управления (Калининградский филиал)

Цели и задачи:

 Целью научной работы является изучение векторных и аффинных пространств и подпространств, порождаемых оригинальным квадратом Дюрера, метрической геометрии и определителей квадратов Дюрера, а также определителей пандиагональных квадратов, собственных векторов и собственных значений оригинального квадрата Дюрера.

Актуальность и новизна исследования:

 Теория магических квадратов прошла долгий и сложный путь развития. В XIX и XX веках интерес к магическим квадратам вспыхнул с новой силой. Они нашли своё применение в криптографии и приборостроении. Особое место в теории магических квадратов занимает разработка методов их построения. Магические квадраты могут быть применены в криптографии. Они позволяют создать алгоритм перевода зашифрованного текста в изображение и, наоборот. Магические квадраты применяются в технологиях создания телевизоров, что позволяет обеспечить плавные цветовые переходы, полностью устраняя видимые границы на больших однотонных полях изображения.

Описание научно-исследовательской работы:
В научной работе рассматриваются пространства и подпространства, порождаемые магическими квадратами Дюрера. На множестве всех квадратов Дюрера вводятся операции сложения и умножения квадрата Дюрера на действительное число. Доказывается, что множество всех квадратов Дюрера обладает структурой семимерного векторного пространства D над множеством всех действительных чисел , так как в результате этих операций сохраняются магические свойства этих квадратов. Определяется аффинное подпространство(D) пространства D. Рассматривается пятимерное векторное подпространство P пространства D пандиагональных квадратов. Проводятся метрические исследования в подпространствах (D) and P.

Итоги исследования:

 Используя методы линейной алгебры в работе получен ряд новых научных результатов по теории магических квадратов Дюрера В частности, рассмотрены пространства и подпространства, порождаемые магическими квадратами Дюрера. На множестве всех квадратов Дюрера введены операции сложения и умножения квадрата Дюрера на действительное число. Доказано,  что множество всех квадратов Дюрера обладает структурой семимерного векторного пространства D над множеством всех действительных чисел . Определено аффинное подпространство(D) пространства D. Рассмотрено пятимерное векторное подпространство P пространства D пандиагональных квадратов. Проведены метрические исследования в подпространствах (D) and P.

Список использованной литературы:

1. Я. В. Успенский. Избранные математические развлечения.- Сеятель, 1924.
2. Б. А. Кордемский. Математическая смекалка.- М.: ГИФМЛ, 1958.- 576с.
3. М. М. Постников. Магические квадраты.- М.: Наука, 1964.
4. Н. М. Рудин. От магического квадрата к шахматам.- М.: Физкультура и спорт, 1969.
5. Е. Я. Гуревич. Тайна древнего талисмана.- М.: Наука, 1969.
6. М. Гарднер. Математические досуги.- М.: Мир, 1972.
7. Ю. В. Чебраков. Магические квадраты. Теория чисел, алгебра, комбинаторный анализ.- СПб.: СПб гос. техн. ун-т, 1995.
8. Ю. В. Чебраков. Теория магических матриц.- СПб., 2008.
9. М. Гарднер. Глава 17. Магические квадраты и куб.

Исследовательский проект:"Семейства героновых треугольников"

Сизых Артём Константинович

Муниципальное автономное образовательное учреждение лицей №18 г. Калининград

Малаховский Николай Владиславович, к.ф.-м.н., доцент кафедры естественнонаучных и технических дисциплин Московского государственного университета технологии и управления (Калининградский филиал)

Краткая постановка цели и задач исследования:

Целью научной работы является определение однопараметрического семейства, порождающего все известные классы героновых треугольников. Используя таблицу - семейств героновых треугольников расширена известная классификация таких треугольников.

Актуальность, значимость и новизна, итоги исследования:

Используя таблицу $\lambda$- семейств героновых треугольников решены следующие задачи: определены все героновы треугольники в которых периметр равен площади, найдены все пары героновых треугольников с равными периметрами, найдены все пары героновых треугольников с равными площадями, определены все героновы треугольники, в которых периметр и площадь являются квадратами заданных чисел.

Полученные в научной работе семейства героновых треугольников позволяют не только провести классификацию всех известных типов героновых треугольников, но и определить новые не рассмотренные в научной литературе классы таких треугольников. Например, героновы треугольники, в которых периметр равен площади, пары героновых треугольников с равными периметрами, пары героновых треугольников с равными площадями, героновы треугольники в которых периметр и площадь являются квадратами заданных чисел.

В результате научного исследования решены следующие задачи:

1. сформулирована и доказана теорема, определяющая однопараметрические $\lambda$ - семейства героновых треугольников;
2. проведена классификация героновых треугольников, соответствующих различным значениям параметра ;
3. используя таблицу $\lambda$ - семейств героновых треугольников расширена известная классификация героновых треугольников.

Список использованной литературы:

1. Бухштаб А.А., теория чисел, М., Наука, 1967
2. Кордемский Б. Формулы, производящие героновы триады. ЗС // МВШ, 1984, № 4.
3. Люберанский А. И. Что можно узнать из формулы Герона?// Математика в школе. – 1998. – №6. – с.55–56.
4. Еременко С.Б., Сохет А.М., Ушаков В.Г. Элементы геометрии в задачах. – М.:МЦНМО.2003.

Исследовательский проект: "Обобщение формулы Декарта на n- мерное евклидовое пространство ".
 Терентьев Александр Денисович 
 Муниципальное образовательное учреждение лицей №18 г. Калининград 
 Малаховский Николай Владиславович, к.ф.-м.н., доцент кафедры естественнонаучных и технических дисциплин Московского государственного университета технологии и управления (Калининградский филиал) 

 Цели и задачи:

 целями научной работы являются обобщения теоремы Декарта на случай n- мерного Евклидова пространства и её применение к задачам трёх мерного евклидова пространства. Решение поставленной задачи осуществляется методами линейной алгебры и математического анализа. 

Актуальность и новизна исследования:

актуальность исследования заключается в том, что до этого не были рассчитаны максимальное количество сфер в цепи для Теоремы Декарта для 3-мерного Евклидова пространства и средняя погрешность в радиусах этих сфер.

Описание научно-исследовательской работы:

работа начинается с исторической справки, дальше методами линейной алгебры и математического анализа выведена и доказана Обобщённая теорема Декарта для 3-мерного и n-мерного Евклидова пространств, а так же расчёт средней погрешности сфер в цепи для 3-мерного пространства.

Итоги исследования:

в ходе работы была выведена Обобщённая теорема Декарта для n-мерного Евклидова пространства, были рассчитаны максимальное количество сфер в цепи для Теоремы Декарта для 3-мерного Евклидова пространства и средняя погрешность в радиусах этих сфер.

Список использованной литературы:

1. Учебник 10-11 класса «Алгебра и начало анализа» 
2. Курош А. Г «Курс высшей алгебры» 
3. Р.Декарт «Рассуждение о методе» 
4. Р.Декарт «Геометрия» 
5. Р.Декарт «Правила для руководства ума» 
6. Ресурсы интернет

Исследовательский проект:"Стереометрический аналог теоремы Пифагора "
Кормилицина Александра Сергеевна
Муниципальное образовательное учреждение лицей №18 г. Калининград
Научный руководитель: Малаховский Николай Владиславович, к.ф.-м.н., доцент кафедры естественнонаучных и технических дисциплин Московского государственного университета технологии и управления (Калининградский филиал) 

Целью научной работы является доказательства факта, что множество вершин невырожденных пифаго-ровых тетраэдров никогда не определяет сферу, а принадлежит эллипсоиду (в отличие от окружности в случае пифагоровых треугольников). В случае неравностороннего треугольника оси эллипса, обра-зованного сечением эллипсоида плоскостью обладают экстремальными свойствами.

Описание научно-исследовательской работы:

В научной работе рассмотрено одно из обобщений теоремы Фалеса на случай трёхмерного пространства и доказано, что в этом случае теорема не верна.

Актуальность, значимость и новизна исследования:

Анализ философской, психолого-педагогической и математико-методической литературы, опыта работы преподавателей математики показал, что методическое значение обобщений как средства обучения математике достаточно велико и разнообразно. Обобщения являются средством и способом введения и определения многих математических понятий, формулировок теорем, средством и методом доказательства различных теорем, решения и обучения решению большого числа математических задач Обобщения также могут быть источником новых математических задач. Однако, в некоторых случаях формальные обобщения теорем и формул могут приводить к фундаментальным ошибкам.

Итоги исследования:

В результате обобщения теоремы Пифагора на трёхмерное пространство доказано, что вершины пифа-горовых тетраэдров никогда не определяют сферу, а принадлежат эллипсо-иду, две главные оси кото-рого обладают экстремальными свойствами.

Список использованной литературы:

1. Скопец З. А. Геометрические миниатюры, М. Просвещение,1990
2. Еленьский Щ. По следам Пифагора. М. Просвещение, 1961
3. Глейзер Г. И. История математики в школе. М. Просвещение, 1982
4. Литцман В., «Теорема Пифагора» М. Просвещение, 1960.

В работе рассматривается вопрос поиска результативных,схожих с исходным, уравнений, также имеющих решения (согласно условиям, представленным в первоисточнике), дан исчерпывающий, обобщающий ответ на поставленный вопрос, проведена статистика численных значений левых, а, значит, и правых частей получаемых равенств. 

Исследовательский проект:"Обобщение теоремы Пифагора на правильные  n- угольники"

  Мариевский Никита Андреевич.

  Муниципальное автономное образовательное учреждение лицей №18 г. Калининград.

  Малаховский Николай Владиславович, к.ф.-м.н., доцент кафедры естественнонаучных и   технических дисциплин Московского государственного университета технологии и управления (Калининградский филиал).

Краткая потановка цели и задач исселедования:

  Получить обобщение теоремы Пифагора, в котором рассматриваются треугольники, на сторонах которых (или на сумме двух сторон) во внешнюю (или во внутреннюю стороны) строятся правильные n-угольники, площадь одного из которых равна площади сумме двух остальных, измеряемых в единицах площадей правильных  n-угольников. 

Описание научно-исследовательской работы:

В научно-исследовательской работе определяется зависимость площади,измеряемой в квадратных единицах, от площади, измеряемой в n-ных единицах, откуда получается вывод, что коэффициент пропорциональности не зависит от длин сторон многоугольника.

Актуальность, значимость и новизна исследования:

Теорема Пифагора играет в геометрии исключительную роль. На ней основано применение в евклидовой геометрии метода координат, который позволяет привнести в геометрию алгебраические методы. Отказываясь от тех или иных условий, можно получать различные обобщения теоремы Пифагора, которые позволяют взглянуть на неё с неожиданной стороны.

Итоги исследования:

Получена связь между обычной площадью (в квадратных единицах) правильного n-угольника со стороной a+b и той же самой площадью, выражаемая в новых единицах.Доказана теорема:  площадь правильного n-угольника со стороной a+b равна сумме n площадей треугольника  и площади правильного n-угольника со стороной равной смежной гипотенузе (соответственно гипотенузе). Теорему можно рассматривать как n-ный аналог теоремы Пифагора, поскольку в теореме Пифагора единицей измерения площади является площадь квадрата со стороной равной единице длины, соответственно для n-ного аналога теоремы Пифагора единицей измерения площади естественно считать площадь правильного n-угольника со стороной равной единице длины.

Список использованной литературы:

1. Скопец З. А. Геометрические миниатюры, М. Просвещение,1990
2. Еленьский Щ. По следам Пифагора. М. Просвещение, 1961
3. Глейзер Г. И. История математики в школе. М. Просвещение, 1982
4. Литцман В., «Теорема Пифагора» М. Просвещение, 1960.

Файл читается в документе word.

Информационно – моделирующая программа «Моделирование броска тела под углом к горизонту»

Молчанов Иван Витальевич  ученик 11 «А» класса, ГУО «Гимназия №1 г. Бреста».

Краткое описание

Данный проект является универсальной информационно – моделирующей системой для изучения темы «Моделирование броска тела под углом к горизонту» из курса физики.

Проект состоит из трёх частей: основной клиентской «Информационно-тестирующей части», «Редактора заданий теста» и серверной части «Сервера».

Информационно-тестирующая часть – запускаемый файл MyGL.exe

Главное окно программы содержит закладки, соответствующие основным её пяти разделам: «Старт», «Теория», «Модель», «Тест», «Отчёт».

Раздел «Старт» содержит название программы и раздел регистрации пользователя. Регистрацию необходимо пройти, если будет осуществляться тестирование с отправкой результатов на сервер. После заполнения всех полей формы регистрации надо нажать кнопку «Подтвердить». Если связь с сервером не предполагается, то регистрацию можно пропустить, нажав кнопку «Игнорировать».

Раздел «Теория» содержит теоретическую информацию по соответствующей теме. В этом разделе организована возможность просмотра множества страниц и их нумерация.

Раздел «Модель» является основным и позволяет произвести моделирование полёта тела, брошенного под углом к горизонту. Модель является визуальной и динамической.

Раздел «Тест» позволяет пройти тест по соответствующей теме. Запуск теста производится нажатием на кнопку «Начать тестирование».

Раздел «Отчёт» содержит подробные результаты выполнения теста. А именно, количество правильных ответов, оценку, а также таблицу с результатами ответов по каждому вопросу.

 Редактора заданий теста – запускаемый файл Redactor.exe. Главное окно программы содержит закладки, соответствующие основным её двум разделам: «Часть А» и «Часть В». Редактора заданий теста позволяет вводить текст вопроса, варианты ответов и правильный ответ. Каждый вопрос и варианты ответа сохраняются в файле, содержание которого шифруется. Впоследствии, при использовании вопроса при тестировании варианты ответов переставляются случайным образом.

 Сервер – запускаемый файл Server.exe. Должен быть запущен на компьютере учителя. Имеются две кнопки, включающие и отключающие сервер и таблица, в которой будут отображаться результаты тестирования учащихся, передаваемые с компьютеров-клиентов по локальной сети.

Петер Густав Лежен Дирихле и его принцип.

Исполнитель: Довга Денисия Кемаловна, Ревунова Дарья Дмитриевна, 8 класс

Руководитель: Калеганова Марина Валерьевна, Учитель математики первой категории

Автономное общеобразовательное учреждение Муниципального образования г. Долгопрудного средняя общеобразовательная школа №1 (АОУ школа №1) 

Наша работа касается одного из интересных эвристических методов решения математических задач - принципа Дирихле. Принцип назван в честь немецкого математика Петера Густава Лежена Дирихле (1805-1859 г.), который успешно применял его к доказательству арифметических утверждений.    

Целями работы являются следующие:

1. изучить, один из основных методов математики, принцип Дирихле.
2. Выявить круг задач, решение которых основывается на принципе Дирихле;

Задача: Научиться применять соответствующие формулировок принципа Дирихле – наиболее рациональный подход при решении задач.

Объектом нашего исследования является принцип Дирихле

Предметом нашего исследования является различные формулировки принципа Дирихле и их применение при решении задач.

Итоги исследовательской работы.

Петер Густав Лежен Дирихле –автор многих достижений в области математики, но одна из его важнейших заслуг – это формулировка логического приема доказательства, названного его именем. Принцип Дирихле применяется в разных разделах математики: в арифметике, в комбинаторике, в геометрии.  Этот принцип можно применять в повседневной жизни, что развивает логическое мышление.  

 В работе показана теоретическая значимость принципа Дирихле как основного метода формирования теории чисел. Подтверждена практическая значимость неконструктивного доказательства, которое лежит в основе этого принципа. Приведены исторические сведения, формулировка принципа Дирихле и задачи.

Многие олимпиадные задачи решаются, используя это специальный метод.

Дирихле – автор многих достижений в области математики, одна из его важнейших заслуг - это логический прием доказательства, названный его именем.

Актуальность его работы несомненна, хотя бы потому, что знакомство с новыми методами решения задач расширяет круг людей.

Список используемой литературы

1. http://mirznanii.com/info/id-85
2. https://ru.coursera.org/learn/teoriya-grafov/lecture/lpD8n/nachalo-dokazatiel-stva-primienieniie-printsipa-dirikhlie
3. http://www.problems.ru/articles/216.php
4. https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%94%D0%B8%D1%80%D0%B8%D1%85%D0%BB%D0%B5_(%D0%BA%D0%BE%D0%BC%D0%B1%D0%B8%D0%BD%D0%B0%D1%82%D0%BE%D1%80%D0%B8%D0%BA%D0%B0)
5. https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%94%D0%B8%D1%80%D0%B8%D1%85%D0%BB%D0%B5
6. https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%94%D0%B8%D1%80%D0%B8%D1%85%D0%BB%D0%B5_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0)
7. http://math4school.ru/princip_Dirihle.html
8. http://www.kvant.info/spivak67/archiv/19992000/spivak67/s_diri.htm
9. http://ermine.narod.ru/MATH/STAT/DIRIHLET/sect1.htm
10. http://math4school.ru/princip_Dirihle.html

1) Физика. Обучающая и тестирующая система

2) Заводов Андрей Павлович

3) МОУ Лицей №43, г. Саранск

4) Виктор Иванович Ивлев, Профессор кафедры физики твердого тела МГУ им. Огарева

5) Цели и задачи:

• Упрощение изучения физических определений
• Оптимизация тестирования и проверки школьных работ.
• Закрепление пройденного материала, методом тестирования.
• Возможность писать развернутые ответы на вопросы.

6) Физика. Обучающая и тестирующая система - приложение, позволяющее в удобной форме изучать все термины из школьного курса физики.

Определения рассортированы по разделам для более удобного восприятия. Также присутствует поиск, который быстро найдет все совпадения по запросу.

По каждому из разделов вы можете пройти тестирование, причем без выбора варианта ответа, а написав свое собственное определение. Алгоритм сравнения проанализирует ваш ответ и выдаст вердикт: на сколько процентов ваш ответ совпадает с правильным и можно ли считать его верным.

В новой версии добавлены новые возможности тестирования: вставка пропущенных слов в определения или тестирования с вариантами ответа.

Помимо всего есть возможность составлять свои собственные тесты, в которые можно добавлять вопросы из базы данных или свои собственные. Программа шифрует все результаты, поэтому подделать их не получится. Итоги тестирования вы можете расшифровать и посмотреть только в самой программе.

Особенности Физика. Обучающая и тестирующая система:

• База данных содержит 460 определений.
• 3 варианта тестирования: развернутый ответ, выбор правильного варианта, вставка пропущенных слов
• Возможность самим создавать и настраивать тесты
• Можно одновременно сравнивать несколько результатов.
• Все результаты шифруются.
• Вы можете сами настроить шрифт и размер текста.

7) Постоянно возрастает потребность в тестировании и быстрой проверки работ. Но до сих пор нет системы, которая анализирует и проверяет работы со свободной формой записи ответов.

8) Моя программа учитывает падежи, наличие и отсутствие слов, наличие и отсутствие лишних слов, а также словосочетания и порядок постановки слов в ответе. Опираясь на все эти данные, она выдает совпадение текстов в процентном соотношении, что дает возможность проводить тестирование с развернутым ответом.

9) После долгого редактирования и подгонки конечной формулы, удалось вывести оптимальный (на данный момент) вариант оценки работ.

8-ая международная конференция научно-технических работ школьников «Старт в Науку»

Название научно-исследовательской работы: «Компьютерное моделирование загрязнений атмосферы».

ФИО автора работы: Балезин Олег Александрович, 22.09.2000.

Образовательное учреждение, в котором обучается автор работы: ученик 9  класса МАОУ «Лицей №102 г. Челябинска»

ФИО, должность и место работы научного руководителя: Пашнин Андрей Александрович, педагог  дополнительного образования класса МАОУ «Лицей №102 г. Челябинска»

Краткая постановка цели и задач исследования.

Разработка программного комплекса способного моделировать устойчивую картину  распространения загрязнений в атмосфере.

Задачи проекта: Реализовать алгоритм  моделирования распространения загрязнения атмосферы c  использованием  клеточных автоматов.  Протестировать программу.

Основной текст тезисов. Краткое техническое описание проекта

Моделирование загрязнений производится с помощью алгоритмов клеточных автоматов. На реальной карте задается решетка. Определенные клетки являются загрязнителями со своим уровнем загрязнения. Задается  роза ветров в виде матрицы, которая определяет вероятность ветра по сторонам света. В программе  моделируется устойчивая  пространственная картина загрязнения  атмосферы . Чтобы визуализировать  результаты используется цветовая палитра, каждому уровню загрязнения соответствует свой цвет. В итоге получается цветовая картина загрязнений. Программа написана на языке  Java, который позволяет  формировать удобный интерфейс  и масштабировать задачу.

Актуальность исследования.

Состояние качества воздушной среды в городах в настоящее время является одной из острейших проблем современности. В большинстве городов мира загрязнение воздуха достигает критических размеров. По оценкам Всемирной организации здравоохранения (ВОЗ), показатели качества воздуха в 20 крупнейших городах мира в несколько раз превышают установленные ВОЗ нормативы. Более 1 млрд. горожан подвержены воздействию опасных для здоровья уровней загрязнения воздуха.

Значимость и новизна исследования.

При  планировании строительства новых предприятий необходимо иметь модель, способную оценить  возможное влияние данных  предприятий  на уровни загрязнений атмосферы.

Особенно это актуально при непосредственной близости  жилых  районов. Также важно иметь модель загрязнений атмосферы   уже существующих предприятий при планировании строительства новых жилых районов. Поэтому очень актуально наличие компьютерной  модели, позволяющей моделировать устойчивую картину загрязнения атмосферы.

Итоги исследования.

Решены сформулированные задачи проекта:

Реализован алгоритм клеточных автоматов для моделирования загрязнения атмосферы. Программа протестирована на различных конфигурациях. Алгоритм показал адекватные результаты: распространение загрязнений происходило по площадям эллиптической формы по направлению розы ветров.   

Перспективы проекта: Привязка данной программы к реальным компьютерным картам местности посредством функции API. Совершенствование интерфейса. Интеграция программного комплекса с системой датчиков загрязнений для оперативного моделирования.

НАУЧНЫЙ ПРОЕКТ НА ТЕМУ:

«ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ С ПОМОЩЬЮ ЛИНЕЙНОЙ И КВАДРАТИЧНОЙ ФУНКЦИЙ».

Исполнитель:

Рахимова  Мухиба Алишеровна - ученица 11 « В» класса, Президентского лицей - интерната для одаренных детей города Душанбе, Таджикистан.

Научный Руководитель:

Олимджони Пирахмад – учитель по подготовке школьников к олимпиадам по математике в  школе «Хотам и ПВ».

Введение

  В данной работе приведен метод доказательств нестандартных неравенств с помощью линейной и квадратичной функций. В неравенствах, которые доказываются с помощью линейной и квадратичной функций достаточно знать характер графика квадратичной функции. 

  Во многих сложных неравенствах можно использовать известные неравенства как неравенство между средним арифметическим и средним геометрическим (неравенство Гельдера и др.), а потом можно закончить доказательство с помощью метода предложенного  в данной работе. Многие неравенства имеют сложную траекторию решения.

  Приведенный в настоящей работе метод является простым и конкретным методом для решения этих задач.

Краткая постановка цели и задач исследования

   Целью научного проекта является доказательства неравенств с помощью линейной и квадратичной функции. Многие неравенства имеют сложную траекторию решения. Приведенный в настоящей работе метод является простым и конкретным методом для решения этих задач.

Заключение

  Этот проект включает в себя методы доказательств алгебраических неравенств с помощью линейной и квадратичных функций. До сих пор многие сложные (олимпиадные) неравенства не имеют конкретного и простого метода решений. Этот метод является конкретным и простым для решения многих сложных неравенств. Для использования такого метода для доказательства неравенств достаточно знать характер графика линейных и квадратичных функций. Как отмечено выше, во многих сложных неравенствах можно использовать упамянутые в проекте полезные леммы. А так же, во многих неравенствах можно использовать некоторые известные неравенства или какие-то преобразования с условиями, а потом этот метод. Многие неравенства имеют сложную траекторию решения. С помощью этого метода можно составить задачи для математических олимпиад или математических экзаменах. Для этого необходимо пройти с конца решения вышеупомянутых задач до какого-то результата.

Список использованной литературы

[1] Pham Van Thuan, Trieu Van Hung, Proving inequalities using linear functions, Mathematical Reflections 4 (2006).

[2] Vo Thanh Van, Bat Dang ThucSchurVa Phuong PhapDoi Bien P, Q, R.

[3] Titu Andrescu, Vasile Cirtoaje, Gabriel Dospinescu, MirceaLascu, Old and New Inequalities, Gil Publishing House, 2004.

[4] Vasile Cîrtoaje, Discrete Inequalities, Volume 1, Symmetric Polynomial Inequalities, Art Of  Problem Solving 2015.

[5] Vasile Cîrtoaje, Discrete Inequalities, Volume 2, Symmetric Rational Inequalities, Art Of  Problem Solving 2015.

Поиск выигрышных стратегий в математической игре «Гекс»

Ионова Марина Олеговна

ГБОУ гимназия г. Сызрани

 науч. рук. Константинова Ирина Альбертовна, учитель математики ГБОУ Гимназия г. Сызрани

Целью работы является поиск выигрышных стратегий для игры «Гекс» на полях разной размерности.

Основные задачи исследования: сбор и изучение информации о правилах и истории математической игры «Гекс», рассмотрение подходов классической и прикладной математики к вопросу о выигрыше в игре, составление алгоритмов для выигрыша в игре на полях разной размерности.

За окном XXI век, время научно-технического прогресса. Компьютерные технологии затронули почти все сферы жизни деятельности людей, в том числе и развитие ребенка. Сколько придумано современных развивающих игр, но не учтен тот факт, что выигрышные ходы и стратегии можно с легкостью найти в интернете. Невольно старшее поколение замечает, что старые и проверенные на собственном опыте игры оказываются более интеллектуальными и лучше развивают логическое мышление.

Игра «Hex» (Гекс) популярна среди школьников и студентов. Правила игры очень просты. Играют двое на четырехсторонней доске из правильных шестиугольников фишками двух цветов. Размеры  доски могут быть 4х4, 5x5, 6x6 и 7x7 шестиугольников. Две противоположные стороны доски объявляются «красными», две другие – «синими». Игроки по очереди выкладывают свои фишки. За каждым игроком закреплена пара сторон доски – одинаковых по цвету с его фишками. Цель каждого игрока – соединить связным путем свои стороны своими фишками.

На своем опыте убеждаешься, что игра довольно-таки занимательная, но тут же назревает вопрос: существуют ли выигрышные алгоритмы для обоих игроков?  Я поставила перед собой задачу, составить алгоритмы для выигрыша в игре на полях разной размерности (4х4, 5х5, 6х6, 7х7), для чего изучила литературу по данной теме, проанализировала логические основы поиска выигрышных комбинаций и рассмотрела подходы теоретической и прикладной математики к проблеме поиска выигрышной стратегии в игре.

Научные работы, направленные  на поиск выигрышных алгоритмов в математических играх, довольно популярны. Однако поиск выигрышных стратегий для игры в «Hex» ранее был не изучен или, по крайней мере, не опубликован, в этом и заключается новизна и актуальность данного исследования. 

Теоретическая значимость данного исследования заключается в том, что предложенные мною алгоритмы поиска выигрышных стратегий полностью обоснованы.

По результатам исследования составлены алгоритмы для выигрыша в игре на полях разностью 4х4, 5х5, 6х6 и 7х7 и применение их для решения условных задач в игре. Так же исследовательская работа имеет немало перcпективных оснований для развития данной игры, такие как разработка 3D версии игры или практическое применение результатов исследования в различных отраслях науки и техники. 

Литература

Садовский Л.Е., Садовский А.Л. Математика и спорт / Библиотечка «Квант» вып. 44 – М.: Наука, 1985. – 193 с.

Гекс. Свободная энциклопедия «Википедия». – URL: https://ru.wikipedia.org/wiki/Гекс

Научно-исследовательская работа

“Расчет количества путей в ориентированном графе”.

Автор: Рябцовский Кирилл Викторович

Школа № 4 7”В” класс г. Сергиев Посад Московской области

Научный руководитель: Машков Дмитрий Александрович

Заместитель начальника отдела сопровождения информационной безопасности Департамента безопасности “Россельхозбанк”.

Цель: разработать математическую модель и алгоритм реализации расчета количества путей в направленном графе и реализовать это в компьютерной программе.

Важность решения данной задачи определена как одна из интереснейших задач теории графов, так и тем, что имеются типовые задачи на ЕГЭ по информатике.

В результате проведенной работы разработана компьютерная программа, автоматически решающая данный класс задач. 

декабрь 2015

Цель данной работы: познакомиться с различными методами, позволяющими предъявить нужное замощение или доказать, что требуемое замощение невозможно.

            В задачи данной работы входит: проведение исследовательской работы при решении задач на замощения различных фигур фигурками полимино, применяя при этом раскраску, числа, группы Замощения Конвея, регулярные полимино, перебор.

            В пункте «Паркеты» мы иллюстрируем паркеты, придуманные нами как на плоскости, так и в пространстве, показываем, как с помощью параллельного переноса можно заполнить всю плоскость (всё пространство) данными фигурками, используя для доказательства возможности замощения теорию «Сравнения по модулю». В приложении рассматриваются задачи, составленные автором работы по выше названной теме и приводятся хорошо известные в литературе любопытные результаты «о невозможном и возможном замощении».

            В результате нашей исследовательской работы мы пришли к следующим выводам. Для доказательства невозможности замощения некоторой фигуры различными полимино можно применить:

1) нужную раскраску или определённое расположение чисел на фигуре и полимино;

2) необходимое условие для существования замощения, используя теорию групп;

3) необходимое и достаточное условие регулярности прямоугольного полимино.

            В целом работа носит творческий, исследовательский характер, сопровождается большим количеством рисунков и задач, составленных руководителем и автором данной работы.

Автор: Цветков Ростислав
Челябинская область, г. Челябинск, Муниципальное общеобразовательное учреждение лицей №11, класс 11
Научный руководитель: Замоздра Сергей Николаевич
Кандидат физико-математических наук, доцент, в должности профессора кафедры теоретической физики ЧелГУ.

Исследование последствий удара метеорита о лёд на воде

Внезапно и непрерывно на Землю падают различные космические тела, но все они в основном разрушаются в атмосфере. Небесные тела, имеющие размеры от одного до нескольких десятков метров, частично сгорают в атмосфере. Остатки этих тел, упавшие на поверхность Земли и образующиеся от них ударные волны могут вызвать существенные разрушения.
Целью нашей работы является предсказывание последствий удара метеорита. Это предсказание может быть выполнено с помощью компьютерного моделирования (преимущество данного метода – возможность широкого выбора параметров) и с помощью экспериментов (ограниченность параметров). Наша цель в этом году – создание компьютерной модели, которая будет наглядно демонстрировать момент падения метеорита в озеро, покрытое льдом.
Основные этапы: 
1)        Изучить основы метеоритики.
2)        Собрать экспериментальную установку для моделирования удара метеорита о водоем, покрытый льдом
3)        Создать компьютерную модель падения метеорита в водоем со льдом
4)        Обработать и проанализировать результаты
В прошлом году мы исследовали удар метеорита о лёд на воде с помощью натурной модели. В этом году мы продолжили эти исследования с помощью компьютерной модели. Метеорит, лёд и вода представлены как системы частиц. Каждая частица взаимодействует со всеми остальными частицами. Уравнения движения частиц решаются численно методом Эйлера для двухмерной модели, и методом Верле для трёхмерной модели. Программа написана на языке Pascal. В программе можно задать такие параметры как плотность среды, количество частиц, их массу и начальную скорость, толщину слоёв и т.д. Для метеорита можно задавать те же параметры, но отдельно от остальных частиц. Для графического представления результатов вычислений используется программа Gnuplot. Так как данные о положении частиц записываются блоками (один блок – это один момент времени), мы получаем последовательность кадров.
Актуальность работы: Созданная компьютерная модель универсальна и может использоваться не только в метеоритике, но и в других областях науки, где необходимо детально рассмотреть поведение материалов или среды под действием внешних сил. В нашей модели можно задавать любые параметры среды и материалов, а также любые условия.
Выводы:
Удалось при помощи компьютерного моделирования детально рассмотреть момент падения метеорита в озеро со льдом. Трехмерная модель оказалась реалистичней, чем двухмерная, несмотря на большее время расчета. Это связано с тем, что в двухмерной модели энергия от метеорита распространяется только в плоскости, а также потому, что в трёхмерной модели используется более продвинутый способ расчета новых координат частиц. Собранные данные позволяют доказать, что лед на воде гасит волну, которая образовалась при ударе метеорита. Сразу после удара волна имеет достаточно энергии, чтобы беспрепятственно ломать лед, однако при удалении от центра полыньи, амплитуда волны угасает, и чем дальше от центра, тем сложнее волне ломать лед. В данном случае лед выступает в роли гасителя удара. Компьютерное моделирование наглядно показало процессы, происходящие в момент падения метеорита в водоем со льдом. В будущих версиях программы планируется увеличить скорость расчетов и реалистичность модели путем добавления более точного расчета давления жидкости.
Литература

1. Астероидно-кометная опасность / под ред. А.Г. Сокольского. СПб.: ИТА РАН, 1996. 224с.
2. Бадюков, Д.Д. Фрагменты Челябинского метеоритного дождя: распределение по массам, размерам и возможная масса максимального фрагмента /Д.Д. Бадюков, А.Е. Дудоров //Геохимия. 2013. № 7. С. 642-646.
3. Бронштейн, В.А. Метеоры, метеориты, метеороиды / В.А. Бронштейн. М., 1987. 173с.
4. Дудоров, А.Е. Частота падения метеоритов / А.Е. Дудоров, О.В. Еретнова // Вестник Челябинского государственного университета. 2014. №1. Физика. Вып. 19. С. 58-67.
5. Катастрофические воздействия космических тел / под ред. В.В. Адушкина, И.В. Немчинова. М.: Академкнига, 2005.310 с.
6. Пустынский, В.В. Следы космических воздействий на Землю, сборник научных статей / под ред. А.Н. Дмитриева. Новосибирск, «Наука», Сибирское отделение, 1990. 212с.
7. Федынский, В. В. Метеоры / Лекции по астрономии
   Выпуск 4. Государственное издательство технико-теоретической литературы.
   Москва, 1956. 104с.

«MobiFast : разработка drag and drop CMS для создания мобильных версий сайтов без знания программирования»

Степаненко Артур Русланович ученик 11 класса, ГУО"Гимназия №56 г.Гомеля"

В 2015 году компания Google официально запустила систему Google Friendly. Теперь сайты, которые имеют мобильную версию для смартфонов, трафик с которых в Рунете составляет 30%,получают специальную отметку. В поисковой системе Google эти сайты индексируются лучше и получают некоторые привилегии. Хотя необходимость адаптировать свои сайты к экранам смартфонов возникла намного раньше, это событие подтолкнуло к оптимизации даже тех, кто до последнего не хотел этого делать. В интернете появились конструкторы гибридных приложений и сайтов с большим количеством копирайтов сервиса и рекламы. Другие же сделали ставку на платные тарифы. Но у данных сервисов есть один очень веский аргумент в защиту - они позволяют самостоятельно заниматься разработкой своего сайта людям без знания языков Web-программирования. Цель работы: максимальное облегчение разработки мобильных версий для владельцев сайтов, минимизирование их временных затрат. Актуальность темы: данная тема чрезвычайно актуальна как для владельцев сайтов, так и для пользователей, учитывая то, что доля мобильного трафика постоянно увеличивается и имеет дальнейшие тенденции к росту.

Задачи работы : 1. Разработать drag and drop CMS для создания мобильных версий сайтов без знания программирования. 2. Предусмотреть систему шаблонности. 3. Дать возможность пользователю редактировать исходный код. 4. Предусмотреть последующую компиляцию исходного кода в гибридные мобильные приложения на базе AngularJS.

1. Полное исследование функции. Применение знаний о свойствах функции к решению задач.
2. Автор работы: Головнева Виктория Владимировна
3. ГБОУ Лицей «МКШ им. В. Н. Челомея»
4. Тё Ольга Владимировна, учитель математики в ГБОУ Лицей «МКШ им. В.Н. Челомея»
5. В начале работы были поставлены цели:

• Определить уровень знаний учеников общеобразовательных школ темы «Исследование функции» путем тестирования на примере учеников школы №3 города Байконур.
• Проанализировать вариант ЕГЭ 2016 по математике и сделать вывод о количестве заданий, в которых необходимы знания о полном анализе функции, а так же свойств функции.
  Привести пример решения таких заданий.
  6. Первая часть работы посвящена определению уровня знаний темы «Функция. Графики функции. Полное исследование функции» у учеников общеобразовательных школ на примере учеников школы №3 города Байконур. Для этого вышеуказанным ученикам был предложен следующий тест.
  На основе результатов этого теста были сделаны выводы о необходимости создания альтернативного способа преподавания этой темы, а именно создания наглядного пособия с понятным объяснением.
  Затем был проанализирован вариант ЕГЭ 2016, сделан вывод о количестве заданий, для решения которых необходимы знания свойств функций.
  Были приведены примеры решения некоторых заданий с использованием знаний об исследовании функции.
  7. данная тема часто в ЕГЭ встречается, а ее объяснению в школьной программе отводится не так уж много времени и объяснение выполняется по старым образцам, сложным и непонятным языком. отсюда можно понять, что предложение альтернативного варианта преподавания данной темы, а так же приведение примера применения полученных знаний для решения задач.
  8. 
  1. Учебник "Алгебра и математический анализ" 10 класс, Н.Я.Виленкин - М.,1931. - 115 с.
  2. Педагогический словарь. — М.: Академия. Г. М. Коджаспирова, А. Ю. Коджаспиров. 2005.
  3. Учебник "Алгебра. 8 класс" Теляковский
  4. Учебник "Алгебра. 9 класс" Теляковский - М.,1931. - 26с.
  5. http://www.oksanochka.com/003/001/024.shtml[Электронный ресурс]
  6. http://www.mathprofi.ru/asimptoty_grafika_funkcii.html[Электронный ресурс]

Расчёт траектории движения горячего пятна в аккреционном диске чёрной дыры

Исполнители: Дёмин Георгий, Назаренко Александр

Образовательное учреждение: Лицей Информационных Технологий №1533

Научный руководитель: Сергей Викторович Репин, сотрудник ИКИ (Института Космических Исследований)

Цель данной работы заключается в создании модели видимого движение горячего пятна, движущегося по круговой орбите в поле керровской чёрной дыры. 
Продемонстрировать различие между привычной нам механикой Ньютона и 
ОТО. Выполнить моделирование в рамках ОТО, путем численного решения 
дифференциальных уравнений движения квантов, что позволит максимально точно продемонстрировать такие параметры, как время движения и энергию излучаемых квантов. 

Описание научно-исследовательской работы: Виртуальное проектирование, реализованное в предлагаемом проекте, позволяет не только проводить точное исследование в области физики, но и детально понять, что такое искривленное пространство вокруг чёрной дыры. Для этого предлагается игра "Попади в пятно",

задача которой состоит в том, чтобы из одного горячего пятна, движущегося по круговой орбите вокруг чёрной дыры, попасть лазерной пушкой в пятно, движущееся по другой круговой орбите, причем обе орбиты задаются пользователем,

а все движения моделируются в рамках механики ОТО.

Для построения видимой траектории горячего пятна необходимо 

вычислить большое количество траекторий квантов, излученных изотропно этим 

горячим пятном. Для численного решения дифференциальных уравнений 

движения квантов используется язык программирования Fortran для 

быстродействия. Язык C# используется для написания основного 

тела программы и визуализации. Одной из трудностей было совместное 

использование этих языков. Также существовала проблема 

быстродействия, которая была решена путем использования различных 

алгоритмов сортировки данных и их оптимального хранения. 

Для дополнительной опции понадобилось сделать вид от наблюдателя,

был придуман новый алгоритм пересчёта координат.

 Актуальность проекта обусловлена большим научным интересом к 

развитию моделей таких астрофизических объектов как аккреционные 

диски и черные дыры. Сами эти объекты находятся от нас на огромном 

расстоянии и для понимания происходящих там процессов необходимо 

численное моделирование наблюдательных эффектов общей теории 

относительности (ОТО).

 Итоги проделанной работы:

Разработана программа, позволяющая: 

• Генерировать видимые движения горячих 

пятен в аккреционном диске в рамках механики ОТО, 

используя большой набор параметров; 

• Оптимизировать данные для наибольшего быстродействия;  
• Игра " Попади в пятно " с модификациями; 
• Сохранять полученные модели в виде набора параметров, что позволяет 

хранить смоделированную орбиту в удобном и компактном виде и

быстро восстанавливать ее, не выполняя повторных вычислений. 

Список используемой литературы:

1. A.F. Zakharov, S. Repin, Astronomy Reports, 43, 705, 1999.
2. A.F. Zakharov, S. Repin, Astronomy Reports, 46, 360, 2002.  
3. L.R. Petzold, SIAM Journal of Sci. Stat. Comput., 4, 136, 1983. 
4. Л.Д. Ландау, Е.М. Лифшиц. Теория поля, М., Физматлит, 2003. - 536  
5. Д.С. Литвинцева. Дипломная работа в лицее 1533, 2014 г.

   Работа выполнена учеником 10 класса МБОУ Лицея №40 Малышевым Артемом Андреевичем.

Научный руководитель: Овсянников Роман Ильич кандидат физико-математических наук н.с. 380 отд. ИПФ РАН

Актуальность темы: Полноразмерные расчёты молекулярных спектров являются громоздкими и требовательными к вычислительным ресурсам. Поэтому актуальным является поиск возможных упрощений моделей, позволяющих при этом производить качественные расчёты.

    Проблема: Классические методы моделирования взаимодействия молекул с внешним излучением приводят к «классическому» (непрерывному) спектру, тогда как из экспериментальных работ виден дискретный характер молекулярных спектров.

    Цель работы: Расчёт колебательных спектров двухатомных молекул.   

    Объект исследования: Молекулярная спектроскопия.

    Предмет исследования: Двухатомная молекула во внешнем поле.

     Задачи:

1) написать одномерную модель изменения молекулярного состояния;
2) составить компьютерную программу, позволяющую рассчитывать взаимодействие молекулы с внешним полем;
3) провести серию расчётов для выявления зависимости величины взаимодействия от частоты и интенсивности внешнего поля;
4) провести сравнительный анализ (полученных в этой работе) спектров с известными (рассчитанными или измеренными в других работах) молекулярными спектрами.

      Методы: 1) Численное дифференцирование (нахождение изменения волновых функций в пространстве);
2) Численное интегрирование (эволюция волновых функций во времени).
3) Метод Монте-Карло (случайный выбор начальных условий).

      Значимость работы:  Молекулярные спектры применяются в большом количестве приложений, где необходимо удалённое детектирование тех или иных молекул: от лабораторного и промышленного анализа газовых смесей до спектроскопического анализа космических объектов.

Литература

1. Бом Д. Квантовая теория. (2-е издание). М.: Наука, 1965
2. Фок В.А. Начала квантовой механики. М.: Наука, 1976
3. Фаронов В.В. Turbo Pascal 7.0. Начальный курс. Нолидж, 2000
4. Синай Я.Г. Курс теории вероятностей, изд. Московского университета, 1985

Задача Томсона для трех, четырех и шести зарядов 

Масленникова Елизавета Алексеевна

Муниципальное бюджетное общеобразовательное учреждение "Физико-математический лицей" г. Сергиев Посад.

Забавин Валерий Николаевич, доктор физико-математических наук

Краткая постановка цели и задач исследования:

     Доказать равновесность известных расположений на сфере трех, четырех и шести одинаковых зарядов  помощью методов элементарной математики.

Описание научно-исследовательской работы: 

     В начале XX века, конструируя модель атома, английский физик Джозеф Джон Томсон рассматривал задачу о равновесном расположении зарядов на сфере. После открытия атомного ядра эта задача была отложена, а в последнее время вновь привлекла к себе внимание математиков. В некоторых случаях равновесное расположение известно (для небольшого числа зарядов). В части этих случаев равновесность доказана. В работе [1] сообщается, что для трех и четырех зарядов доказательства выполнены с помощью неравенств между средним арифметическим, средним геометрическим и средним гармоническим, но самого доказательства не приводится. В этой же работе выполнены доказательства для шести и двенадцати зарядов с помощью методов, известных узкому кругу специалистов. 

Итоги исследования:

      Доказана равновесность известных расположений на сфере одинаковых зарядов для трех зарядов (правильный треугольник, плоскость которого проходит через центр сферы), четырех зарядов (правильный тетраэдр)и шести зарядов (правильный октаэдр).

Список литературы:

1. Н. Н. Андреев, В, А, Юдин. Экстремальные расположения точек на сфере// Математическое просвещение (третья серия). Вып. 1 - М,:МЦНМО, 1997.

2. В. А. Юдин. Минимум потенциальной энергии точечной системы зарядов//Дискретная математика. 1992. Т. 4. Вып.2. 

Решение проблемы навигации в крупных учреждениях с использованием концепции "Интернет вещей“

Автор: Джиджоев Владислав Муратович

Республика Северная Осетия-Алания, г. Владикавказ, МБОУ-лицей, 10 класс

Научный руководитель: Джаноян Елена Владимировна, учитель информатики, МБОУ-лицей г. Владикавказ

Цели и задачи: в данной работе рассматривается проблема навигации в распределённых учреждениях. Предлагается решение данной проблемы с использованием концепции «Интернет вещей», а в частности, технологии QR-кодов. Целью исследования являлась разработка информационной системы, решающей поставленную проблему, и её внедрение  на территории Северо-Кавказского горно-металлургического института.

Ход исследования: было проведено изучение проблемы навигации в крупных учреждениях и существующих способов её решения. Была предложена идея решения проблемы с использованием технологии QR-кодов. Был разработан и внедрён программный комплекс, решающий поставленную проблему.

Результат работы: разработанный программный комплекс состоит из двух частей – серверной и клиентской. Серверная часть является веб-приложением, состоит из базы данных, в которой хранится информация обо всех объектах данной организации. Клиентская часть – это приложения для мобильных операционных систем Android и iOS. В них встроен сканер QR-кодов, который способен распознавать коды, физически находящиеся на объектах, и отображать информацию об объекте на экране мобильного устройства.

Главным преимуществом разработанной системы является её гибкость и масштабируемость, которые заключаются в том, что систему можно использовать  в различных организациях организациях: в музеях, на заводах, в магазинах и т.д.

Весной 2015 года система интегрирована в СКГМИ. Созданы веб-сервер и мобильные приложения, необходимые для реализации проекта, развешены QR-коды на корпусах, постепенно они появляются и на этажах внутри зданий.

Ссылка на Android-версию: https://play.google.com/store/apps/details?id=com.expasys.skgmi

iOS версия находится на стадии публикации

Пример QR-кода для приложения:

Использованная литература:

1. Samuel Greengard. The Internet of Things, The MIT Press, 2015

ISBN: 978-02-62527-73-6         

2. Ovidiu Vermesan, Dr. Peter Friess. Internet of Things: converging technologies for smart environments and integrated ecosystems, River Publishers, 2013

ISBN: 978-87-92982-96-4

3. Дино Эспозито. Программирование с использованием Microsoft ASP.NET 4, издательство Питер, 2012

ISBN: 978-5-459-00346-8

4. Satya Komatineni. Dave MacLean. Pro Android 4, Apress, 2012

ISBN: 978-1-4302-3930-7

5. Matthew Knott. Beginning Xcode, Apress, 2014

ISBN: 978-1-4302-5743-1

Т.С.Гузеева,
МБОУ «Лицей №174"»

Научный руководитель: Хайбрахманова Н.В., учитель математики.

Оценка поведения квадратичной функции

Актуальность моей работы обусловлена тем, что задания на эту тему есть в ОГЭ, предстоящем мне в конце этого учебного года.

Предмет исследования: график квадратичной функции.

Объект исследования: функции и их графики.

Цель: Изучение изменения положения графика квадратичной функции с изменением дискриминанта и коэффициентов её формулы и применение графиков квадратичной функции в решении задач первой и второй частей ОГЭ по математике.

Исходя из цели, я поставила перед собой задачи:

• Рассмотреть некоторые функции.
• Провести анализ данных функций.
• Сделать выводы об оценке поведения функции у = ах² + bх + с и роли коэффициентов а, в и с.
• Рассмотреть различные варианты задания №23 из ОГЭ по математике.

Гипотеза: по дискриминанту и коэффициентам можно определить расположение графика квадратичной функции в координатной плоскости, не строя его.

Проектная значимость: Мы применили графики квадратичной функции в решении первой и второй частей ОГЭ по математике.

Методы исследования: сравнение, анализ, обобщение.

Заключение: Мы изучили изменение положения графика квадратичной функции с изменением дискриминанта и коэффициентов её формулы и применили графики квадратичной функции в решении задач первой и второй частей ОГЭ по математике. Наша гипотеза о том, что по дискриминанту и коэффициентам можно определить расположение графика квадратичной функции в координатной плоскости не строя его, подтвердилась.

Список использованной литературы:

1. Источник: http://interneturok.ru/ru/school/algebra/9-klass/chislovye-funktsii/svoystva-kvadratichnoy-funktsii-y-ax-sup-2-sup-bx-c
2. Источник: http://www.tofmal.ru/projects/graphics/kvadr.htm
3. Источник: http://raal100.narod.ru/index/0-277
4. Источник: http://repetitor-problem.net/kak-postroit-parabolu
5. Источник: http://or-gr2005.narod.ru/grafik/sod/ris20.html
6. Источник: http://www.mosrepetitor.ru/pages1/22/
7. Источник: http://egemaximum.ru/kvadratichnaya-funktsiya/

«Золотые пропорции красоты»

Работы выполнила: Романова Дарья Алексеевна, ученица 7 «А» класса муниципального  бюджетного образовательного учреждения  «Лицей», 13 лет,

Руководитель работы: Путанова Светлана Владимировна,  учитель математики  муниципального  бюджетного образовательного учреждения  «Лицей»

Основные тезисы работы:          

При изучении математики в 6 классе мы впервые встретились с понятием «Золотое сечение». Здесь из  исторической справки мы узнали, что золотым сечением или даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей.  Мне очень захотелось проверить: так ли это в действительности. Отсюда возникла тема моей исследовательской работы «Золотые пропорции красоты».

Объектом моего изучения будет золотое сечение.

Цель моего исследования:

выяснить проявляется ли правило золотого сечения в пропорциях человеческого тела.

Задачи:

1)  познакомиться с понятием «золотое сечение» и историей его возникновения;

2)  изучить методическую и научную литературу по теме исследования;

3) исследовать размеры тела человека и определить пропорции золотого сечения на примере своей семьи;

4) обобщить, систематизировать и закрепить полученные знания.

Я выдвинула следующие гипотезы:

1. Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
2. Золотое сечение можно найти и в пропорциях человеческого тела независимо от размера и возраста.

В процессе исследования я использовала следующие методы:

1. Общие методы: наблюдение, анализ, синтез;
2. Теоретический - от конкретных понятий к абстракции;
3. Эмпирические – измерение частей человеческого тела, сравнение, математические расчеты;

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

            Согласно Пифагору гармония имеет численное выражение, то есть, она связана с концепцией числа. Евклид излагает теорию Платоновых тел, которая является существенным разделом геометрической теории Золотого Сечения. Платон рассказывал, что Вселенная устроена согласно «золотому сечению». Аристотель нашел соответствие «золотого сечения» этическому закону.

            Части красиво сложенного человеческого тела находятся в определенной пропорции, знает каждый: недаром мы говорим о пропорционально сложенной фигуре.  Деление тела точкой пупа – один из основных показателей золотого сечения.

            Лицо считается пропорциональным, если его можно разделить условно линиями по горизонтали на 4 равные части: от верхушки головы до края волосяного покрова, затем выделяется область лба, а следующая линия проводится прямо под носом.

            Достаточно лишь приблизить ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг. Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца).

В своей исследовательской работе я поставила перед собой задачу  - определить пропорции золотого сечения на примере моей семьи.

            В нашей семье четыре человека: папа, мама, я и мой брат Глеб. Все мы разных размеров и возрастов – папе 39 лет, маме 35 лет, мне 13 лет, Глебу 5 месяцев. Таким образом, в процессе исследования я могла точно выяснить, проявляется ли правило золотого сечения в фигурах мужчин и женщин, а также зависимость его от пола и возраста.

            Наши расчеты показывали, что у папы, мы и меня размеры тела очень близки к значению  золотого сечения 1,618, только показатели Глеба очень далеки от золотого сечения, они колеблются от 1, 9 до 1, но это и не удивительно, ведь он еще совсем малыш. Так как пропорции наших тел, очень близки к золотому сечению, можно сделать вывод, что при нашем росте и возрасте, мы действительно имеем хорошую фигуру.

            При исследовании размеров лица и рук выявились, что некоторые пропорции лица и рук действительно близки к значению золотого сечения, а некоторые вовсе и нет. Так расстояния от кончика подбородка до макушки  и от кончика подбородка до верхней линии бровей, а также  от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки подчинены правилу золотого сечения у нас троих за исключением Глеба. А вот параметры от кончика подбородка до ноздрей  и от кончика подбородка до кончика верхней губы,  от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей у всех членов нашей семьи далеки от значения золотой пропорции и колеблются от 1,25 до 4.

            Есть несоответствия и в параметрах наших рук. Так при сравнении соотношения длины среднего пальца и суммы двух первых фаланг пальца у всех членов нашей семьи наблюдается число близкое к золотому сечению. А при сравнении длины среднего пальца с длиной мизинца только у меня и у Глеба это соотношения составляют значение 1,6, что близко к золотому сечению.

            По результатам исследования можно сделать следующие выводы:

            Золотое сечение в пропорциях тела членов нашей семьи в основном соблюдается, за исключение Глеба. Папины значения колеблются от 1,6 до 1,630; мамины значения от 1,6  до 1,666;  мои значения  от 1,611 до 1,636. Таким образом, папины размеры тела наиболее близки к золотому сечению, следовательно, его фигура более близка к совершенству с точки зрения математических расчетов. Размеры частей тела  Глеба колеблются от 1,065 до 1,939. Это нас не удивляет, так как ему всего 5 месяцев. Наши расчеты подтвердили исследования профессора Цейзинга, что значения размеров частей человеческих тел находятся в золотой пропорции независимо от пола, но зависят от возраста человека.

            Также наше исследование показало, что некоторые размеры частей наших лиц близки к значению золотого сечения, а некоторые далеки от него. Тоже касается и показателей наших рук. Так у меня и Глеба размеры пальцев очень близки к значению золотой пропорции, а вот у мамы и папы не всегда.

            Таким образом, можно сделать вывод: золотое сечение в пропорциях человеческого тела в основном соблюдается. Причём, с взрослением  ребёнка эти пропорции становятся более совершенными с точки зрения математики и общепризнанных классических  законов красоты. 

            В данной работе я раскрыла  тайны “золотого сечения”. Узнала, что существует такая золотая точка на любом отрезке, которая обеспечивает, присутствие красоты, соразмерности частей человеческого тела. Проделала  практическую работу на нахождение “золотого сечения” в размерах частей тела, лица и рук членов своей семьи. Я считаю, что в результате проделанной работы я достигла поставленных перед собой целей и задач, а также при помощи используемых методов частично нашла подтверждение выдвинутых мной гипотез.

            Таким образом, можно сделать вывод, что золотое сечение вовсе не математический вымысел. Это на самом деле продукт закона природы, основанный на правилах пропорциональности.

            На примере моей работы вы можете очень легко и быстро проверить: «А является ли ваша фигура совершенством?» Только не расстраивайтесь, если окажется, что вы далеки  от Аполлона, Венеры Милосской и Мадонны Леонардо да Винчи, наверное, не в этом счастье. Вспомните поговорку: «Красивым быть - не значит им родиться, ведь красоте мы можем научиться».

Список использованной литературы и

информационных источников

1. Атанасян Л.С. и др.  Геометрия. 7 - 9 классы.   10-е изд. - М.: Просвещение, 2010. - 384 с.
2. Азевич А.И. Двадцать уроков гармонии: гуманитарно-математический курс / А.И. Азевич. – Москва: Школа-Пресс, 1998. – 160 с.
3. Васютинский Н. “Золотая пропорция” – М., ”Молодая гвардия”, 1990. -238с.
4. Виленкин Н. Я. Математика. 6 класс: учеб.  для общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. - 32-е изд., стер. — М.: Мнемозина, 2014. — 288 с.: ил.
5. Гарднер М. Математические головоломки и развлечения: 2-е изд., испр. и дополн. /Пер. с англ. — М.: «Мир», 1999, 447с, ил.— (Математическая мозаика)
6. Стахов А. Коды золотой пропорции. - Москва: Радио и связь. Редакция литературы по кибернетике и вычислительной технике, 1984. - 152 с.
7. Пидоу Д. Геометрия и искусство. – М.: Мир, 1989. 3. Журнал «Квант», 1973, № 8. 4. Журнал «Математика в школе», 1994, № 2; № 3.
8. Математика. Еженедельное учебно-методическое приложение к газете «Первое сентября» №42, 2000, 32 с.
9. http://kvant.mccme.ru/1973/08/zolotoe_sechenie.htm
10. http://www.ed.vseved.ru/

Автор работы: Курлыков Игорь Алексеевич, ученик 11А класса МАОУ СОШ с.БЕРДЮЖЬЕ. Руководитель:Петрулёв Пётр Николаевич

Цель : Создание плана-проекта разработки. Разработка программной (теория) и технической части. Тестирование и моделирование ситуаций и возможностей   использования.  Анализ итогов . Сравнение с моделями сторонних производителей, в данной сфере. 

Актуальность:

Проект беспилотный комплекс «Яга»  - новый взгляд и доработка, совершенствование и нововведения  в сфере программных комплексов и беспилотных летательных аппаратов.

В том числе это попытка изучить все свойства устройств ,программы и алгоритмы полёта . физику .А также изучить сферу.Данное проектное исследование  предлагает не только создание  единой базы обработки и классификации полученных данных , но и создание источника информации исследовательского направления на базе комплекса . На сегодняшний день этот комплекс является единственным в своём роде.  

Идея: создать коцепт системы предварительно изучив все что нужно , в регультате получив готовый продукт 

Методы исследования:

Способы начального исследования для получения конкретной стартовой информации для дальнейшей обработки:

1. Исследование и сравнение уже существующих беспилотных аппаратов.
2. Выявление минусов и плюсов, как программных так и технических.
3. Предположение о потребительском спросе на комплекс.
4. Расчёт ценовой характеристики.
5. Практическая нужда, в комплексах такого рода.
6. .Возможность создания производства в  масштабах страны или области для решения конкретных задач

Основные задачи которые может решить комплекс

1.Беспилотный контроль местности

2.Аэросьёмка

3.Измерение погодных условий

4.Исследование каких либо территорий и агроклиматических ресурсов

6.Работа  условиях городской среды

7.Работа в условиях низкой температуры(-30с)

8.Режим спасения . Усиление сигнала GPRS.

9.Анализ загрезнённости окружающей среды

10. Работа на месторождениях нефти и газа . А также анализ состояния труб газо – нефтепроводов.

11.Экстренное реагировани

12. Работа в системе из нескольких аппаратов

13.Дополнительные программируемые функции

Особенности ориентации комплекса является то , что  он может выполнять задачи в автоматическом режиме при этом сам выбирает путь следования.

Разработка Полётного Контроллера  CopterBrain 2  .

CopterBrain – этом плата для управления полётом , включающая всё , что нужно полётному контроллеру

Новизна

1.Объеденение исследовательского комплекса и беспилотного аппарата

2.Объединение информационной системы и комплекса

3.Уменьшение цены

4.Нововведения в конструкции беспилотных аппаратов

5.Собственное программное обеспечение

6.Автоматизация

7.Полётный контроллер CopterBrain

Итоги

Создан  программный комплекс

Проведена частичная модуляция задач (пака  TEST)

Создан первый прототип

Создан план и способы его реализации

Созданы новые устройства

Создано новое ПО

Протестирована работа прототипа в связке с системой

Список использованной литературы  

1. http://habrahabr.ru/post/227425/
2. http://www.youtube.com/user/0arduinoLab
3. http://www.youtube.com/user/AmperkaRu
4. http://www.youtube.com/user/MacPuffdog
5. http://www.youtube.com/user/tolik7772
6. http://www.youtube.com/channel/UCTXOorupCLqqQifs2jbz7rQ
7. http://arduino.ru/forum/proekty/tyazhelyi-kvadrokopter-na-arduino-mega-2560
8. http://geektimes.ru/post/256822/
9. http://cppstudio.com
10. https://ru.wikipedia.org/wiki/C%2B%2B
11. https://ru.wikipedia.org/wiki/%D0%9A%D1%80%D1%8B%D0%BB%D0%BE_%D1%81%D0%B0%D0%BC%D0%BE%D0%BB%D1%91%D1%82%D0%B0

КОМБИНАТОРНАЯ ГЕОМЕТРИЯ

Автор: Ницер Ксения Александровна

г. Кемерово, МБНОУ «Городской Классический Лицей»

Руководитель: Борздун Ольга Владимировна, учитель математики МБНОУ «ГКЛ»

Комбинаторная геометрия - раздел, родственный дискретной геометрии и находящийся на стыке элементарной геометрии и теории выпуклых тел.

Актуальность нашей работы заключается в том, что в настоящее время популярность комбинаторной геометрии набирает обороты, и мы можем встретить ее применение в самых различных отраслях. Также в последнее время в олимпиадах часто используются задачи на теоремы комбинаторной геометрии.

Цель работы: изучение основ комбинаторной геометрии, подробное изучение некоторых ее теорем и решение задач по этой теме.

Объект исследования: комбинаторная геометрия

Предмет исследования: теоремы комбинаторной геометрии и решение задач на эти теоремы.

В работе подробно рассмотрены и изучены Теорема Хелли и Задача Борсука, а также предложены как часто встречаемые задачи по этим теоремам, так и задачи самостоятельного решения.

Задачи:

• Изучить историю развития предмета нашего исследования, используя литературные источники, включая электронный ресурс;
• Изучить основные теоремы комбинаторной геометрии;
• Решить ряд задач с использованием изученных теорем.

Гипотеза: научно-обоснованное использование классических теорем комбинаторной геометрии в практике будет результативным, если:

• Изучены теоретические аспекты проблемы;
• Проведена систематизация имеющейся информации;
• Поставлена и решена адекватная практическая задача.

В ходе данной работы были рассмотрены основные теоремы комбинаторной геометрии, такие как Теорема Хелли и Задача Борсука. Также была изучена история развития предмета данного исследования, и решены задачи с использованием рассмотренных теорем.

Список использованной литературы:

1. Райгородский А. М. Проблема Борсука. – М.: МЦНМО, 2006. — 56 с.
2. Прасолов В. В. Задачи по планиметрии. Часть 2, издание третье, стереотипное. Издательская фирма "Физико-математическая литература" РАН 117071, Москва
3. Башмаков М. И. Математика в кармане «Кенгуру». Международные олимпиалы школьников. – М: Дрофа, 2010. – 297 с.
4. Протасов В. Теорема Хелли и вокруг нее (статья).
5. wikipedia.org

Исследовательский проект: «Применение Пифагоровых троек для решения геометрических задач»

Николаева Надежда Геннадьевна

Муниципальное автономное образовательное учреждение лицей № 37 г.Челябинск

Научный руководитель: Савченко Ольга Викторовна, учитель математики высшей категории МАОУ лицей № 37 г.Челябинска

Цели и задачи: Собрать сведения о пифагоровых тройках и их применение для решения практических задач курса геометрии и задач ЕГЭ типа В4. Показать уникальность открытия Пифагора и дать определение понятия пифагоровых троек. Описать простые способы формирования пифагоровых троек. Проанализировать возможности применения теоремы Пифагора, применения полученных знаний о пифагоровых тройках для их практического применения при решении задач.

Актуальность и новизна исследования: Проблема, о которой пойдёт речь в моей работе выглядит довольно простой потому, что в основе её лежит математическое утверждение,  известно каждому - теорема Пифагора. Пифагоровы тройки известны очень давно. В данной  работе мы рассмотрим, как  применить их при решении геометрических задач ОГЭ и ЕГЭ.  Сейчас пифагоровы тройки изучаются в контексте теоремы Пифагора и являются ее целочисленными решениями, но мы хотим доказать, что пифагоровы тройки нужно изучать как самостоятельную тему в математики, т.к. она помогает при решении геометрических задач.

Описание научно-исследовательской работы: В ходе работы мы  1.Изучили литературные источники.2.Изучили свойства пифагоровых троек и способы формирования триад  3.Проанализировали применение пифагоровых троек и на основе этого провели исследования на учащихся 8-х классов

Исследование проводили на учениках 8-х классов. Сперва предлагали решать задачи простым способом, а затем, рассказав им про пифагоровы тройки решить задачи с их применением. Все данные подвергались статистической обработке. Из проведенного исследования  видно, что время, затраченное на решение задач, с применением пифагоровых троек уменьшилось, а процент правильных решений увеличился. Это позволяет сделать заключение о положительном применении свойств Пифагоровых троек для решения геометрических задач.

Итоги исследования: Применение пифагоровых троек в решении задач позволяет экономить время, избегать вычислительных ошибок. Знание этих троек подталкивает к иному решению задачи. Проведенные исследования показывают эффективность применения пифагоровых троек при решении геометрических задач. В целях экономии времени и избежание вычислительных ошибок рекомендуем объяснять на уроках способы формирования пифагоровых троек и стремиться к их применению на практике.

Список использованной литературы:

1. Аносов Д.В. Взгляд на математику и нечто из нее. - М.: МЦНМО, – 2003.
2. Вольфсон Г.И. и др. ЕГЭ 2013. Математика. Задача С6. – М: МЦНМО, 2013.
3. Гельфонд А.О. Решение уравнений в целых числах. – М.: Гос.изд.техн.-теор.литературы,1957.
4. Горбачев Н.В. Сборник олимпиадных задач по математике. – М.: МЦНМО,2004.
5. Колосов В.А. Теоремы и задачи алгебры. Теории чисел и комбинаторики. – М.: Гелиос АРВ, 2001.
6. Кордемский Б.А, Математическая смекалка. – М.: Наука, 1991.
7. Оре О. Приглашение в теорию чисел  - .М.: Наука, 1980.
8. Радемахер Г., Теплиц О. Числа и фигуры. – М.: Наука 1966.
9. Степанова Л.Л. Избранные главы элементарной теории чисел. – М.: Прометей, 2001.
10. Шклярский Д.О. и др. Избранные задачи и теоремы элементарной математики. Часть 1. Арифметика и алгебра. – М – Л.: Гос.изд.техн.-теор.литературы,1950.
11. Банк заданий (адрес сайта htt://mathege.ru/or/ege/).

Тезисы научно-исследовательской работы

1. Название научно-исследовательской работы: «Педальный треугольник»
2. ФИО автора работы: Аржиманова Анна Шакировна
3. Образовательное учреждение, в котором обучается автор работы: Гимназия-комплекс №26 с углубленным изучением французского языка
4. ФИО, должность и место работы научного руководителя: Мавлянова Юлдуз Ашуровна – учитель математики гимназии - комплекс №26 с углубленным изучением французского языка
5. Краткая постановка цели и задач исследования:

Цель: Рассмотреть теоретические аспекты педального треугольника, точки Брокара и их практическое применение.

Задачи:

• Дать общую характеристику треугольнику как геометрической фигуры.
• Рассмотреть педальный треугольник как разновидность треугольника.
• Познакомиться с точкой Брокара и прямой Симпсона.
• Рассмотреть свойства педального треугольника и доказать некоторые из них.
• Показать практическое применение свойств педального треугольника и точки Брокара при решении геометрических задач повышенной трудности.

6.Основной текст тезисов.

Для решения геометрических задач часто используется метод вспомогательных фигур, который упрощает и помогает решить задания, которые, казалось бы, невозможно решить. Одним из самых удобных является метод использования вспомогательного треугольника.

Тем не менее, изучаемые конструкции, связанные с треугольником, далеко не исчерпывают всех возможных. Примером тому служит педальный треугольник.

Пусть Р – любая точка внутри данного треугольника АВС, и пусть перпендикуляры, опущенные из точки Р на стороны ВС, СА, АВ треугольника, будут РА₁, РВ₁ и РС₁. треугольник А₁В₁С₁, вершинами которого являются основания этих перпендикуляров, называется педальным треугольником треугольника АВС для «педальной точки» Р.

Если при построении педального треугольника углы получаются равными, то они называются углами Брокара, а педальная точка - точкой Брокара.

В научно-исследовательской работе рассматриваются теоремы и свойства педального треугольника и их применение при упрощении решения заданий высокой сложности.

7.Актуальность исследования обусловлена ежегодным усложнением заданий ОРТ, ЕГЭ, вступительных тестов вузов, что требует углубленных знаний не только в алгебре, но и геометрии.

8.Значимость и новизна исследования: Если выяснить свойства педального треугольника, месторасположение точки Брокара и овладеть ими, мы получим объективную возможность для решения задач повышенной сложности.

9.Итоги исследования: В данной работе мы рассмотрели понятия и свойства педального треугольника, прямой Симсона, точки и углов Брокара, а на наглядном уровне месторасположение точки Брокара, исследовали свойства педального треугольника. Мы убедились, что знание свойств педального треугольника, месторасположения точки Брокара значительно упрощают решение сложных математических задач. И если выяснить свойства педального треугольника, месторасположение точки Брокара и овладеть ими, мы действительно получаем объективную возможность для решения задач повышенной сложности.

Приложение к основному тексту тезисов работы:

10. Список использованной литературы:

1. Коксетер Г.С., Грейтцер С.Л., Новые встречи с геометрией. – М: Наука, 1978;
2. Кубышева М.А., Избранные вопросы геометрии.- М, 2006;
3. Прасолов В.В., Задачи по планиметрии. – М: МЦНМО, 2006;
4. Прасолов В.В., Точки Брокара. Ж: Квант № 1, 1992, с.42;
5. Фетисов А.И., Геометрия в задачах. – М: Просвещение, 1977;
6. Журнал «Математика в школе», №5, 1999 г.
7. Шарыгин И.Ф., Геометрия 7-9 класс. – М: Дрофа, 2006;
8. Учебно-тренировочные материалы для подготовки ЕГЭ 2007-2009

                                 Центральные точки треугольника,

                            связанные с некоторыми экстремумами

                                  Тимофеев Даниил

                МБОУ ''Физико-математический лицей ''г. Сергиев Посад,

                     Научный руководитель: Забавин Валерий Николаевич

               Цель работы: узнать, являются ли центральными точками треугольника центр вписанного в него равностороннего треугольника минимальной площади и центр вневписанного равностороннего треугольника минимальной  площади (цель работы подсказана наблюдением, что большинство замечательных в интуитивном смысле точек треугольника являются центральными [1]).

                Точка называется центральной, если её барицентрические координаты как функции длин сторон обладают свойствами цикличности, симметрии по двум аргументам и однородностью [1].

                  Показано, что эти точки имеют барицентрические координаты (выраженные через длины сторон и радиус  описанной окружности)

                          p:q:r=a*(√3*a*R+b*c):b*(√3*b*R+a*c):c*(√3*c*R+b*a).

                          p:q:r=a*(-√3*a*R+b*c):b*(-√3*b*R+a*c):c*(-√3*c*R+b*a).

       Уравнение прямой, проходящей через эти точки, в барицентрических координатах:

p·(a²-b²)+q·(c²-a²)+r·(b²-c²)=0,также на данной прямой лежат точка Лемуана и точка пересечения медиан.

            Вывод: полученные координаты удовлетворяет условиям, сформулированным выше, значит, найденные точки – центральные. Эти две точки отсутствуют в энциклопедии профессора Кимберлинга[2].

                                                        Используемая литература              

1. А. Г. Мякишев. Элементы геометрии треугольника. Библиотека “Математическое просвещение”Bып.19.-M.:МЦНМО,2002.
2. http://faculty.evansville.edu/ck6/encyclopedia/ETC.html

В даннойработе рассказывается о математическом методе определения загрезнения окружающей среды с помощью листье деревьев

Слаушевская Евгения Александровна

Муниципальное автономное общеобразовательное учреждение  гимназия №10 им. А. Е. Бочкина г. Дивногорск

Научный руководитель - М. Е Слаушевская, учитель информатики, МАОУ гимназия №10 им. А. Е. Бочкина, г. Дивногорск

Цель: Исследование возможности коллективного решения интеллектуальной задачи по нахождению местоположения цели.

Задачи:

1. Составить программу, моделирующую поведение роя при решении поставленной задачи.
2. Исследовать построенную модель.

На сегодняшний день мы достигли того этапа в развитии техники, когда нам приходится иметь дело с системами состоящими из огромного количества динамически изменяющихся, взаимосвязанных и однородных сущностей. Для управления ими традиционные централизованные методы уже не годятся. Поэтому интеллект роя — единственный способ продолжать развитие. Интеллект роя – это метод оптимизации, описывающий коллективное поведение децентрализованной самоорганизующейся системы.

Раздел программирования мультиагентных систем, а именно исследования, связанные с интеллектом роя, на сегодняшнем этапе изучен недостаточно. Основоположниками изучения данного вопроса являются Херардо Бени и Ван Цзин. Термин «Интеллект роя» был введен ими в 1989 году. Современными авторами постоянно предлагаются новые варианты развития алгоритма роя частиц для улучшения производительности данного метода. Существует несколько тенденций в этих исследованиях, одна из которых предлагает создать гибридный оптимизационный метод. Другая тенденция предлагает каким-либо образом ускорить работу метода. В соответствии с поставленными мировым ученым сообществом  целями, своё теоретическое исследование я посвящаю  вопросу изучения классического алгоритма роя.

Объект исследования: мультиагентная интеллектуальная система «рой».

Предмет исследования: поведение системы при нахождении цели.

Методы исследования: математическое моделирование.

Задачей моделируемых объектов, условно названных «птицами», является нахождение цели, условно названной «пища».

Для правдоподобного отображения движения птиц взяты несколько формул, описанные в работе Кеннеди и Эберхарта в 1995 году:

а)  v_i=v_i+a₁*rnd()*(pbest_i-x_i)+a₂*rnd()*(gbest_i-x_i),

где v– вектор скорости частицы (v_i– его i-ая компонента), a₁, a₂ -  постоянные ускорения, pbest– лучшая найденная частицей точка, gbest– лучшая точка из пройденных всеми частицами системы, x– текущее положение частицы, а функция rnd() возвращает случайное число от 0 до 1 включительно. По данной формуле вычисляется скорость каждой частицы роя, исходя из ее лучшего положения, лучшего положения роя.

б)  x = x +v

По этой формуле вычисляется положение частицы после расчета ее скорости.

в)  d=((x₂-x₁)²+(y₂-y₁)²)^1/2

По этой формуле вычисляется расстояние между двумя точками на плоскости. Она используется при вычислении: расстояния до цели для каждой точки, pbest, gbest.

Программная реализация модели интеллекта роя выполнена в среде Delphi 7.

Чтобы проанализировать полученную модель, мною было проведено несколько тестов. В каждом из них было проведено по 5 проверок для каждого случая и после этого посчитано среднее время нахождения цели. Время рассчитывалось с помощью количества итерации, которое появляется в правом нижнем углу после нахождения цели(1 итерация = 0,1 сек).

В первом тесте я изменяла количество «птиц». Было рассмотрено 5 случаев: для 10, 50, 100, 150, 200 «птиц». Ускорение а₁=0,1, а₂=0,1. Цель постоянно располагалась в центре поля. Тест показал, что при увеличении количества объектов время схождения алгоритма уменьшается, но при очень большом количестве «птиц» разница достигает всего нескольких сотых секунды.

Во втором тесте я изменяла ускорения: а₁ – ускорение для отдельной частицы и  а₂ – ускорение для всего роя. Данный тест выявил:

• На движение роя в большей степени влияет ускорение самого роя.
• При увеличении ускорения сходимость алгоритма повышается.
• При уменьшении ускорения всего роя, частицы начинают двигаться, почти не обращая внимания на перемещение других частиц роя.
• При отсутствии ускорения роя, частицы не могут найти цель.

В ходе компьютерного эксперимента, который позволил продемонстрировать поведение «интеллекта роя» по нахождению объектом цели, мне удалось показать, как работает мультиагентная система и выявить некоторые закономерности. Исследование модели выявило, что действуя совместно, объекты могут найти цель гораздо быстрее, чем поодиночке: при увеличении количества объектов роя время нахождения цели уменьшается.

Данное исследование важно в исследовании построения искусственного интеллекта и интеллекта роя в частности. Исследование мультиагентных систем планируется продолжить на примере других, уже более сложных задач, например, в робототехнике с использованием платформы Arduino.

Библиографический список

1. Swarm Intelligence by James Kennedy and Russell C. Eberhart
2. PSO Tutorial, Xiaohui Hu, 2006 - http://www.swarmintelligence.org/tutorials.pdf
3. The Particle Swarm Optimization Algorithm Jaco F. Schutte EGM 6365 - Structural Optimization Fall 200
4. Лебедев Олег Борисович, Журнал Известия Южного федерального университета. Технические науки, Выпуск № 7 / том 120 / 2011 -http://cyberleninka.ru/article/n/obzor-evolyutsionnyh-metodov-optimizatsii-na-osnove-roevogo-intellekta
5. Миллер Питер. Роевой интеллект, 2007. - National Geographic Россия - http://www.national-geographic.ru/ngm/200708/article_139/

К.Ю.Станкевич,
МАОУ «Академический лицей»

Научный руководитель: Литвин А.В., заведующий лабораторией информатики в Академическом лицее г. Магнитогорска, учитель информатики высшей категории

Разработка кроссплатформенного шутера “DEAD SURVIVAL” посредством UNITY 3D

Актуальность: Создание игр — это не только средство заработка, но и хобби. В  последнее время написание видеоигр стало приятным делом. Различные языки программирования способствуют увлекательному кодингу, а разнообразные движки делают этот процесс  интуитивно понятным. Создание игр — это одна из основ развития современных IT-технологий.

Проблема: Высокая цена и необходимость интернет-подключения вынуждают людей отказываться от психологической и эмоциональной разгрузки за игрой.

Предмет: Предметом данного проекта является создание игры в среде разработки Unity 3D 5 и Visual Studio 2012.

Объект: Шутер от первого лица под названием "Dead Survival".

Цель: Основной целью моей работы является  создание игры, которая будет пользоваться популярностью.

Для достижения цели мной были изучены среды разработки Unity 3D 5, 3DMax и Visual Studio 2012, языки программирования C# и JavaScript.

Задачи:

1. Исследовать основные понятия игры от первого лица.
2. Изучить среду разработки Unity 3D 5 и Visual Studio 2012.
3. Создать кроссплатформеную игру «Dead Survival».
4. Оценить популярность продукта.

Проектная значимость: Нами была разработана игра шутер от первого лица, которая позволяет отвлечься от дел, расслабиться, снять психологическую и эмоциональную нагрузку.

Метод исследования: анализ литературы, поиск аналогов, проектный метод, обобщение полученных знаний.

Заключение: В результате нашей работы были обозначены следующие термины: подпрограмма, Unity 3D 5, Visual Studio 2012, C#, 3DMax. Сделан вывод, что выше упомянутые среды разработки являются современными, перспективными и популярными. Была создана кроссплатформенная игра – шутер от первого лица «Dead Survival», которая пользуется относительной популярностью среди игроков, как в операционной системе Windows так и на Android и IOS.

Список литературы:

1. Люгер Дж. Ф. Искусственный интеллект - 4изд - 2003
2. Мультиплатформенная разработка на C#. Джозеф Хокинг
3. Переход к MicrosoftVisualStudio 2012 ПатрисПелланд, Паскаль Паре, Кен Хайнс
4. Эндрю Троелсен Язык программирования C# 5.0 и платформа .NET
5. Team foundation server planning guide. Практическое занятие. Джим Шубрит, ПрасаннаРамкумар, Тина Эрви, Вилли-Петер Шауб.
6. Unity Game Development Essentials [2009, Will Goldstone].
7. Game Development for iOS with Unity3D 2012 Jeff W. Murray

Актуальность: Какие возможности на практике открывает нанотехнология, и насколько кардинально нанотехника изменит нашу жизнь?

Цели:

1. Почему же именно наноразмеры привлекли внимание ученых?
2. Познакомиться с основными достижениями и проводимой исследовательской работой в области нанотехнологий в мире.
3. Как развивается Российская наука в области нанотехнологии?
4. Какие опасности несут с собой нанотехнологии?

Задачи:

1. Узнать основные открытия в области нанотехнологий и выявление основных проблем связанных с их применением в повседневной жизни;
2. Научиться анализировать, сопоставлять факты, выделять главное, устанавливать причинно - следственные связи, работать с различными литературными источниками;
3. Понять актуальность практического применения полученных знаний в повседневной жизни.

«Ах, это неизведанное время…»

Дзейн Диана Юрьевна

учащаяся 5 «Д» класса ГУО «Средняя школа № 21г. Могилева»

 Научный руководитель: Глазко Екатерина Николаевна, учитель математики ГУО «Средняя школа № 21 г. Могилева»

Объект исследования: календари.

Цель исследования: Исследовать соответствие используемого календаря с астрономическим.

Гипотеза исследования: календари, используемые сейчас, не соответствуют временам года.

Задачи:

1. Познакомиться различными календарями;
2. Просчитать, когда будет Пасха в ближайшие 20 лет;
3.  Просчитать отставание используемого календаря от астрономического   за период с 1918 по 2013годы;
4. Выяснить, когда зима наступит летом.

Итоги исследования:

1. Составлена таблица дат Пасхи на ближайшие 20 лет, проведен расчет соответствия природного календаря и того, что мы пользуемся. 
2. Нашла и ответ на вопрос: «Когда зима наступит летом?». Это произойдет через 18 веков.

Список используемых источников

1. http://www.wikipedia.org/ - Википедия (свободная энциклопедия).
2. Время, системы измерения // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
3. Идельсон Н.И. История календаря, 1976.
4. Климишин И.А. “Заметки о нашем календаре”,1967.
5. Красильников Ю.Д. “Солнце, луна, древние праздники и новомодные теории”, 1999.
6. Малявин Дмитрий. «Вечные» карманные календари СССР.

 Варич Илья Александрович, Плотников Александр Ярославович, 11 класс

МБОУ «СОШ № 31», МБНОУ «Городской классический лицей»

Научный руководитель: Глухова Ольга Юрьевна, канд. пед. наук, зав. кафедрой фундаментальной математики ФГБОУ ВПО «КемГУ»

            Для построения теории оригами используется система аксиом. Аксиомы оригаметрии предложил живущий в Италии японский математик Хумиани Хузита. Таких аксиом, с его точки зрения, всего шесть. В 2002 году японский оригамист Коширо Хатори обнаружил сгиб, который не описан в аксиомах Х. Хузита.

Цель исследования: рассмотреть геометрию с помощью оригаметрических методов.

Задачи:

1. Познакомиться с аксиоматикой оригаметрии.
2. Установить связь оригаметрии и геометрии Евклида.
3. Решить геометрические задачи оригаметрическими методами.

В работе на основе семи аксиом в теоретической части предложено доказательство теоремы о том, что сумма углов треугольника равна 180º.

Также, в теоретической части работы разобраны решения двух планиметрических задач.

            В практической части представлены разработки экспериментов со складыванием бумаги. Даны решения планиметрических теорем, выполненных самостоятельно с использованием оригами (тексты теорем приведены в публикации Т. Дрогаченко без решения):

            Теорема 3. Соответственные углы, образованные при пересечении двух параллельных прямых секущей, равны.

            Теорема 4. Сумма внутренних односторонних углов, образованных при пересечении двух параллельных прямых секущей, равна 180º.

            Решены самостоятельно две задачи:

1. На сторонах угла О отмечены точки А и В так, что ОА=ОВ. Через эти точки проведены прямые, перпендикулярные к сторонам угла и пересекающиеся в точке С. Докажите, что луч ОС – биссектриса угла О.
2. Прямая, перпендикулярная к биссектрисе угла А, пересекает стороны угла в точках М и N. Докажите, что треугольник АМN – равнобедренный.

В ходе выполнения научно-исследовательской работы самостоятельно сконструированы три модели оригами.

Научно-исследовательская работа 

на тему:  

«Создание аркады на движке Unity»

Выполнил: Константинов Михаил Борисович 7 класс, РЦДТТ, МБОУ-лицей 

Северная Осетия Алания, г.Владикавказ

Руководитель: Константиниди В. В., преподаватель МБОУ-лицей, РЦДТТ

Основная идея исследования:

В данной исследовательской работе рассматривается создание аркадной игры на движке Unity.

Актуальность темы исследования подтверждается неослабевающим интересом к аркадным играм, которые развивают ловкость и помогают расслабиться после тяжёлого трудового дня.

Основные цели исследования:

• Изучить движок Unity
• Разработать свой мир 
• Освоить начала C#
• Изучить Физику в Unity

По сюжету игры персонаж Furry на пути к финишу путешествует по дому, преодолевая препятствия, затем попадает в лабиринт.

Для обработки физического поведения героя использован движок Unity Rigidbody2D. Он управляется из скрипта,задающего максимальную скорость и силу прыжка.

Использованы скрипты,управляющие камерами и пользовательским меню.

Проведённая работа позволила мне изучить движок Unity, освоить начала C#, разработать свой игровой мир.

 Список используемых Интернет-ресурсов: 

1. https://ru.wikipedia.org/wiki/Аркада_(игра) 

1. https://ru.wikipedia.org/wiki/C_Sharp 

1. http://unity3d.com/ru/

Методы решения системы линейных алгебраических уравнений.

Миронов Михаил Сергеевич, ученик 11 класса

МОУ СОШ №8 г.Каменки.

Руководитель: Буркина Ирина Николаевна,учитель математики МОУ СОШ №8 г. Каменки.

Цель работы: подготовить материал для методического пособия для школьников старших классов на тему: «методы решения систем линейных алгебраических уравнений» опираясь на материал не изучаемый в школьной программе.

Задачи:

• Изучить методы решения систем линейных алгебраических уравнений не изучаемые в школьной программе.

• Научиться решать системы линейных алгебраических уравнений.

Описание научно-исследовательской работы: работа состоит в рассмотрении основных методов решения систем линейных алгебраических уравнений не изучаемых в школьное программе :

• метод Гаусса (метод заключается в последовательном исключении неизвестных)

• метод Крамера (нахождение отношения орпделителей матриц из коэффициентов перед переменнымси и свободными членами)

• метод братной матрицы(решение матричного уравнения)

• Метод простой итерации или метод Якоби

• Метод Гаусса – Зейделя

• Решение нормальной системы уравнений из 2 уравнений методом умножения и деления.
  Актуальность и значимость работы: знание методов решения систем уравнений и возможность их упрощать помогает решать поставленные перед человеком задачи более эффективно и быстро. И чем раньше человек сможет изучить эти методы и попрактиковаться в их применении, тем ему будет проще в дальнейшем работать с САУ. Именно такие цели я преследую при создании методического пособия.

Данная работа являетмся продолжение уже проделанного исследования и вместе с ним послужит для создания матодоческого посибия.

Итоги исследования: я считаю, что данная тема актуальна не только для меня, но и для учащихся различный образовательный учреждений. Думаю, что поставленные перед собой цели и задачи я выполнил: изучил методы решения СЛАУ, научился применять их на практике. Так же достаточно углубленно исследовал применение систем уравнений.

Считаю, что представленный материал вместе с уже проделанной до этого работой может послужить для составления методического пособия по математике на данную тему. Что должно упростить изучение математики ученикам образовательных учреждений.

Список литературы и интернет ресурсов:

1. wikipedia.org.ru

2. «Методическое пособие по математике для учащихся старших классов и абитурентов»И.М.Шабунин, Ю.В.Сидоров, доценты Н.Х.Агаханов, М.В.Балашов, И.И.Богданов, С.Е.Городецкий, П.А.Кожевников, С.П.Коновалов. М Физматкнига 2015г.

3. «Высшая математика в упражнениях и задачах» П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова М. ООО»Издательский дом «ОНИКС 21 век» 2003г.

4. Баврин И.И. (раздел математика). Большой справочника школьника. М.Дрофа 2009 г.

5. «Пособие по математике для поступающих в ВУЗы» под редакцией Г. Н. Яковлева. М. Наука 1985г.

6. «Задачи по элементарной математике» В. Б. Лидский. М. Наука 1973г.

7. «Справочник по математике» В. А. Гусев, А. Г. Морлкович. М. Просвещение 1995г.

8. «Математика» В. Т. Лисичкин, И. Л. Соловейчик. М. Высшая школа 1991г.

9. «Справочник по математике для средней школы» под редакцией С.А. Степанова. М. Наука 1980г.

10. «Элементарная математика повторительный курс» под редакцией В. В. Рыжакова. М. Наука 1974г.

11. «справочник по математике (для научных сотрудников и инженеров) Г.Корн, Т.Корн» перевод со второго американского переработанного издания И.Г. Арамановича, А.М. Березмана, И.А. Вайштейна, Л.З Румшинского, Л.Я.Цлафа по общей редакцией И.Г.Арамановича, М.Наука 1978г

Название учебно-исследовательской работы  «Умножение с увлечением или альтернативные приёмы умножения»

Автор работы Тукузов Кирилл Андреевич, 5 класс

Образовательное учреждение, в котором обучается автор(ы) работы МОУ «Средняя школа № 27» г. Саранск Республика Мордовия

Руководитель: учитель начальных классов МОУ «Средняя школа  № 27» Терлецкая Наталья Владимировна

Научный руководитель: кандидат психологических наук, доцент кафедры писихологии МГПИ им. М. Е. Евсевьева

                                                                             Лезина Светлана  Васильевна                                                                                                    

Цель данной работы: изучить нестандартные способы умножения и экспериментальным путем доказать целесообразность и эффективность использования рациональных способов  при выполнении математических заданий в школе и дома.

В соответствии с поставленной целью были определены задачи:

1. Найти как можно больше нетрадиционных способов умножения. Выбрать для себя наиболее рациональные и научиться их применять.
2. Исследовать скорость и точность нахождения произведения многозначных чисел у учащихся 4-10 классов. Узнать используют ли школьники нашей школы приемы альтернативного умножения.
3. Провести формирующий эксперимент с помощью мастер-класса по изучению приемов быстрого счета в 4-10 классах. И на конкретных примерах показать преимущества их использования.

При выполнении работы были использованы различные методы: поисковый, исследовательский, практический, опрос, анкетирование, беседа.

В теоретической части рассматриваются разнообразные способы умножения: общие и специальные,  выявляются наиболее рациональные из них.

В практической части экспериментальным путём доказывается эффективность использования рациональных способов  при выполнении математических заданий в школе и дома.

Значимость и прикладная ценность данного исследования заключается в том, что изучение альтернативных способов умножения и применение наиболее рациональных из них позволяет считать быстро и правильно. А процесс выполнения умножения сделать не только полезным, но и интересным.

Актуальность данной работы состоит в том, что в наше время все чаще на помощь ученикам приходит калькулятор в телефоне, на компьютере, и все большее количество детей не может правильно и быстро считать, не используя технические средства. А ведь умение считать необходимо современному человеку.

Анализ результатов экспериментов позволил сделать вывод об эффективности применения рациональных (альтернативных) приемов умножения.

При написании работы были использованы книги Кетлер Э.и Мак-Шейн Р. «Система быстрого счета по Трахтенбергу», Перельман М.Я. «Занимательная арифметика», Хэндли Б. «Считайте в уме как компьютер», учебники математики и Интернет.

Название учебно-исследовательской работы «Великаны в мире чисел»

Автор работы Тукузов Кирилл Андреевич, 5 класс

Образовательное учреждение, в котором обучается автор(ы) работы МОУ «Средняя школа № 27» г. Саранск Республика Мордовия

Руководитель: учитель начальных классов МОУ «Средняя школа № 27» Терлецкая Наталья Владимировна

Научный руководитель: кандидат психологических наук, доцент кафедры психологии МГПИ им М.Е. Евсевьева Лезина Светлана Васильевна

Цель данной работы: изучить числа – великаны, узнать их назначение и применение.

Задачи: 1. Выяснить какие числа называются великанами. Научиться составлять, записывать и читать числа-великаны. 2. Выяснить, где в окружающем нас мире, могут встретиться числа – великаны (В каких научных отраслях и в практической деятельности человека используются огромные числа). 3. Провести опрос и выяснить, насколько хорошо учащиеся нашей школы знают числа-великаны. 4. Найти и составить самому задачи с использованием больших чисел.

Гипотеза: я предположил, что числа – великаны не нужны современным школьникам, потому что они нигде не встречаются с ними.

Познакомившись с миром чисел-великанов, я целенаправленно стал искать встречи с ними. Оказалось, числа-великаны повсюду. Они встречались в легендах и сказаниях, в живой и неживой природе. Я понял, что в своей повседневной деятельности мы сталкиваемся с ними очень даже часто. Поэтому я решил выяснить, знают ли числа-великаны школьники. Для этого я провел опрос учащихся 4 - 9 классов своей школы. Процент детей знакомых с числами-великанами был настолько мал, что мне захотелось познакомить всех желающих с ними. Поэтому я подготовил и показал презентацию «В мире числовых-великанов», а для отработки навыка по называнию больших чисел я составил информационный сборник «Числа великаны рядом с нами» и подготовил сборник задач.

Актуальность В школьном курсе «математика» тема «числа-великаны» не изучается. В то время как, встреча с ними нам неизбежно предстоит на уроках физики, астрономии, географии. Я решил расширить свой кругозор в употреблении и чтения многозначных чисел- великанов. Этим и обусловлен выбор моей темы.

Практическая значимость работы связана с тем, что изучение чисел-великанов позволит углубить наши знания в изучении математики, заглянув в прошлое мира чисел.

В ходе выполнения работы моя гипотеза не подтвердилась.

Вывод: современному школьнику необходимо знать большие числа, уметь их записывать и читать, так как числа-великаны встречаются всюду.

Источники информации: 1. Депман И. Я., Виленкин Н.Я. За страницами учебника математики: пособие для учащихся 5-6 классов средней школы. М. Просвещение,1989.-287с. 2. Депман И. Я. Мир чисел. М.: Детская литература,1982.-160с. 3. Кординский Б. А.,Ахадов Л. А.Удивительный мир чисел: книга для учащихся. М.Просвещение,1986.-144с. 4. Литцман В. Великаны и карлики в мире чисел. М,1959. 5. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. М. Просвещение, 1988.-160с. 6. Перельман Я.И.. «Живая математика». Издательство «Наука», Москва, 1970 г. 7. Перельман Я. И. «Загадки и диковинки в мире чисел»

1. Название научно-исследовательской работы: «Как оптимально выбрать поставщика с помощью теории игр»
2. ФИО автора работы: Акуловский Даниил Валерьевич
3. Образовательное учреждение, в котором обучается автор работы: МБОУ «Гимназия имени А.Н.Островского» городского округа Кинешма
4. ФИО, должность и место работы научного руководителя: Шалободова Лариса Анисимовна, учитель математики МБОУ «Гимназия имени А.Н.Островского» городского округа Кинешма
5. Краткая постановка цели и задач исследования:

Цель данной работы: исследование применения теории игр при оценке качества проведения аукционов на поставку товаров и услуг для нужд организаций.

Задачи исследования:

- рассмотреть действующий порядок определения поставщиков товаров и услуг;

- выявить недостатки имеющихся методик;

- предложить практику применения элементов теории игр для совершенствования существующих процедур.

1. Основной текст тезисов.

В данной работе кратко описано место игр в нашей жизни. С  этой целью сделан экскурс в историю увлекательного раздела математики теории игр, рассказано о выдающихся ученых, своими работами создавших новое направление в математике, а также о современном состоянии теории игр и приведены примеры использования теории игр в экономике.

Для достижения поставленной цели в работе сформулирована проблема выбора поставщика товаров и услуг для нужд организаций, описаны правила, выявлены и определены недостатки действующей системы. Для общего понимания, рассказана классическая задача «Дилемма заключенных», приведено ее решение и дано определение ключевого параметра «равновесия Нэша». В ходе проведенного исследования сделаны допущения при решении реальной ситуации и предложен метод теории игр для оценки качества проведения тендеров.

Сформулированы вывод для оценки правильности и предложения по совершенствованию действующей системы выбора поставщика. Опубликован краткий обзор литературы, использовавшейся при подготовке этой работы.

1. Актуальность исследования обуславливается непростой экономической ситуацией, сложившейся в стране, вынуждающей искать способы наиболее эффективного использования средств.
2. Значимость и новизна исследования.

Значимость исследования подтверждается тем, что выводы и положения настоящей работы могут послужить основой для последующего применения предложенных математических методов.

Новизна исследования заключается в особом подходе к рассмотрению показателя равновесия Нэша. В классической задаче выбираются оптимальные стратегии для игроков, а в данной работе определена методика выбора оптимальной стратегии устроителя аукциона, то есть решается задача обратная классической.

1. Итоги исследования.

В рамках проведенного исследования выявлены и описаны существенные недостатки действующих систем проведения аукционов, которые приводят к неэффективному расходованию средств государственного бюджета и организаций. Для совершенствования сложившегося порядка, предложен дополнительный механизм контроля качества проведения торгов, который заключается в применении математических методов, изложенных в теории игр.

1. Список использованной литературы

1) Дж. фон Нейман, О. Моргенштерн. «Теория игр и экономическое поведение», Наука, 1970.

2) Замков О.О., Толстопятенко А.В., Черемных Ю.Н. «Математические методы в экономике», Москва 1997, изд. «ДИС».

3) Оуэн Г. «Теория Игр», Москва, Мир, 1970.

4) http://ru.wikipedia.org/wiki

5) Писарук Н.Н. «Введение в теорию игр», Минск, 2015

6) Авинаш Диксит, Барри Дж. Нейлбафф «Теория игр. Искусство стратегического

мышления в бизнесе и жизни», Москва, Манн, Иванов и Фербер, 2015

7) Федеральный закон от 05.04.2013 N 44-ФЗ "О контрактной системе в сфере закупок товаров, работ, услуг для обеспечения государственных и муниципальных нужд" .

Программное обеспечение для кассового аппарата, разработанное в среде программирования Delphi 7

Плетнев Тимофей Сергеевич

ГОУ «Забайкальский краевой лицей-интернат» , 8 класс

Бекетова Ольга Анатольевна, учитель информатики первой квалификационной категории

ГОУ «Забайкальский краевой лицей-интернат»

Целью является разработать ПО для кассового аппарата

Задачи:

• Изучить литературу по заданной теме
• Создать интерфейс ПО
• Запрограммировать ПО
• Предоставить проект на конференцию

План работы:

• Изучить Базы Данных Microsoft Access, Delphi 7;
• Научиться взаимодействовать с Базами Данных в Delphi 7;
• Научиться обмениваться информацией между Базами Данных;
• Создать интерфейс для будущего ПО;
• Прописать программные коды;
• Научиться взаимодействовать с компонентами для печати;
• Подключить к ПО сканер штрих-кодов;
• Исправить все недочеты и баги ПО;

Актуальность: вопросы автоматизации процессов поиска, обработки, приема, передачи, сортировки и хранения данных ставятся довольно остро в условиях информационного общества, поэтому возможность создания программного обеспечения для кассовых аппаратов в среде объектно-ориентированного программирования Delphi 7 в связке с использованием СУБД Microsoft Access позволяет качественно решить эти вопросы;

Значимость и новизна исследования: данное программное обеспечение может применяться для обработки и сортировки большого количества данных в условиях экономического предприятия; разработчику неизвестны случаи разработки программного обеспечения для кассового аппарата школьниками;

Главное меню программы:

Окно с базой данных (открывается по нажатию кнопки "База Данных"):

Окно добавления нового продукта в базу данных (при нажатии кнопки "Добавить продут"):

9.Итог исследования: ПО для кассового аппарата создано;

10. Список литературы: http://www.cyberforum.ru/

Рванова Людмила Юрьевна, 11 класс, областная специализированная школа-лицей для одаренных детей ЛОРД, г. Петропавловск, Республика Казахстан

Руководитель: Грызов Иван Валентинович, учитель информатики областной специализированной школы-лицея для одаренных детей ЛОРД

Актуальность исследования. В современное время в астрономии широко используются телескопы, снабженные матрицами для цифровой фиксации результатов наблюдения. Эти телескопы снабжены системой гидирования, позволяющей получать изображение одного участка звездного неба с высокой точностью позицирования. Полученные серии фотографий позволяют определить временные изменения яркости астрономических объектов, находить объекты, меняющие свои координаты на звездном небе (спутники, метеоры и т. п.), оценивать влияние атмосферы на наблюдения. В связи с вышесказанным, актуальной является задача создания программных средств, автоматизирующих решения подобных задач. В нашем распоряжении оказались серии фотографий участков звездного неба созвездия Кассиопеи через равные промежутки времени на телескоп «Halfman», расположенный в обсерватории гимназии «Самопознание» фонда «Бобек», г. Алматы (рис. 3).  Перед нами была поставлена задача автоматизированного нахождения объектов с переменной яркостью на данных сериях фотографий.

Цель исследования: разработка и апробация системы анализа динамики светимости переменных звезд на основе алгоритмов компьютерного зрения.

Для реализации цели нами были поставлены следующие задачи.

1. Изучение теоретического материала, связанного с переменными звездами.
2. Ознакомление с алгоритмами обработки фотографий звездного неба.
3. Разработка системы для обработки серий фотографий одного участка неба.
4. Пробная эксплуатация системы и анализ полученных результатов.

Значимость и новизна исследования. Автоматизирован процесс нахождения переменных звезд на участке звездного неба по серии фотографий. Созданное программное обеспечение может быть применено в астрономических обсерваториях для решения задачи поиска звезд переменной яркости. 

Координатная система на фотографиях взята внутренняя, так как мы не имеем достаточного количества информации для привязки к небесной системе координат.

В процессе работы нами был выработан следующий алгоритм обработки полученной серии фотографий.

1. Удаление шума.
2. Обнаружение объектов, определение координат точек с наибольшей яркостью.
3. Сравнение яркостей объектов с аналогичными координатами на других фотографиях.

Имеющиеся в нашем распоряжении фотографии довольно хорошего качества, но с высоким уровнем шума, который необходимо удалить, иначе система примет этот шум за звезду и будет работать некорректно. Для удаления шума мы берем первую фотографию и переводим ее в черно-белый формат пороговым методом (рис. 4).

Нами был использован следующий алгоритм обнаружения объекта.

1. Перевод изображения в ч/б с удалением шума.
2. Сканирование изображения в вертикальном направлении.
3. После нахождения белой точки осуществление поиска в горизонтальном направлении в обе стороны и нахождение границ светлой области.
4. Поиск границ области в вертикальном направлении.
5. Нахождение координат центра полученной прямоугольной области.

По сути, нашей задачей является «окружение» изображения звезды прямоугольной оболочкой и нахождение центра этой области (рис. 5). Нахождение звезд производится на обработанной копии первой фотографии. Координаты звезд запоминаются и далее применяются для нахождения яркостей на каждой фотографии.

Полученные данные (рис. 6) обрабатываются написанной нами программой на языке Object Pascal с целью получения среднего значения и максимального отклонения, отбрасываются звезды с малым процентом отклонения от средней яркости. Взятые условные единицы яркости переводятся в логарифмическую шкалу. Для создания программы использована среда разработки Lazarus (рис. 7, 8).

Итоги исследования. В процессе пробной эксплуатации на основе имеющихся исходных данных были сделаны следующие выводы.

1. На основе имеющихся в нашем распоряжении средств разработки с открытым кодом возможно создание программного обеспечения для обработки астрономических фотографий.
2. Выбранные алгоритмы и технические решения показали достаточно высокую эффективность и скорость работы.
3. Большое влияние на результат обработки оказывает качество исходного материала, а также погодные условия в месте наблюдения.
4. К сожалению, из-за отсутствия временной разметки в исходных фотографиях можно говорить лишь о возможности оценки вероятности того, что звезда является переменной, но созданная программа позволяет отобрать звезды-кандидаты для дальнейшего исследования.

Созданное программное обеспечение может быть использовано в астрономических обсерваториях для решения задачи поиска звезд переменной яркости по серии фотографий участка звездного неба. 

Cписок литературы

1. Переменные звезды. Классификация и характеристики. – http://innotechnews.com/reviews/615-peremennye-zvjozdy-klassifikatsiya-i-kharakteristiki (Актуальная дата 10.10.2015).
2. А. В. Засов. Глоссарий. – Astronet.ru. http://www.astronet.ru/db/msg/1188527 (Актуальная дата 23.09.2015).
3. Кононович Э.В., Мороз В.И. Общий курс астрономии. М.: Едиториал УРСС, 2004.
4. Алексеев Е.Р. FreePascal и Lazarus. Учебник по программированию. М.: ALT Linux; Издательский дом ДМК-пресс, 2010.
5. Алексеев Е.Р., Чеснокова О.В., Кучер Т.В. Самоучитель по программированию на Free Pascal и Lazarus. – Донецк: ДонНТУ, Технопарк ДонНТУ УНИТЕХ, 2009.
6. Документация по Lazarus. – http://www.lazarus-ide.org/ (Актуальная дата 25.09.2015).
7. Документация по ImageMagik. – http://www.imagemagick.org/ (Актуальная дата 25.09.2015).

Олимпиадные задачи на время и даты

г. Красноярск, МБОУ Гимназия №9, 9 класс

руководитель: Шавонина Светлана Тимофеевна, МБОУ Гимназия № 9, учитель математики

Исследовательская работа посвящена изучению олимпиадных задач (задач повышенного уровня сложности). Методы: поиск, анализ решений и ответов на задачи, конспектирование, реферирование, количественный анализ результатов, анализ литературы, классификация задач, решений и ответов по типам, метод сравнительно-сопоставительного анализа, описательный метод, оценочный метод.

Государственное бюджетное общеобразовательное учреждение

Гимназия №107  

От точи до симплекса

Исследовательская работа по математике

Выполнил ученик 9-1 класса

Владимир Гладштейн

Руководитель :

Мамаева Т.А., учитель математики

Санкт-Петербург

2015-2016

Актуальность

Моя исследовательская посвящена многомерной геометрии Евклида. В основном четвёртому измерению. Это тема была и остаётся очень популярной. Людей всегда влекло всё неизвестное.

Вы, конечно, скажете, что это четвёртое измерение нереально. Оно надуманно и не имеет практического смысла. Но у меня есть один веский аргумент. В истории математики было много разных тем, которые казались «пустыми»: неевклидова геометрия, кватернионная алгебра, комплексные числа вообще…. Но я вам расскажу о неевклидовой геометрии. Я предполагаю, что все слышали это словосочетание. Все знают, что создатель первой неевклидовой геометрии был Николай Иванович Лобачевский. Но мало кто знает, что из-за этой геометрии он умер в нищете. Н.И. Лобачевский был ректором казанского университета, и когда он представил свои труды по поводу новой геометрии высшему математическому сообществу, ему посмеялись в лицо и уволили. Прошло много лет и словосочетание неевклидова геометрия у всех на слуху. И ассоциируется оно с именем величайшего русского математика Николая Ивановича. Но почему она стала так известна? Всё просто, появились новые технологии, новые знания, которые выходили за рамки геометрии Евклида, и до людей дошло, каким гением был Лобачевский. Мораль сей басни такова: в математике даже в самых абсурдных темах может крыться нечто поистине великое.

На тему: «как устроено четвёртое измерение» было придумано очень много гипотез. Когда придумывать стало уже нечего, люди взялись за описание геометрических объектов в этом измерении. Очень подробно была исследована самая простая геометрическая фигура- куб.

Я взялся исследовать другую фигуру, которой уделили не так много времени- тетраэдр (треугольную пирамиду).

Как тетраэдр выглядит в четвёртом измерении?

Как можно его себе представить?

Можно ли вычислить его четырёхмерный объём?

На эти и другие вопросы вы найдёте ответы ниже

Цель

Исследовать гипертетраэдр

Задачи

Задачи

Построить тетраэдр в:

• 0-лимерном
• 1-номерном
• 2-ухмерном
• 3-ёхмерном

пространстве

Создать:

• развёртку четырёх мерного тетраэдра
• Проекцию четырёхмерного тетраэдра на трёхмерное пространство
• Написать формулы для вычисления разных величин для гипертетраэдра со стороной а

 Значимость и новизна исследования

Представлен аналог тетраэдра во всех измерениях

В нулимерном- точка.

В одномерном- отрезок.

В двумерном- треугольник.

В трёхмерном- тетраэдр.

Созданы: тень и развёртка гипертетраэдра, рассчитаны: его гиперобъём, радиус вписанной и описанной гиперсферы, высота гипертетраэдра и угол между двумя гранями.

Алгоритм действий.

Для вычисления аналогов тетраэдра в 0-3мерном измерении, использовалось сечение тетраэдра n-мерным пространством.

Для четвёртого измерения использовались аналогии с 0-3мерного измерения. Гиперобъём был вычислен двумя способами, одним из которых было- интегрирование (я взял тройной интеграл, модифицировал его в четверной и взял)

Выводы

• Получена развёртка симплекса
• Получена тень симплекса
• Получено много формул для вычисления гипервеличин в симплексе. В ходе чего, был применен новый вид интеграла.
• Выявлен закон изменения количества элементов в n-мерном тетраэдре при добавлении ещё одной размерности.
• Выявлено, что этот таблица количества элементов в n-мерном тетраэдре совпадает с треугольником Паскаля.
• Прослежена эволюция тетраэдра: от точки до симплекса.

Список литературы

1. Рауль Ибаньес. Четвёртое измерение., «Deagnostini». 2014.
2. http://mathprofi.ru/ О образовательный сайт по математике
3. Александров П. С. Комбинаторная топология, М. — Л., 1947.
4. Понтрягин Л. С. Основы комбинаторной топологии, М. — Л., 1947, С. 10—46
5. Выгодский М.Я. Справочник по высшей математике. «Наука». 1976. С. 17-529
6. https://msdn.microsoft.com/ru-ru/windows/hardware/bg183398 руководство по программе 3D Builder
7. Анастасян Л.С. Бутузов В.Ф. Камодцев С.Б. Позняк Э.Г. Юдина И.И. Геометрия. Учебник для 7-9 классов. С. 31-34. 125-128. 158-175. 149-156.
8. Селиванов Д. Ф., Тело геометрическое // Энциклопедический словарь Брокгауза и Ефрона: в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
9. Матизен В.Э. Равногранные и каркасные тетраэдры «Квант» № 7, 1983 г.

Автор: Кулаков Константин Сергеевич, 11 класс, МБОУ «Лицей №129», г. Барнаул, Алтайский край

Научный руководитель: Рыжова Ирина Михайловна, учитель информатики, МБОУ «Лицей №129»

Актуальность работы: в настоящее время в различных областях человеческой деятельности все шире применяются технологии компьютерного зрения. В данной работе рассматривается распознавание автомобильных номеров, которое актуально для автоматизации работы государственных органов безопасности дорожного движения, полиции, охранных организаций.

Объект исследования: методы распознавания изображений.

Предмет исследования: процесс обнаружения и распознавания автомобильного номера на цифровых изображениях с использованием метода Виолы-Джонса

Цель: разработка библиотеки, реализующей автоматическое распознавание российских автомобильных номеров.

В работе представлено применение методов автоматизации распознавания автомобильных номеров на примере разработки собственной библиотеки, предоставляющей функционал для распознавания российских автомобильных номеров, приведено математическое обоснование работы метода. Автором описаны основные этапы применения метода Виолы-Джонса для поиска области с автомобильным номером. Для поиска объекта на цифровом изображении используется обученный классификатор, представленный в формате xml. Классификатор формируется на примитивах Хаара. Ознакомиться с процессом обучения каскада Хаара можно в статье, опубликованной автором в личном блоге http://kostyakulakov.ru/2015/07/04/opencv-обучение-каскада-хаара/

Разработаны и реализованы собственные алгоритмы поиска и нормализации угла наклона автомобильного номера, поиска верхней, нижней и боковых границ автомобильного номера, гистограммного анализа, нормализации и выделения связанных областей в изображении и распознавания найденных символов.Для распознавания символов автором было принято решение использовать готовый, проверенный временем продукт от компании Google –TesseractOCR. Библиотека для распознавания символов TesseractOCR использует нейронную сеть, обучение которой автор произвел с учётом шаблонов символов автомобильного номера и научил работать библиотеку с номерами, которые имеют мелкие помеховые составляющие. Технология сборкиTesseractOCR под компилятор mingw32 была разработана автором, проверена на практике и описана в статье, опубликованной на крупном Интернет-ресурсе http://habrahabr.ru/post/262483/.

В работе описаны разработанные автором основные методы библиотеки, позволяющие автоматизировать процесс распознавания российских автомобильных номеров. Библиотека находится в открытом доступе в крупной системе контроля версий.

Апробация библиотеки в реальных условиях наглядно демонстрирует работоспособность применённых методов автоматического распознавания российских автомобильных номеров.
 Дальнейшее развитие проекта включает улучшение работы алгоритма отсечения помеховой составляющей изображения.

Значимость и новизна: Анализ программных продуктов по распознаванию автомобильных номеров показал, что в настоящее время на рынке представлены библиотеки, либо не обеспечивающие требуемое быстродействие, либо не учитывающие угол наклона номера, что послужило основой исследования.

Итоги исследования: разработана библиотека реализующая распознавание российских автомобильных номеров с учётом угла наклона и помеховой составляющей. Успешно апробирован продукт разработанный с использованием данной библиотеки

Список использованной литературы

1. A Real-Time Mobile Vehicle License Plate Detection and Recognition Kuo-Ming Hung and Ching-Tang Hsieh: гистограммный подход при распознавании номеров  [Электронный ресурс]. URL:  http://www2.tku.edu.tw/~tkjse/13-4/09-IE9722.pdf (дата обращения 20.08.2015)
2. Automated Number Plate Recognition Using Hough Linesand Template MatchingSaqib Rasheed, Asad Naeemand Omer Ishaq:  поиск номеров через HOG-дескрипторы вертикальных линий [Электронный ресурс]. URL: http://www.iaeng.org/publication/WCECS2012/WCECS2012_pp199-203.pdf(дата обращения 21.08.2015)
3. Survey of Methodsfor Character RecognitionSuruchi G. Dedgaonkar, Anjali A. Chandavale, Ashok M. Sapkal:  небольшая обзорная статья про распознавание букв и цифр [Электронный ресурс].  URL:  http://ijeit.com/vol%201/Issue%205/IJEIT1412201205_36.pdf (дата обращения 20.08.2015).

Автор:Афанасейкин Александр Михайлович, 11 класс, МБОУ «Гимназия №40» имени Народного учителя СССР ОвсиевскойРуфины Серафимовны,город Барнаул, Алтайский край

Научные руководители:Мальцев Юрий Николаевич, доктор физико-математических наук, профессор Алтайского государственного педагогического университета и

Лупина Светлана Юрьевна, учитель математики,МБОУ «Гимназия №40».

Целью нашей работы стало исследование разности , где тройки чисел {x,y,z} и {u,v,w} принимают значения некоторых параметров ∆ABC; а точнее – нахождение оценок сверху и снизу для таких разностей  через основные параметры  p, R, r.

Вопрос о соотношениях между длинами высот, сторонами некоторого треугольника, радиусами вписанной, описанной и вневписанной окружности и косинусами, тангенсами и котангенсами углов данного треугольника в научной литературе рассматривался недостаточно широко. Поэтому исследование разности  для троек чисел {x,y,z} и {u,v,w}, принимающих значения некоторых параметров треугольника, с нашей точки зрения является актуальным и требующим завершенности в нахождении оценок сверху и снизу для таких разностей  через основные параметры p, R, r.

Для проведения исследований по теме были использованы следующие методы: анализ результатов из книги В.П. Солтан, С.И. Мейдман «Тождества и неравенства в треугольнике», книги Д.О. Шклярский, Н.Н. Ченцов, И.М. Яглом «Избранные задачи и теоремы элементарной математики» (часть I, арифметика и алгебра) и собственные математические рассуждения.

В ходе проведенных исследований были доказаны семь теорем, четыре леммы, три следствия.

Полученные нами результаты в работе являются новыми (ранее не встречались в известной для нас литературе). Их можно использовать в работе математических кружков и для дальнейшего исследования геометрии треугольника.

 Литература

1. Мейдман С.И., Солтан В.П. «Тождества и неравенства в треугольнике», Кишинев, изд-во «Штиинца», 1982
2. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. «Избранные задачи и теоремы элементарной математики», часть I (арифметика и алгебра), Москва, Гос. изд-во ФМЛ, 1959

Автор: Жуганов Михаил Юрьевич, 10 класс, МБОУ «Гимназия №40» имени Народного учителя СССР Овсиевской Руфины Серафимовны, город Барнаул, Алтайский край

Научные руководители: Мальцев Юрий Николаевич, доктор физико-математических наук, профессор Алтайского государственного педагогического университета и Белоцкая Юлия Николаевна, учитель математики, МБОУ «Гимназия №40».

 В известной книге по геометрии треугольника (С.И. Зетель, Новая геометрия треугольника, г. Москва, 1962 г., с. 39 и с. 42) доказаны следующие утверждения:

1. Если через центр тяжести треугольника провести прямую, то сумма расстояний от этой прямой до двух вершин треугольника, находящихся от неё по одну сторону, равна расстоянию от этой прямой до третьей вершины;
2. Если через центр вписанной окружности провести прямую и на неё из вершин треугольника опустить перпендикуляры, то ad_A+bd_B+cd_C= 0, где a=BC,b=AC, c=AB – длины сторон∆ABC, и сумма берётся с учётом направлений отрезков.

Целью настоящей работы является обобщение указанных результатов для прямых, проходящих через точку пересечения произвольных чевиан треугольника.

Актуальность данной темы обусловлена тем, что в геометрии накоплен значительный материал о свойствах прямых, проходящих через замечательные точки треугольника. Этот материал необходимо осмыслить, структурировать, обобщить и представить, как совокупность знаний об этих удивительных прямых и их свойствах.

В качестве следствий доказанной в работе теоремы получены неожиданные алгебраические соотношения для длин перпендикуляров d_A, d_B, d_C, опущенных из вершин ∆ABC на произвольную прямую, проходящую через замечательные точки∆ABC.

Также в качестве следствия получено новое доказательство того, что точки O, G, N лежат на одной прямой (т. н. ″2-й прямой Эйлера″).

Научная новизна

Полученные результаты являются новыми, ранее не встречающиеся в известной нам литературе.

Итоги исследования

Полученные в работе результаты, а также выведенная общая формула алгебраической зависимости величин (длин перпендикуляров) , опущенных из вершин A, B, C на произвольные чевианы ∆ABC, полезны для дальнейшего исследования геометрии треугольника.

Список литературы

1. Ефимов Н. В., «Краткий курс аналитической геометрии»,г.Москва, 1975 г.
2. Зетель С. И., «Новая геометрия треугольника», Учпедгиз , 1962 г.
3. Скопец З. А., Жаров В.А., «Задачи и теоремы по геометрии (планиметрия)», Москва, 1962 г.

Исследовательская работа «Нега-позиционные системы счисления»

Выполнила: Каляева Ангелина Владимировна. г.Арзамас МБОУ «Лицей»

Руководитель: Мурзина Ольга Ивановна. Учитель информатики МБОУ «Лицей»

Цели работы:

• Исследовать особенности алгоритмов перевода чисел из нега-позиционных систем счисления и в нега-позиционные системы счисления;
• Сравнить с привычными нам алгоритмами переводов для известных нам системам счисления.
• Выяснить, существует ли возможность определения по количеству цифр в нега-позиционной системе счисления является ли число положительным или отрицательным в привычной нам десятичной системе счисления.
• В случае ошибочности нашей гипотезы выдвинуть и обосновать новые правила перевода для нега-позиционных систем счисления.
• Выяснить область применения нега-позиционных систем счисления в современных условиях.

Алгоритм перевода из нега-позиционной системы счисления в десятичную систему счисления полностью совпадает с изученным нами в школе алгоритмом, т.е. правило перевода из любой системы счисления в десятичную посредством разложения на разрядные слагаемые является универсальным.

«Правило количества цифр»: Если в записи числа в нега-позиционной системе счисления количество цифр четное, то в десятичной системе счисления ему соответствует отрицательное число. И наоборот, если в записи числа в нега-позиционной системе счисления количество цифр нечетное, то в десятичной системе счисления ему соответствует положительное число.

В данной работе мы постарались обосновать, выведенное нами правило.

Рассмотрев несколько примеров, мы убедились, что обычное правило перевода  из десятичной системы не работает для нега-позиционный систем счисления.

      Правило перевода из десятичной системы в нега-позиционную систему счисления: при переводе чисел из десятичной системы счисления в нега-позиционную систему счисления необходимо число, записанное в десятичной системе счисления, делить на отрицательное основание до тех пор, пока это возможно, причем, если делимое число отрицательное, то получаемое частное необходимо брать на единицу больше, чем получается по обычным правилам. После окончания деления необходимо записать остатки от деления справа налево (или снизу вверх), полученное число и является записью исходного числа в нега-позиционной системе.

       Актуальность, значимость и новизна исследования

Мы считаем, что наша работа является на сегодняшний день самой полной по исследованию алгоритмов перевода чисел из и в нега-позиционные системы счисления. Значимость нашей работы заключается в расширении горизонтов познания школьников и студентов в плане углубления знаний по математическим основам информатики. Попытка получить универсальный алгоритм перевода из десятичной системы счисления в любую другую, включая нега-позиционную, впервые получила свое логическое завершение, проверку и преобразование в программный код.

       Итоги исследования: В завершении работы, мы сформулировали обобщенные правила перевода из любой системы счисления с целым основанием в десятичную систему счисления и обратно. К работе мы прилагаем программный код на языке Паскаль, который реализует перевод из любой системы счисления (включая нега-позиционные) в любую другую (включая нега-позиционную) в диапазоне оснований системы счисления от -16 до +16.

Используемая литература:

1. Grunwald Vittorio. Giornale di Matematiche di Battaglini.1885, p. 203-221, 367.
2. Столяров И.В. Научные аспекты проектной деятельности учащихся по информатике. - Материалы Всероссийской научно-практической конференции «Прикладная информатика и компьютерное моделирование». – Уфа: БГПУ им. М. Акмуллы, 2012, с. 29 – 31.
3. Емельянова А. Нега-позиционные системы счисления. XIII Школьные Харитоновские чтения. Саров: ФГУП «РФЯЦ-ВНИИЭФ», 2013, Научный руководитель Столяров И.В.

Тезисы

1.  Пространственная симметрия у живых организмов
2. ФИО автора: Майоров Александр Игоревич, ученик 9 класса, МОУ Дмитровская гимназия «Логос»
3. МОУ Дмитровская гимназия «Логос»
4. ФИО руководителя: Майорова Елена Георгиевна, учитель математики, ГБОУ ЦО № 1296 г.Москва

Харитонова Марина Александровна, учитель математики, МОУ Дмитровская гимназия «Логос»

5. Целью исследовательской работы является расширение сферы математических знаний и анализ основных особенностей симметрии в биологии. Для достижения поставленной цели в работе решаются задачи:

- рассмотреть понятие и виды симметрии;

- изучить проявления симметрии в живой природе;

- проанализировать и выявить особенности симметрии листа комнатного растения и кистей рук человеческого тела.

5 Методы исследования: анализ теоретической и методической литературы, морфометрический метод, методы статистической обработки результатов исследования.

6. Зная симметрию биообъектов, возможно прогнозирование их развития. Именно данными аспектами и обусловлена актуальная значимость выбранной темы.

7. Исследовательская работа обладает практической направленностью. Так, практическая значимость исследования пластины листа растения заключается в том, что представлена возможность применения морфометрических методов для оценки качества окружающей среды. Наиболее чувствительным органом растений является зеленый лист, он подвержен действию токсических газов. Фиксация и оценка морфометрических параметров листьев городских растений даст достоверную картину состояния городской среды. Биомониторинг - эффективный и недорогой метод, надежный индикатор загрязнения  среды различными токсическими веществами.

            Биометрические технологии, включающие анализ симметрии кистей рук человека, используются в настоящее время для обеспечения безопасности и идентификации людей. Практическая значимость данного направления исследований - в диагностике и лечении заболеваний человека.

8. Симметрия пространства доступна нашему обыденному восприятию. Ее виды нашли свое отражение во внешнем строении растений, животных, в конструкции их внутренних органов, в конфигурации молекул органических веществ.

           В данной проектной работе, в очередной раз доказаны известные слова Ф. Дайсона: «Жизнь – это нарушение симметрии. Мы не можем ответить на вопрос, что такое жизнь, но имеем способ отличить живое от неживого. Асимметрия – это разграничительная линия между живой и неживой природой».

Список литературы:

1.  Биометрические технологии: геометрия руки. Материалы подготовлены ИИЭИЭ в рамках проекта «Попробуй себя инженером». www.tryengineering.org
2. Вейль Г. Симметрия. М.: Едиториал УРСС, 2007.
3. Вернадский В.И. Химическое строение биосферы Земли и ее окружения. М., 1965.
4. Гильде В. Зеркальный мир. — М.: Мир, 1982г.
5. Грядовой Д.И. Концепции современного естествознания. Структурный курс основ естествознания. – М.: Учпедгиз, 1999.
6. Дмитриев И.С. Симметрия в мире молекул. Л., «Химия», 1976.
7. Дубнищева Т.Я. Концепции современного естествознания. – Новосибирск: ЮКЭА, 1997.
8. Ермоленко А., Перепада Е. Двухполостная симметрия человека. М.: Учпедгиз, 2004.

Трёхмерная визуализация атмосферных фронтов

Раффаэле Делла Пиетра
ГБОУ Лицей “Вторая школа”

Аннотация

В работе рассматривается визуализация сложных трёхмерных объектов (атмосферных фронтов). Визуализация может помочь вести метеорологические исследования.

Данная работа выполнялась под руководством научных руководителей Дединского И. Р. (преподаватель МФТИ)
и Гордина В. А. (сотрудник Гидрометцентра России).

Введение

Для изучения атмосферных фронтов метеорологи рассматривают получаемые со спутников двумерные горизонтальные сечения атмосферы с данными о расположении фронтов
и их силе. Такое представление не всегда может быть удобным, поэтому возникла идея выполнить эту работу. Целью работы является сборка по спутниковым данным трёхмерной поверхности фронта и её визуализация, которая облегчит работу метеорологам и поможет представить фронт не сечениями, а целиком как единую поверхность. Представленная работа также может быть полезна как при обучении для более быстрого восприятия фронтовой карты, так и для людей, не очень близких к метеорологии, но нуждающимся в этих знаниях.

В ходе работы потребовалось изучить технологии визуализации трёхмерных объектов, метод построения поверхности и способы оптимизации программы.

Технологии

Для реализации данной задачи была использована графическая библиотека Direct3D11 на ОС Windows.
Для внутреннего представления данных в видеопамяти была использована концепция трёхмерной текстуры.
Визуализация происходила посредством алгоритма Raymarching [1].

Построение поверхности и визуализация

Хранение данных в трёхмерной текстуре позволило воспользоваться аппаратной трилинейной интерполяцией для получения гладкой поверхности. Промежуток между двумя соседними слоями линейно интерполируется, что позволяет выразить интенсивность любой точки атмосферы между двумя слоями и отобразить фронты с нужной точностью.

Для визуализации данной трёхмерной текстуры был использован алгоритм Raymarching: из камеры выпускаются лучи, которые пошагово проходят через нужную область, и собирается информация о пересечёнными ими фронтами.

Оптимизация

Данные со спутника занимают значительный объём, и все они нужны визуализатору, поэтому работа
с программой на обычном компьютере была бы некомфортно медленной.
По этой причине одной из главных задач было максимально оптимизировать скорость визуализации
для возможности работы в реальном времени. В текстуру передаётся минимальное возможное количество данных – только интенсивность точек, а на графическом процессоре происходит перевод интенсивности точки в её цвет и дальнейшая визуализация.

Заключение

В результате работы были рассмотрены технологии визуализации трёхмерных поверхностей с использованием технологии Direct3D11, была реализована визуализация атмосферного фронта.
Сотрудничество с Гидрометцентром позволяет постоянно обновлять локальные задачи, работа над проектом продолжается.

Актуальность

Проект представляет собой гибкую и доступную возможность расширить ресурсы сотрудников Гидрометцентра России, что может благоприятно повлиять на метеорологическую отрасль.

Литература

1. Гордин В. А. Математика, компьютер, прогноз погоды и другие сценарии математической физики.
2. http://www.stackoverflow.com

Ссылки

1. http://en.wikipedia.org/wiki/Volume_ray_casting

«Решение иррационального уравнения с параметром»

Выполнил Куляшов Влад Эдуардович

обучающийся 11 класса

МБОУ «Балезинская Средняя Общеобразовательная Школа №1»

Поселка Балезино, Удмуртская республика

Научный руководитель – Касимов Рифхат Шамилович

Учитель математики и физики МБОУ«Балезинская Средняя Общеобразовательная Школа №2»

Постановка проблемы.

Проблему исследования составляет поиск максимально большого количества всевозможных способов решения данного уравнения.

Степени их изучения в современном мире.

Эта проблема достаточно глубоко изучена в современной науке, но на уровне школьного курса математики изучено не достаточно, особенно на уровне программ для общеобразовательных школ, где преподавание математики и физики ведется не на профильном уровне.

Краткая характеристика источников.

Объект – иррациональное уравнение с параметром.

Предмет – поиск способов решения иррационального уравнения с параметром.

Цели исследования, его задачи.

Цель – найти как можно больше способов решения данного уравнения.

Задачи – подтвердить на практике решение данного уравнения максимально большим количеством способов.

Конкретизация выводов по каждой части докладов.

Мною найдено 8 способов решения данного уравнения, все они дают один результат, следовательно, они решены верно. Подтверждается обще известная истина о том, что математика, как и другие точные науки представляет из себя единую, композиционную взаимосвязанную систему, состоящую из отдельных направлений.

Общее заключение.

Мною найдено 8 способов решения данного уравнения, все они дают один результат, следовательно, они решены верно. Подтверждается обще известная истина о том, что математика, как и другие точные науки представляет из себя единую, композиционную взаимосвязанную систему, состоящую из отдельных направлений.

Список использованной литературы.

1) Г. В. Дорофеев «Пособие по математике для поступающих в вузы». Москва 1972 г.

2) И. Х. Сивашинский «Задачи по математике для внеклассных занятий». Москва 1968 г.

8-ая международная конференция научно-технических работ школьников «Старт в Науку»

Название научно-исследовательской работы: «Оптимизация производственных расписаний с помощью генетического алгоритма».

ФИО автора работы: Дерябин Иван Николаевич, 15.01.1999.

Образовательное учреждение, в котором обучается автор работы: ученик  10  класса МАОУ «Лицей №102 г. Челябинска»

ФИО, должность и место работы научного руководителя: Пашнин Андрей Александрович, педагог  дополнительного образования класса МАОУ «Лицей №102 г. Челябинска»

Краткая постановка цели и задач исследования.

Разработка программного комплекса способного сформировать оптимальное производственное расписание с помощью генетического алгоритма.

Основной текст тезисов. Краткое техническое описание проекта

В программе  задается набор работ , и исполнители.  Алгоритм должен оптимально распределить выполнение задач по исполнителям , чтобы суммарное время выполнение всех задач было минимальным.

В основе моделирования производственного расписания  лежит генетический алгоритм. Суть генетического алгоритма  заключается в следующем: отбирать наиболее подходящие решения и генерировать из них еще более оптимальные варианты на основе алгоритмов отбора, скрещивания и мутации. Так до тех пор, пока не будет найдено решение.  Задача сводилась к дискретной,  путём разбиения интервала времени на заданное количество  интервалов.   Для каждого интервала  определялась  загрузка  исполнителей.  В фитнес функции  суммировалась загрузка исполнителей  по всем интервалам  и учитывалось число переналадок исполнителей. Искался минимум фитнес функции.  Программный комплекс был реализован на языке Java,  данная среда разработки позволила создать дружественный интерфейс  и использовать преимущества  объектно ориентированного программирования.

Актуальность исследования.

Оперативное оптимальное   производственное планирование может существенно сократить  издержки при производстве продукции, так как  оно помогает сократить время  выполнения работ, эффективно загрузить  производственные мощности. Существующие программные   комплексы для оперативного производственного планирования,  как правило,  опираются на эвристические подходы поиска оптимальных расписаний, а значит,  могут работать не совсем эффективно и корректно при определенных ситуациях. Кроме того они очень дорогостоящи.

Именно поэтому целью нашей работы было создание доступной программы,  способной оперативно формировать  оптимальное производственное расписание на основе генетического алгоритма.

Итоги исследования.

Решены сформулированные задачи проекта:

1. Реализован генетический алгоритм поиска оптимального производственного расписания для задач без четкой иерархии.
2. Программа протестирована на различных вводимых данных. Алгоритм показал высокую сходимость для различный конфигураций, более чем на 100 тестах. Программа находила оптимальное решение менее чем за 15000 итераций.

В целом реализованный алгоритм показал хорошую сходимость к оптимальному результату и может быть использован для решения общей задачи оптимизации, в которой учитывалось бы иерархия задач, гибкая настройка мощности процессоров, цены переналадок оборудования и прочее.

Перспективы проекта:

1. Возможность задания иерархии задач (последовательности следования задач).
2. Увеличение размерности алгоритма (большое количество задач , интервалов времени).
3. Внедрение программного комплекса в реальное производство.
4. Совершенствование генетического алгоритма путем ускорения его работы с помощью методов параллельного программирования.

Исследовательский проект: "УСЛОВИЯ ОБОБЩЕНИЯ ФОРМУЛЫ ПИКА"

Бергер Никита Вячеславович

Муниципальное бюджетное общеобразовательное учреждение города Новосибирска Центрального района «Лицей №22 «Надежда Сибири»

Таранова Марина Владимировна, кандидат педагогических наук, доцент кафедры алгебры института физико-математического и информационно-экономического образования НГПУ.

Краткая постановка цели и задач исследования:

Найти рациональное решение задачи о площади фигуры, вершины которой лежат в узлах целочисленной решетки. Получить обобщение формулы Пика на объемные фигуры: прямоугольный параллелепипед и тетраэдр, вершины которых расположены в узлах трёхмерной целочисленной решётки.

Описание научно-исследовательской работы:

В научно-исследовательской работе находится применение формулы Пика в решении задач на вычисление площадей плоских фигур, вершины которых расположены в узлах решётки; исследуются условия, при которых формула Пика верна для трёхмерного случая: формула верна только для прямоугольного параллелепипеда. Были найдены условия вычисления объёма тетраэдра.

Актуальность, значимость и новизна исследования:

В экзаменационных материалах очень часто необходимо вычислить площадь плоской фигуры, вершины которой расположены в узлах целочисленной решетки. Очевидно, что наиболее рациональное решение подобных задач возможно с использованием специальной формулы Пика. Также выведенные мной формулы помогут найти площадь объемной фигуры.

Итоги исследования:

В ходе проекта мною изучены: понятия многоугольника с вершинами, расположенными в узлах целочисленной решётки; понятие связного многоугольника, теорема Пика; решены задачи на применение этой формулы.

Разрабатывая данную тему, я поставил и самостоятельно исследовал проблему обобщения формулы Пика на трёхмерный случай. Было показано, что формула верна только для прямоугольного параллелепипеда. Были найдены условия вычисления объёма тетраэдра.

Список используемых источников:

1. https://ru.wikipedia.org/wiki/%D4%EE%F0%EC%F3%EB%E0_%CF%E8%EA%E0 (дата посещения 12.11.2015)
2. http://hijos.ru/2011/09/14/formula-pika/ (дата посещения 13.11.2015)
3. http://matematikalegko.ru/formuli/ploshhad-figury-na-liste-v-kletku-formula-pika.html  (дата посещения 13.11.2015)
4. http://www.myshared.ru/slide/442221/ (дата посещения 20.11.2015)
5. http://e-maxx.ru/algo/pick_grid_theorem (дата посещения 13.11.2015)
6. http://www.mathschool.ru/storage/SCContent/555/%D0%94%D0%BE%D0%BA%D1%83%D0%BC%D0%B5%D0%BD%D1%82.pdf (дата посещения 14.11.2015)
7. http://kindlebook.ru/kursovaya-2/studentu/tvorcheskaia-rabota-primenenie-formuly-pika/ (дата посещения 12.11.2015)
8. http://hijos.ru/2011/12/30/georg-aleksandr-pik-1859-1942/ (дата посещения 22.11.2015)
9. http://library.kiwix.org/wikipedia_ru_all/A/html/%D0%A2/%D0%B5/%D1%82/%D1%80/%D0%A2%D0%B5%D1%82%D1%80%D0%B0%D1%8D%D0%B4%D1%80.html (дата посещения 22.11.2015)

 ГУЛЛИВЕР И ЛИЛИПУТЫ ПОМОГАЮТ ИЗУЧАТЬ МАТЕМАТИКУ

АВТОР ПРОЕКТА: Давлетшина Рената Владимировна,ученица 5 класса ГБОУ ЦО № 1296 г. Москва    

НАУЧНЫЙ РУКОВОДИТЕЛЬ: Майорова Елена Георгиевна, учитель математики ГБОУ ЦO № 1296 г. Москва

АКТУАЛЬНОСТЬ И ЗНАЧИМОСТЬ ПРОЕКТА: На основе сопоставления текстов художественных произведений, вычленения из них математических задач и их решения, поиска дополнительных данных, позволяющих сопоставить результаты с реальной жизнью, анкетирования и т.д. я пришла к выводу, что для учеников 4 - 5 классов получать новые знания по математике можно внимательно читая художественные произведения, авторы которых приводят интересные математические задачи. Математические знания могут пригодиться в самых разных, в том числе, необычных ситуациях, поэтому важно, чтобы школьникам как можно чаще предлагали нестандартные задачи, имеющие различные варианты решения, требующие определенной поисковой активности.

ЦЕЛЬ ПРОЕКТА: Проанализировав математические задачи из художественных произведений, а так же смоделированную Джонатаном Свифтом страну лилипутов и сопоставив ее (с помощью возможностей математики) с реальным миром, объяснить, почему ученики 4 - 5 классов, встречая в художественных произведениях математические задачи, редко их решают и доказать, что Гулливер и лилипуты могут помочь в изучении математики.

ЗАДАЧИ ПРОЕКТА:

• Выяснить основные трудности решения задач из произведений художественной литературы для школьников 4-5 классов.
• Определить все ли задачи из книги Джонатана Свифта «Гулливер в стране лилипутов» Я.И. Перельман включил в свой сборник «Веселые задачи» и если не все, то почему?
• Выяснить всегда ли Джонатан Свифт использует данные, соответствующие реальной действительности.
• Сформулировать задачи по книге Джонатана Свифта «Гулливер с стране лилипутов», которые можно было бы включить в учебник для V класса.

МЕТОДЫ ИССЛЕДОВАНИЯ: Работая над проектом я использовала следующие методы: анкетирование, анализ, моделирование, сравнительный метод, работу с различными источниками, обобщения.

ГИПОТЕЗА ИССЛЕДОВАНИЯ: Я предположила, что Джонатан Свифт, придумывая страну Лилипутию и ее жителей, не всегда точно соотносил ее пропорции с пропорциями реального мира. Задалась вопросом почему не все ситуации из жизни Гулливера в стране лилипутов использованы Я.И. Перельманом в его сборнике «Веселые задачи»?

ИТОГИ ИССЛЕДОВАНИЯ: Проведенное исследование позволило сделать следующие выводы:

1. В художественных произведениях часто встречаются очень простые задачи, которые решаешь устно и о которых забываешь, перевернув страницу.
2. Школьники не решают задачу самостоятельно, если автор прямо в тексте произведения подробно объясняет ее решение.
3. Математические задачи часто трудно вычленить из текста художественного произведения, так как они воспринимаются как описание кого-то или чего-то.
4. Решение математических задач требует владения дополнительной информацией. Например, знать, как соотнести различные меры длины, что такое водоизмещение, как принято было на Руси в XIX веке указывать рост человека.
5. Джонатан Свифт в книге «Путешествие Гулливера» приводит в основном правильные расчеты, хотя и допускает неточности и преувеличения. Причем всегда преувеличивает и никогда не преуменьшает результаты. Но в целом большинство результатов и ответов Джонатана Свифта согласовано с правилами математики.
6. Чем чаще в учебниках математики будут встречаться нестандартные задания, тем выше будет интерес учеников к математике.

СПИСОК ЛИТЕРАТУРЫ

1. Джонатан Свифт «Гулливер в стране лилипутов». Издательство: «Эксмо»,  2015
2. Н. Носов «Витя Малеев в школе и дома». Издательский дом: «Махаон», 2005
3. Л. Гераскин «В стране невыученных уроков», Издательство «Советская Россия» 1966.
4. Л.Н. Толстой «Арифметика», Москва, 1913.
5. Л.Н. Толстой «Азбука», Тула, 1995.
6. И. Тургенев «Муму». Издательство «Детская литература», 2015.
7. Я.И. Перельман «Веселые задачи» /http://xn--80aobchcjq2a.xn--p1ai/book-134/135

Автор: Горбушина Анастасия Дмитриевна, ученица 10 класса школы №5 п.Балезино Удмуртской Республики.

Руководитель: Касимов Рифхат Шамилович, учитель математики и физики школы№2 п.Балезино.

Проблема: современный подход к общему среднему образованию заставляет уделять особое место прикладным аспектам изучения математики. Среди задач математики , которые решают проблемы оптимизации, следует выделить задачи на экстремумы и оптимумы, с которыми в курсе математики средней школы приходится встречаться чаще всего. Эти задачи связаны с понятиями наибольшего, наилучшего, наиболее выгодного, в том числе и с понятием экстремума.

В школьном курсе математики они не изучаются. Однако эти задачи имеют большое практическое значение.С их помощью можно решить важный во всяком деле вопрос, как, по словам русского математика П.Л.Чебышева, "располагать средствами своими для достижения по возможности большей выгоды". Уметь решать подобные задачи очень важно, и поэтому они привлекают большое внимание математиков.

Предмет исследования: олимпиадная задача по математике.

Объект исследования: задача на оптимум в геометрии.

Цель иссследования: решить олимпадную задачу.

Задачи:

1.определиться с тематикой, планом и графиком выполнения работы;

2.подобрать и изучить литературу по теме исследования;

3.получить новые знания теоретического характера, ранее не известные мне;

4. построить чертежи различных видов треугольников и прямую, проходящую через вершину А треугольника, так, чтобы сумма  расстояний до неё от вершин В и С  была наибольшей;

5.собственная разработка олимпиадных задач, решаемых более эфективно через использование результатов моего исследования;

6.использовать практические результаты моего исследования для решения нестандартных олимпиадных задач.

Проведённое мною исследование позволит повысить интерес школьников к решению экстремальных задач.

Итог исследования: мне удалось полностью реализовать цели и задачи, поставленные передо мной моим руководителем, а также  сущностью и содержанием данной работы.Действительно, не только изучена дополнительная к школьному курсу литература, но и получены соответствующие теоретические сведения и практические результаты.

Литература:Возняк Г.М., Гусев В.А. Прикладные задачи на экстремумы.Москва, 1985

 Многие математические задачи допускают несколько вариантов решений. В этой работе рассматривается нестандартный способ решений различных алгебраических задач с помощью скалярного произведения векторов. Довольно большое число задач можно решить существенно проще по сравнению с решениями этих задач, выполненными традиционным путем, а в некоторых случаях, особенно, когда много переменных, только такой подход и приводит к успеху.

Научно-исследовательская работа по теме: «Сетевое моделирование как эффективный инструмент оптимизации организационной схемы производства»

Автор: Поспелов Леонид Игоревич, ученик 11 «А» класса МОУ-Гимназия №1 г. Клин

Научные руководители:

Дацко Елена Владимировна, учитель математики МОУ-Гимназия №1 г. Клин

Дацко Татьяна Геннадьевна, студентка 4-ого курса ФГБОУ ВО РЭУ им. Г.В. Плеханова

В последнее время теория графов стала одним из важнейших математических инструментов, которые широко используются в самых разнообразных областях науки и практики: составление расписаний и учебных планов, исследование структуры молекул, строительство и реконструкция предприятий, сегментация компьютерных программ и многое другое. Но, к сожалению, достаточно часто от людей разного уровня математической культуры и знаний можно услышать высказывания и суждения о теории графов, которые свидетельствуют о весьма поверхностной оценке возможностей и глубины этой теории.

Цель данной работы заключается в углублении и расширении теоретических знаний о сетевом моделировании, а также развитии практических навыков при самостоятельном построении ориентированного графа производственного процесса и расчете его параметров. Для достижения цели потребовалось выполнение задач:

1. Рассмотреть теоретические аспекты сетевого моделирования;
2. Произвести подробный расчет практического примера сетевой модели;
3. Представить план оптимизации производственного процесса.

Прежде всего, необходимо начать с терминологической базы исследования. Сетевым графом называется упорядоченная совокупность двух множеств – непустого множества вершин и множества двухэлементных пар вершин, называемых ребрами. Если на ребре указано направление, то его называют дугой. Если все соединения между вершинами графа изображаются с помощью дуг, то он называется ориентированным графом или сетевой моделью.

Помимо теоретических аспектов в данной работе автор рассмотрел практический пример применения сетевого моделирования при подготовке механического и сборочного цехов завода к массовому выпуску нового изделия. На полную реализацию задания было выделено 45 дней, а количество исполнителей не должно было превышать 17 человек.

Первым шагом являлось построение ориентированного графа, отражающего последовательность выполнения подготовительных работ. Следующий шаг заключался в расчете основных параметров событий орграфа – ранние и поздние сроки свершения t_р, t_п и резервы времени R. Рассчитанные параметры отражены на рисунке 1 в Приложении 2.

Определение цепочки работ, составляющих критический путь графа (A-D-E-H-I-J-N-P), позволило сделать вывод о том, что минимальное время, за которое производство может быть подготовлено к массовому выпуску нового изделия, составляет 43 дня, что подтверждает выполнимость поставленных временных целей (ограничений). Для наглядного представления плана работы основных подразделений завода был составлен специальный ленточный график – диаграмма Ганта .

В рамках аналитической части была проведена классификация работ сетевой модели по трудности их выполнения в установленные сроки. Для каждой работы был рассчитан коэффициент напряженности, соответственно которому были выделены три зоны: резервная, подкритическая и критическая.

Заключительный этап работы заключался в оптимизации организационной схемы производства, т.е. в корректировке и улучшении сетевого графика. Основываясь на исходных данных о численности трудовых ресурсов и ленточном графике разработки изделия, была построена диаграмма распределения числа работников по срокам выполнения работ . Из диаграммы следует, что в период с 6 по 13 дни и в 21 день количество работников превышает установленный исходными условиями задачи лимит 17 человек. Чтобы выровнять численность работников необходимо сдвинуть выполнение некритических работ. Оптимальным вариантом было выбрано сокращение сроков выполнения работ K и M, а также перенос работы L на период с 28 по 36 дни. Таким образом, сократив время на подготовку формальной документации на 2 дня и отсрочив начало подготовки оборудования цехов к контрольным испытаниям, удалось выровнять численность задействованных работников, не нарушая сроков окончания всего комплекса работ .

Обобщая изученную информацию, можно выделить ряд важных результатов практического применения орграфов:

• Четкая организационная увязка всех работ и участников моделируемого процесса;
• Выявление решающей цепочки работ от начала до конца разработки и сосредоточение внимания руководителей на этих работах;
• Возможность оперативной корректировки разработанных планов;
• Оптимизация затрат материальных, трудовых, финансовых ресурсов.

История теории графов – основы сетевого моделирования, насчитывает уже более двух столетий, однако, несмотря на наличие большого количества исследований и публикаций, эта область науки является недостаточно полно изученной и до сих пор остается в фокусе исследовательского интереса. Существует множество дискуссионных и слабо разработанных вопросов, которые формируют почву для дальнейшего изучения.

Список использованной литературы

1. Мир математики: в 40 т. Т. 11: Клауди Альсина. Карты метро и нейронные сети. Теория графов. / Пер. с исп. – М.: Де Агостини, 2014. – 144 с.
2. Новицкий Н.И. Сетевое планирование и управление производством: Учеб.-практ. пособие. – М.: Новое знание, 2004. – 159 с.
3. Организация и планирование машиностроительного производства. Учебник / Под ред. Ипатова М.И., Постникова В. И. и Захарова М.К. – М.: Высшая школа, 1988. – 367 с.

4. Уилсон Р.Дж. Введение в теорию графов. – М.: Издательство «Мир», 1977. – 208 с

Зуйкина Виолетта Николаевна, МКОУ Новоберезовская СОШ

Якунина Вера Владимировна, учитель математики, МКОУ Новоберезовская СОШ

Цель: Проследить как поэзия В.В. Маяковского может помочь запомноить старинные и новые единицы измерения.

Для объяснения связи новых мер со старыми Маяковский написал стихотворные тексты, которые печатались на конфетных обертках.

Старинные меры измерений были приблизительные. Мои измерения вершка, дюйма, пяди у пяти человек подтверждают это.

Социологический опрос учеников и родителей показал, что новое поколение не знает старинных мер измерения, происходит забывание своих национальных корней. Может, для того, чтобы этого не происходило стоит печатать на конфетных обертках стихи В.В. Маяковского.

Вывод: Поэзия В.В. Маяковского может помочь лучше понять и запомнить новые и старые единицы измерения и связь между ними.

ЛИТЕРАТУРА

1. М а я к о в с к и й  В.  В. Я сам. – М а я к о в с к и й  В.  В. Полное собрание сочинений в 13-ти томах. Т. 1. М., 1955, стр. 12.
2. Полном собрании сочинений, т. 4, ч. 2, М. 1936.
3. Владимир Маяковский. Полное собрание сочинений в тринадцати томах. Том пятый. Март-декабрь 1923. Реклама 1923-1925
4. Виленкин, Н.Я., Депман, И.Я. За страницами  учебника  математики [Текст]/ Н.Я. Виленкин, И.Я. Депман - М., 1981. – 217 с.
5. Детская энциклопедия «Нескучные числа» № 10-2012г.
6. Даль В.И. «Пословицы русского народа», М., «Астрель», 2008
7. Математический клуб «Кенгуру» «Книжка о дюймах, вершках и сантиметрах». Выпуск № 12-2011г.
8. Меры длины [Электронный ресурс]/ Режим доступа: http://www.iro.yar.ru, свободный. Загл с экрана. – Яз. рус.
9. История развития метрологии [Электронный ресурс]/ Режим доступа: http://www.metrologie.ru, свободный. Загл с экрана. – Яз. рус.
10. html//referat-doklad.ru  
11. rus-ved-rus.narod.ru/mery.html
12. http://www.shevkin.ru/?action=Page&ID=581

Автор исследования: Прасковьин Арсений Дмитриевич

Учебное заведение: МАОУ Самарский медико-технический лицей г.о. Самара, 6 класс.

Научный руководитель: Боякова Инна Александровна, учитель информатики МАОУ СМТЛ 

Тема исследования: Дизайнер интерьеров Floor Plan 3D: постройте дом своей мечты.

Актуальность исследования. С каменного века, когда люди переселились с деревьев в пещеры, человеку нужен был дом. И причём именно такой, какой он пердставляется в мечтах. Вам нравится дом в котором вы живёте? Если нет, так сделайте его лучше и удобнее, под себя! И пусть вам завидуют все соседи. Хорошей, белой завистью. В ноябре месяце 2014 года был проведён опрос в виде анкеты среди учеников 4-х классов и учителей лицея: "Дом вашей мечты?" В опросе приняло участие 39 человек. Из результатов опроса стало видно, что большинство участников хотят свой неповторимый дом. Любой дом начинается с проекта. Вот только как его, этот самый проект, разработать? В наше время услуги хорошего дизайнера стоят недёшево, да и вряд ли получится объяснить свой замысел так же чётко, как вы себе его продставляете. Но без знаний основ компьютерного моделирования, достаточно опыта, самому нарисовать весь проект тоже будет сложно. Таким образом опредилилась тема исследования.

Цель исследования: сформировать основы использования прикладного програмного обеспечения при создании проектов домов и иных объектов бытовой среды

Задачи исследования:

1. Познакомиться с программой FloorPlan 3D v6 и понятиями "архитектура", "интерьер", "дизайн"; 2. Научиться проектрировать здания и оформлять помещения по принципу "от простого к сложному"; 3. Использовать полученные знания и умения при самостоятельном творческом создании проектов; 4. Развивать навыки использования прикладного программного обеспечения при проектировании зданий.

Новизна исследования. На основе анализа имеющейся учебной и научной литературы сформирован не имеющий аналогов упрощенный алгоритм действий по освоению и использованию программы FloorPlan 3D v6., созданы обучающая презентация и электронная библиотека.

Содержание исследования. В работе решались задачи теоретической и практической направленности. Для раскрытия данной темы использовалась дополнительная литература и соответствующие интернет-источники, осуществлялся поиск и обработка необходимой информации. Благодаря печатной публикации и обучающей презентации на диске вы сможете познакомиться с такими понятиями как "архитектура", "интерьер", "дизайн" и узнаете, что русскоязычная программа российской компании "МедиаХауз" FloorPlan 3D v6. позволяет создавать собственный проект здания, используя только кнопики мыши, создавать уровни этажей, автоматически вставлять двери, окна, лестницы, колонны и крыши, снабжать вашу подель мебелью и предметами интерьера, создавать и распечатывать различные виды вашей модели, включая план и вид в 3D, т.е. объемный вид и многое другое.

Итоги исследования. Результатом самостоятельной творческой практической работы стало создание обучающей презентации и электронного приложения "Справочник проектов House-land" с большим разнообразием примеров и вариантов построек. Родители, учителя и учащиеся активно участвовали в обсуждении готовых проектов и вносили свои пожелания. Для более наглядного представления материала был создан рекламный буклет. 

Значимость исследования. Наша работа может быть полезна всем, кто впервые заниамется дизайном и перепланировкой жилых помещений и других сооружений, а также тем, кто сам участвует в постройке или переделке своего дома, квартиры или просто делает ремонт. Специалисты по ремонту, архитекторы, строители и просто учащиеся 3-11 классов могут использовать программу FloorPlan 3D v6. для быстрого создания эскизов и представления своих идей. Ведь чтобы работать с программой FloorPlan 3D, необходимо только уметь пользоваться мышью, выбирать параметры в меню, открывать и сохранять файлы.

Пусть придуманные нами дома не обязательно будут построены, но мы сможем уже сейчас внимательно рассмотреть их со всех сторон и изнутри, а также показать другим. Цель достигнута, но ещё много надо изучить в мире проектирования и дизайна. Главное - пробовать и не сдаваться! Экспериментируйте и набирайтесь опыта. Желаем удачи!

Список используемой литературы:

1. Браиловская Л.В. Дизайн квартир и реставрация мебели. - Ростов-на-Дону, Феникс, 2007;

2. Васечкина Д. Дизайн интерьера квартиры. Серия "Идеи для ремонта". - М.: Эксмо, 2005;

3. Владимировская А., Владимировский П. Дизайн уютного интерьера. - Ростов-на-Дону, Феникс, 2004.

4. Горячев А.В. Дизайнер интерьеров. - М.: БАЛАСС, 2007;

5. Горячев А.В. Мой инструмент компьютер. - М.:БАЛАСС, 2009;

6. Королев А.Л. Компьютерное моделирование/ А.Л. Королев. - М.: БИНОМ, ЛЗ, 2013;

7. Ларченко Д.А. Интерьер: дизайн и компьютерное моделирование/ Д.А. Ларченко, А.В. Келле. - СПб.: Питер, 2011;

8. Михеенкова О.В. Фасад дома. Оригинальный дизайн. - Ростов-на-Дону, Феникс, 2004;

9. Пташинский В.В. Проектируем интерьер сами Sweet home 3D, Floor Plan 3D, Google Sketch Up IKEA Home Planner. - СПб.: Питер, 2014;

10. Тарасевич Ю.Ю. Математическое и компьютерное моделирование. Вводный курс: Учебное пособие/ Ю.Ю. Тарасевич. - М.: ЛИБРОКОМ, 2013;

11. Технология. Учебник. Под ред. В.Д. Симоненко. - М.: Ветана-Граф, 2000;

12. Электронная энциклопедия "Ландшафтная архитектура". - М.: Студия Парус, 2005.

Разработка системы создания текстурных атласов

Автор: Медведев Егор Алексеевич.

Образовательное учреждение: Муниципальное общеобразовательное учреждение «Средняя школа с углубленным изучением отдельных предметов «Провинциальный колледж»

Научные руководители: Старший преподаватель кафедры сетевых и информационных технологий ЯрГУ им. П.Г. Демидова Легков Николай Васильевич;

Программист ООО «Tigrido Inc.» Бухарина Мария Александровна

Тезисы

Постановка задачи

Необходимо расположить изображения (прямоугольники) так, чтобы занимаемое ими пространство было минимальным при заданных ограничениях на область. Задача является NP-трудной, то есть не имеет «хорошего» по трудоемкости решения. В своей работе я постарался рассмотреть наиболее популярные и, насколько это возможно, эффективные алгоритмы. Задача является разновидностью задачи о двумерной упаковке рюкзака.

Цель работы

Разработать систему создания текстурных атласов для оптимизации хранения изображений в компьютерных играх.

Задачи

• Изучение способов хранения изображений для компьютерных игр.
• Разработка собственного приложения, позволяющего в интерактивном режиме создавать атласы из наборов изображений.
• Изучение возможности автоматизации процесса создания атласов.
• Реализация автоматизации создания атласов с использованием переборных алгоритмов и эвристик.
• Разработка рекомендаций по использованию приложения при создании компьютерных игр.

Алгоритмы решения

1) Next Fit.

Самый простой алгоритм. Совершает перебор «в лоб». Он действует следующим образом: из списка элементов выбирается самый высокий и устанавливается в левом нижнем углу целевого изображения, инициализируя текущий уровень. Далее, из оставшихся элементов выбираются элементы, не превосходящие по высоте и устанавливаются справа от него. Процесс продолжается до тех пор, пока есть свободное место на текущем уровне. Если на текущий уровень не помещается новый элемент, то элемент устанавливается выше и весь процесс начинается заново.

2) Best Fit. 

Алгоритм является модификацией предыдущего. От Next Fit он отличается тем, что перед установкой следующего прямоугольника для него ищется наиболее подходящее место (такое, что после его установки останется минимальное пространство).

3) Guillotine

Данный алгоритм отличается от двух предыдущих. Его суть заключается в следующем. Есть два списка: список с изображениями, подлежащими упаковке, и список прямоугольников, на которые упаковываются изображения из первого списка. В начальный момент времени в списке прямоугольников находится один большой – сам атлас. На него помещается первое изображение. Далее происходит деление прямоугольника пополам. Линия, разделяющая прямоугольник, проходит перпендикулярно большей стороне изображения. В итоге получается 2 прямоугольника, на которые устанавливаются последующие изображения из списка. Для них повторяется та же самая процедура. Алгоритм работает до тех пор, пока список изображений не пуст.

4) Maximal Rectangles

Идея данного алгоритма похожа на идею алгоритма Guillotine. Мы также разделяем прямоугольник на два, но при этом разделение происходит немного иначе: линии разделения проходят перпендикулярно обеим сторонам изображения и получаются два пересекающихся прямоугольника. Такая схема предоставляет нам большую свободу выбора наиболее подходящего прямоугольника для изображения. После упаковки мы просматриваем все прямоугольники в списке и вычитаем из них окаймляющий прямоугольник изображения. 

Итоги

• Исследованы различные алгоритмы решения задачи о двумерной упаковке рюкзака
• Спроектировано и реализовано приложение для создания текстурных атласов.

Список литературы

1. Jukka Jyänki. A Thousand Ways to Pack the Bin – A Practical Approach to Two-Dimensional Rectangle Bin Pack. // GitHub. – INTERNET: https://github.com/juj/RectangleBinPack/blob/master/RectangleBinPack.pdf
2. М. Шлее. Qt8. Профессиональное программирование на C++. – СПб.: БХВ-Петербург, 2013. – 912 с.
3. Г. Шилдт. Пер. с англ. Базовый курс C++. – М.: Издательский дом «Вильямс», 2014. – 624 c.
4. Про двумерную упаковку: offline алгоритмы. // Хабрахабр. – INTERNET: http://habrahabr.ru/post/136225/

ЗАДАЧА  О ПЛАВБАЗЕ

Автор: Шамкова Влада Сергеевна

Учебное заведение: МБОУ Мурманский политехнический лицей, 11 класс

Научные руководители: Бродский Исай Лазаревич, к.т.н., доцент. Место работы отсутствует (пенсионер)

Бережнов Сергей Геннадьевич, учитель высшей категории. Место работы: МБОУ г.Мурманска Лицей №4

Основной текст тезисов. Данная работа посвящена решению вопросов, поставленных Штейнгаузом в задаче «о школе для трех деревень».  Суть задачи заключается в следующем. Есть три деревни, в которых живут 50, 70 и 90 детей. Для этих деревень нужно построить школу так, чтобы суммарное время, затраченное на хождение всеми детьми в школу, было минимальным. Не меняя математического содержания задачи, мы видоизменили ее применительно к рыбопромысловой деятельности Мурманска. На трех банках ведут промысел траулеры в количестве 3, 4 и 6 единиц. Группу судов обслуживает плавбаза В, которой траулеры периодически сдают свою продукцию.

Цель. Наша цель - найти такое расположение плавбазы В, чтобы суммарное расстояние, пройденное всеми судами до плавбазы, было минимальным. Дать ответы на воспросы, поставленные Штейнгаузом в его задаче.

Штейнгауз предлагает путь решения данной задачи. На стол положить карту местности и пробуравить отверстия там, где располагаются рыболовные банки. Пропустить через отверстия нити, верхние концы которых связаны в узелок, а к нижним концам привязаны нагрузки в 3, 4 и  6 условных единиц. Узелок должен показать оптимальное расположение плавбазы для этих трех банок.

Вопросы Штейнгауза:

1) Почему узелок дает нужное решение?

2) Как найти положение узелка геометрически?

3) При каких условиях узелок совпадет с положением одной из деревень?

Актуальность. Совершенствование экономико-математических методов промысловой деятельности связано с реальной экономией соответствующих материальных средств, что определяет актуальность исследования.

Новизна работы заключается в том, что поставлены и решены дополнительные задачи, не содержащиеся в постановке Штейнгауза. В частности решен вопрос об аналитическом способе нахождения искомой точки. Впервые показана связь задачи Штейнгауза с некоторыми вопросами экономики промысловой деятельности Мурманска.

Итоги исследования 

1. В работе рассмотрена задача Штейнгауза об оптимальном расположении плавбазы, обслуживающей траулеры на трех банках (у Штейнгауза эта задача сформулирована для оптимального расположения школы, обслуживающей три деревни).

2. Дано обоснование механической интерпретации задачи и ее решения с помощью грузиков.

3. Дана геометрическая интерпретация задачи и ее решения.

4. В дополнение к вопросам Штейнгауза поставлен и решен вопрос об аналитическом расчете координат оптимального расположения плавбазы.

5. Найдено условие инвариантности оптимального положения плавбазы относительно перемещений точек   и  - банок промысла групп судов.

6. Найдено необходимое условие для оптимальной постановки плавбазы на одной из банок.

7. Выполнен демонстрационный прибор в виде настольной карты с отверстиями, соответствующими положениям промысловых банок, и грузиками, связанными ниткой так, что узелок показывает искомое положение плавбазы.

 Литература

1. Гуго Штейнгауз "Математический калейдоскоп", гостехиздат, М-Л.:  1949, стр.47

2. Выгодский М.Я. "Справочник по высшей математике", наука, М.:1967

3. Тарг С.М. "Краткий курс теоретической механики", наука, М.:1967

4. Демидович Б.П, Марон И.А."Основы вычислительной математики", наука,М:1996

Название: ПУТЕШЕСТВИЕ ВОКРУГ СВЕТА ЗА 80 ДНЕЙ В 19 ВЕКЕ : ПРАВДА ИЛИ РЕАЛЬНОСТЬ.
ФИО автора: Селиванова Дарья Сергеевна, ученица 5 класса
ГБОУ ЦО №1296 г. Москва
ФИО руководителя: Майорова Елена Георгиевна, учитель математики, ГБОУ ЦО № 1296 г. Москва
Цель работы: пройти путем Филеаса Фогга вокруг света за 80 дней, проанализировать художественно смоделированной Жюль Верном  реальности.
Задачи:
изучить произведение Жюль Верна «Вокруг света за восемьдесят дней»;
начертить карту, проложить маршрут;
определить расстояния между основными пунктами путешествия;
уточнить виды транспорта и узнать их скорости во времена Жюль Верна;
предоставить отчет о путешествии, доказав, что Филеас Фогг мог (или не мог) совершить кругосветное путешествие за 80 дней;
узнать, кто сумел побить рекорд Филеаса Фогга в то время, когда была написана книга;
определить условия, при которых Филеас Фогг не выиграл бы пари;
определить, сколько времени затратили бы на это путешествие сейчас, пользуясь современными видами транспорта; пользуясь теми же видами транспорта.
Методы исследования:
1.общенаучный (теоретический);
2.практический;
3.технологический (ИКТ).
Актуальность данной работы: работа индивидуальна, интересна, были изучены новые темы по математике,  хотелось бы проектом повысить интерес к изучению математике, показав применение математических знаний в необычной обстановке, занимательных примеров применения математических знаний, тем самым привлекая детей к изучению математике и повышая их интерес к этой науке.
Данная работа важна тем, что наглядно показывает, что математика – это не просто школьный предмет, а наука, находящая применение в жизни.
Практическое применение работы состоит в том, чтобы использовать  знания и умения в решении задач по математике, расширении кругозора учащихся.
Итоги исследования: был проложен маршрут Филеаса Фогга, определены расстояния между пунктами путешествия, сумели узнать, кто побил рекорд Филеаса Фогга в то время, когда была написана книга, определены условия, при которых Филеас Фогг не выиграл бы пари, а также рассчитано, сколько времени затратили бы на это путешествие сейчас, пользуясь современными видами транспорта; пользуясь теми же видами транспорта.
Список литературы:

1. Жюль Верн. Вокруг света за 80 дней. Издательство « Детская литература», Москва,1979г.
2. http://timecalc.ru
3. Википедия.
4. Детская энциклопедия. Земля. Издательство «Педагогика», Москва,1971г.

Манцурова Ольга Вячеславовна,

МОУ Лицей №1 г.Волгограда.

Научный руководитель: Шмадченко Евгения Александровна,

учитель математики МОУ Лицей №1.

МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ И МИНИМУМЫ НА ПЛОСКОСТИ

Предмет исследования: поверхности мыльных пленок в опытах Плато и минимальная сумма отрезков, соединяющих точки плоскости.

Цель исследования: выяснить, существует ли взаимосвязь  между минимальными поверхностями и минимумами на плоскости.

Задачи исследования:

1. Изучить проблему Плато и провести некоторые опыты Плато.
2. Найти минимальную сумму отрезков, соединяющих вершины треугольника и квадрата.
3. Выяснить, какое применение минимумов на плоскости может найти человек для своей деятельности.

Методы исследования: эмпирическое описание, эксперимент, выдвижение гипотезы, доказательство утверждений.

Гипотеза:  кратчайшая система отрезков, соединяющих вершины треугольника и квадрата аналогична расположению линий натяжения мыльных пленок на контурах куба и тетраэдра, которые ортогонально спроецированы на одну из граней данных многогранников.  

Результатами работы стали расчёт потенциальных затрат при проектировании экономичной сети автодорог, соединяющей четыре населенных пункта; моделирование оптимизированного подземного перехода; определение экономически выгодного расположения склада для хранения товаров, предназначенных для доставки в магазины. Это и определило актуальность нашего исследования.

Библиографический список 

1.Полатоз, М.С. От мыльной пены к технологическим достижениям

/ М.С. Полатоз // Новые грани. – 2009. – № 18. – С. 34 – 39.

2.Фоменко, А.Т. Минимальные поверхности  / А.Т. Фоменко // Квант. - 1983. – № 6. – С. 18 – 20.

3.Коксетер, Г. С. М. Новые встречи с геометрией / Г. С. М. Коксетер, С. Л. Грейтцер— М.: Наука, 1978. – 224 c.

4.Тихомиров, В. М. Рассказы о максимумах и минимумах/ В. М.Тихомиров —2-е изд. исп. — М.: МЦМНО, 2006. — 200 с.

5. Болтянский, В. Г. Геометрические задачи на максимум и минимум. /В. Г.Болтянский, И.М.Яглом. Энциклопедия элементарной математики: кн. 5. — М.: Наука, 1966. — с. 270—348.

Название научно-исследовательской работы: «Кристаллы»
Автор работы: ученица 9 класса Хаярова Рузиля Рустамовна, обучающаяся в Республике Башкортостан МБОУ СОШ с.Прогресс Янаульского района.
Научный руководитель: Давлетханова Лидия Накыйповна, учитель физики МБОУ СОШ с.Прогресс
Цель исследования:
- узнать историю кристаллов;
- исследовать области применения кристаллов;
- вырастить кристаллы в домашних условиях и провести наблюдение за их ростом.
Кристалл - это твердое тело природного происхождения, либо образованное в лабораторных условиях, имеющее форму правильного многогранника. Правильность формы кристалла основана на его внутренней структуре-частицы вещества, из которых слагается кристалл, располагаются в нем в определенной закономерности и образуют периодично-повторяющуюся трехмерную пространственную укладку, иначе называемую «кристаллической решеткой».
Кристаллы образуются и на стенах пещер, на скалах, и в сырых ущельях. Существуют даже кристаллы, которые можно съесть! Это соль и сахар, которые имеются на каждой кухне. Кристаллы широко применяются в науке и в технике.

Актуальность: данная тема является актуальной в связи с тем, что выращивание кристаллов очень интересное и увлекательное занятие. Я очень люблю узнавать все новое и интересное, мне нравится экспериментировать, наблюдать и собирать коллекции.

Итоги исследования: выращивать кристаллы можно не только в химических и промышленных лабораториях, но и в домашних условиях. Самые популярные вещества, из которых выращивают кристаллы дома – это поваренная соль, морская соль, сахар и медный купорос. Выращенные кристаллы небольшой формы можно использовать в качестве украшения, например, рамки для фотографий или других предметов. Проведя данную исследовательскую работу, можно утверждать, что выдвинутая гипотеза, подтвердилась. Кристалл можно вырастить в домашних условиях, но для этого нужно изучить процесс их формирования. Я уверена, что приобретенные мной знания, умения и навыки обязательно пригодятся в дальнейшей учёбе.
Изучение данной темы вызвало у меня большой интерес, и я хочу продолжить свою работу над изучением кристаллов. В моих планах в дальнейшем вырастить кристаллы из сахара и соды.

Список использованной литературы:
⦁ Александр Китайгородский «Кристаллы»
⦁ Степан Вартанов «Мир кристаллов»
⦁ Шубникова «Образование кристаллов»
⦁ http://fismat.ru/fis/glava6/11.htm
http⦁ ://⦁ ru⦁ .⦁ wikipedia⦁ .⦁ org
http⦁ ://⦁ www⦁ .⦁ bibliofond⦁ .⦁ ru⦁ /⦁ view⦁ .⦁ aspx⦁ ?⦁ id⦁ =661295
⦁ http://about-crystall.ru/vyrashhivanie-kristallov-iz-povarennoj-soli/

                                                     Прогрессии рядом с нами

Работу выполнила: Буклина Анастасия Сергеевна, 8 класс
Научный руководитель: Шошкина Вера Васильевна,учитель математики
Учреждение: МБОУ СОШ № 12 имени В.В.Тарасова

Цель работы: узнать применение формул арифметической и геометрической прогрессии при решении задач и подготовиться к сдаче ЕГЭ, научившись решать задания с прогрессиями.
Актуальность: ЕГЭ - это единый государственный экзамен, система экзаменов, которые в обязательном порядке сдают все выпускники 11 классов всех типов школ. Выбирать для сдачи в форме ЕГЭ можно любой предмет из школьной программы, но обязательными предметами являются все те же, что и на ГИА: русский и математика. После сдачи ЕГЭ ученик получает сертификат с баллами, который он может использовать при поступлении в любой вуз на территории России.Чем лучше результаты ЕГЭ,тем больше шансов для поступления в желаемый вуз.
Проблема , изложенная в моем проекте, заключается в том, что для успешной сдачи ЕГЭ требуется умение решать задачи на последовательности и прогрессии. Но в курсе средней школы эта тема изучается только в 9 классе и немного в 10. По моему мнению, в процессе изучения материала недостаточное внимание уделяется задачам повышенной трудности, умение решать которые –необходимое условие для качественной подготовки к ЕГЭ.
Задачи:
1. Подобрать и изучить литературу по данной теме.
2. Прорешать задачи из сборника задач по подготовке к ЕГЭ 2016, используя формулы арифметической и геометрической прогрессий.
3. Создать электронную презентацию работы для представления собранного материала старшеклассникам.
4. Сравнить и проанализировать результаты исследования.
5. Сделать вывод.
Объект исследования: арифметическая и геометрическая прогрессия и их свойства.
Предмет исследования: применение формул прогрессий при решении задач ЕГЭ и их практическая значимость.
База исследования: МБОУ СОШ №12 г. Пенза имени В.В. Тарасова
Заключение: В нашей жизни многое очевидно с помощью математики, в частности, арифметической и геометрической прогрессий. Я рассмотрела несколько сфер деятельности человека и убедились в том, что применение математики в жизни может избежать многих проблем.А так же мы провели исследование и выяснили,что ученики 9 и 8 классов усвоили материал практически на одном уровне. Я считаю ,что изучение данной темы можно начинать в 8 классе. Это позволит в 9 и 11 классах больше времени уделить к общей подготовке к ОГЭ и ЕГЭ

В связи с ростом использования компьютерных технологий люди сталипереходить на электронные книги, учебники. В мире множество людей, которые хотели бы создать свое учебное пособие или книгу. И сделать это проще, чем кажется.

Цель проекта: создание электронной книги.

Задачи проекта:

1. Освоить возможности программ MS PowerPoint и iSpring Suite.

2. Ознакомиться с технологией создания электронной книги.

3. Создание книги с помощью различных программ.

Здесь будет описанно выведение формул нахождения - синуса, косинуса, тангенса, котангенса через комплексные числа, выведение формулы натурального логарифма комплексного числа и формулы возведения комплексного числа в степень.

В книге [1] поставлена такая задача: исследовать количество корней уравнения  в зависимости от a, b, c; изобразить соответствующие области в пространстве параметров  (a, b, c). Цель нашей работы – привести уравнение четвертой степени к виду, содержащему два коэффициента, и изобразить на плоскости этих коэффициентов области, в которых уравнение имеет данное количество действительных корней.

Вывод: уравнение четвертой степени заменой неизвестной приведено к одному из трех видов:

x⁴=px+q;

x⁴+x²=px+q;

x⁴-x²=px+q; для каждого из них на плоскости (p, q) указаны области, где уравнение имеет данное количество решений. Поставленная цель достигнута.

Использованная литература

1. Сгибнев А.И. Исследовательские задачи для начинающих. – М.: МЦНМО, 2013.

Наше время-период невиданного расцвета математики.На наших глазах происходит новая техническая и информационная революци.Ничто в нашей жизни невозможно без математики ,в том числе и физика. В своей работе я рассмотрю отношение математики к физикеи докажу ,то что физика невозможна без математики.Я рассмотрю арифметическую и геометрическую последовательности,узнаю ,что такое метод Гауса и решу несколько физических задач с помощью математических методов.

Цель: разработать алгоритм сортировки массивов, который будет превосходить изученные алгоритмы на определённом типе элементов или в общем случае.

Задачи:  

изучить и проанализировать  основные алгоритмы сортировки массивов;

разработав новый алгоритм, – поразрядная сортировка подсчётом – доказать экспериментальным путем, что он является одним из самых быстрых на массивах с большим количеством элементов и самым экономным по памяти среди самых быстрых алгоритмов.

Краткое описание работы: были изучены алгоритмы: сортировка выбором, пузырьковая сортировка, гномья сортировка, быстрая сортировка, сортировка слиянием. Было протестировано время работы с помощью тестовой системы VisualStudio 2015. Дополнительные затраты памяти были рассчитаны теоретически, на практике проверялось лишь отношение (больше или меньше памяти затрачено). Был создан собственный алгоритм, названный поразрядная сортировка подсчётом.

Актуальность и новизна исследования: в современном мире количество упорядочиваемой информации увеличивается очень быстро, и если бы алгоритмы сортировки не развивались вместе с ними, такие упорядочивания происходили бы очень медленно. Поэтому одновременно с ростом количества информации нуждаются в развитии и алгоритмы сортировки.

1. Прикладной проект на тему: «Робот для автоматизированного сбора картографической и метеорологической информации в пешеходных, парковых зонах городов»;
2. ФИО автора работы: Стасьев Денис Олегович;
3. Образовательное учреждение, в котором обучается автор работы: МБОУ «Гимназия №7 имени Героя России С.В. Василёва» г. Брянска;
4. ФИО, должность и место работы научного руководителя: Степаниденко Александр Иванович, учитель физики МБОУ «Гимназия №7 имени Героя России С.В. Василёва» г. Брянска;
5. Цель проекта: создать робота, предназначенного для автоматизированного сбора картографической и метеорологической информации в пешеходных, парковых зонах городов, внутри протяженных промышленных помещений и сельскохозяйственных сооружений.

Задачи:

1. изучить необходимую информацию по данной теме;
2. описать общее устройство системы;
3. определить устройство аппаратной части робота;
4. создать и распечатать 3D-модели деталей системы на 3D-принтере;
5. настроить аппаратную часть робота;
6. написать скетч (программу) для модели в среде разработки Arduino (IDE);
7. провести тестирование робота.

Работа посвящена разработке и созданию робота, предназначенного для автоматизированного сбора картографической и метеорологической информации в пешеходных, парковых зонах городов, внутри протяженных промышленных помещений и сельскохозяйственных сооружений. В проекте представлен путь возможного решения проблем, связанных с неточностью информации, представленной в существующих картах и в метеорологических прогнозах. В настоящее время существуют автоматизированные комплексы, входящие в составы картографических информационно-поисковых систем, которые способны самостоятельно собирать информацию о различных параметрах исследуемой территории. В масштабах городов подобные установки крепятся на автомобилях, которые не подходят для использования в пешеходных зонах. Продукт проекта сможет автоматизировано собирать данные о пешеходных, парковых зонах городов, отслеживать параметры температуры, влажности и атмосферного давления в архивах и на предприятиях с особым режимом работы, а также увеличит детализацию информации. В работе описывается устройство системы, процесс создания аппаратной и программной частей робота, последняя из которых основана на частично бионическом алгоритме, который был заимствован у живых существ. В ходе работы над проектом были созданы и распечатаны на 3D-принтере в научно-промышленной компании «Интеграция» города Брянска 3D-модели некоторых крепёжных деталей. Разработана программа для дистанционного управления роботом по Bluetooth-соединению. Проведено тестирование системы.

Проекта является актуальным и значимым, так как он решает ряд проблем. Во-первых, решает проблему плохой детализации пешеходных, парковых зон городов. Позволяет увеличить производительность труда людей при сборе данных, необходимых для составления карт.  Во-вторых, решает проблему неточностей в метеорологических прогнозах, связанных с сильной удалённостью метеостанций от текущего местоположения пользователя. В-третьих, продукт проекта может быть использован для контроля определённых условий.

Созданный робот может быть использован в составе информационно-поисковых систем, которые способны самостоятельно собирать информацию о различных параметрах исследуемой территории. Комплекс таких роботов сможет автоматизировано собирать и контролировать параметры окружающей среды пешеходных, парковых зон городов, на предприятиях с особым режимом производства, за счёт чего решит поставленные проблемы.

От родителей, старших друзей мы давно слышали о теореме Пифагора. И вот в 8 классе мы ее изучили. Учитель нам рассказала о важности теоремы, о некоторых исторических фактах. И мы решили рассмотреть этот вопрос более подробно. Цель нашей работы: выявить, насколько широко используется теорема Пифагора в математике и в нашей жизни. В своей работе мы рассмотрели личность Пифагора, историю теоремы, привели несколько доказательств теремы Пифагора, выявили, в каких областях применяется теорема, решили задания из КИМов ОГЭ. Мы думаем, что наш проект пригодится на уроках, элективных занятиях, внеурочной деятельности, внеклассных мероприятиях по математике, физике, черчению, классных часах.

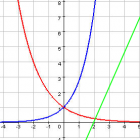
Построение произвольных графиков функций, моделирование функций методом наименьших квадратов.

Лапин Дмитрий Игоревич

Россия, Липецкая область, Липецк, МБОУ СОШ №14

Научный руководитель:      Шуваева Елена Александровна, учитель физики в МБОУ СОШ №14

В жизни люди не редко сталкиваются с графиками функций.  Ведь график наглядно показывает нам как зависит одна координата от другой. Это помогает визуализировать информацию. С помощью графика очень удобно смотреть статистику, мониторить информацию, решать некоторые математические задачи, решать другие подобные задачи.

Таким образом, выбранная тема является достаточно актуальной и перспективной.

 Целью данной работы стало моделирование самих функций из набора точек и непосредственно построение графиков этих или произвольных функций.

 Задачи работы: подготовка динамической  системы координат, расчёт значений зависимой координаты от основной, построение графика функций, моделирование функций из набора точек с помощью метода наименьших квадратов.
Особенности системы

1. Построение одновременно до 3-х графиков.
2. Возможность изменения масштаба и расположения осей координат.
3. Моделирование нескольких графиков функций МНК по заданному набору данных.
4. Возможность автоматической или ручной сортировки функций выведенных методом МНК.
5. Сохранение промежуточных результатов работы.
6. Возможность вывода на печать или сохранения изображения с графиками.

Области применения

Данная система полезна для изучения различных функций, метода наименьших квадратов, построения наглядных зависимостей нескольких величин от одного значения.

Данная система полезна для моделирования функции зависимости Y = f(X) из большого количества экспериментальных данных, т.е. вместо большого количества конкретных данных можно хранить только одну зависимость.

Также возможно использование отдельных модулей этой программы (построение графиков, математический калькулятор, нахождение функции МНК) в других областях, системах, так как эти модули не привязаны друг к другу.

Список литературы

1. Линник Ю. В. "Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений". — 2-е изд. — М., 1962.
2. Емельянов В.И. Воробьев В.И., Тюрина Т.П. "Основы программирования на Delphi".

1. Тема: « Геометрия в лесу и у реки»;
2. Маркина Екатерина Дмитриевна, Шабалина Ольга Павловна;
3. Муниципальное бюджетное нетиповое общеобразовательное учреждение «Городской классический лицей» (далее – МБНОУ «ГКЛ»); 
4. Андриянова Татьяна Васильевна, учитель математики, МБНОУ «ГКЛ»;

Цель: Проведение измерительных работ на местности, применение законов геометрии на практике. Задачи:1.Рассмотреть способы определения высоты предмета и расстояния до недоступной точки. 2.Рассмотреть способы определения скорости течения реки.3.Показать нестандартные пути использования  геометрических знаний в повседневной жизни. 4. Составить  и решить геометрические задачи.

1. Гипотеза: Можно ли определить расстояние до недоступного предмета на местности, скорость течения реки без специальных приборов. Методы: теоретический: анализ литературных и учебных источников; эмпирический: анализ и сравнение полученных результатов. Практическая значимость: геометрия – это не просто школьный предмет, а наука, находящая применение в повседневной жизни человека.

Глава 1. Ключевые подходы к определению расстояния до недоступной точки

1.1. Измерение пирамиды по способу Фалес

Фалес заключил, что его собственная тень равна его росту, когда солнечные лучи встречают ровную почву под углом в половину прямого, и вершина пирамиды, центр ее основания и конец ее тени должны обозначать равнобедренный треугольник.

1.2.  Измерение высоты дерева с помощью глазомера

В результате проведенных 10 измерений на «глаз» было установлено, что высота дерева равна 9,8 м. Измерение проводили с помощью  сравнения единичного отрезка и наложение отрезков на длину предмета. X = (8+11+12+9+9+10+11+9+10+9):10 = 9,8 м

1.3.  Измерение высоты дерева с помощью тени

Задача: Длина тени от человека равна 453 см, а длина тени дерева – 2697 см. Найдите высоту дерева, если рост человека составляет 160 см.

Вывод: 952,6 см. Высота дерева во столько же раз больше роста человека, во сколько раз тень дерева больше тени человека. Использовали первый признак подобия треугольников.

1.4.  Измерение высоты дерева в случае его наклона к горизонту

Задача: Длина тени дерева (АК) , растущего под наклоном,  равна 2697 см. На высоте один метр от земли повесили кепку(В), которая дает тень.  Длина тени от основания дерева до тени от кепки (АС), равна 306 см. Длина от кепки до земли (ВН) составляет два метра. Найдите угол В; высоту дерева.

Вывод: высота дерева равна 974 см. Решение через подобие ∆ и теорему синусов.

1.5.  Измерение высоты дерева с помощью зеркала

Задача: Расстояние от ствола дерева до зеркала составило 674 см, а от зеркала до человека – 259 см. Найдите высоту дерева, если рост человека равен 160 см.

Вывод: высота - 416 см. Два треугольника с соответственно равными углами являются подобным, и отношения их соответственных сторон равны.

1.6.  Измерение расстояния до объекта с помощью спички

Задача: Высота фонарного столба равна 210 см, а длина – 6 см. Найти расстояние от глаз человека до объекта, если между спичкой и человеком, смотрящим на нее, 60 см.

Вывод: Самым доступным способом мы считаем измерение  расстояния до объекта с помощью спички. Расстояние от глаз человека до фонарного столба составляет 21 метр.

Глава 2. Определение скорости течения реки

2.1.  Измерение скорости течения реки на расстоянии 4-х метров от берега

Задача: Первый пятиметровый отрезок пути поплавок проплыл за 4,68 секунд, а второй – за 5,09 секунд. Вычисли среднюю скорость течения реки.

Вывод: V_ср= ;  V_ср=1,02 м/с≈4 км/ч

2.2.  Измерение скорости течения реки на расстоянии 8-ми метров от берега

Задача: Первый пятиметровой отрезок пути поплавок проплыл за 3,71 секунды, а второй – за 3,54 секунды. Вычислите среднюю скорость течения реки.

Вывод: V_ср= ; V_ср=1,4 м/с≈5 км/ч. Скорость течения реки около берега замедляется, а к середине реки увеличивается.

Заключение: В ходе работы мы применяли  различные способы измерения расстояний до недоступных точек, средней скорости реки. Все способы показались простыми и удобными, т.к. заняли мало времени, минимум приспособлений для решения задач.

1. На летней практике, проходившей в 2015 году под девизом: «Отдых + Математика = Собственный учебник задач», которая была на территории базы отдыха «Алтан» в Горном Алтае, мы учились применять теоретические знания по геометрии на практике.
2. Использование приборов, механизмов и приспособлений в наше время значительно упрощает жизнь современных людей. Но иногда возникают чрезвычайные ситуации, когда нет возможности применить технические средства.
3. Высоту предмета, расстояние до недоступной точки на местности можно определить «на глаз» или используя тень от предмета, рулетку, зеркало, спичку, зная первый признак подобия треугольника и теорему синусов. Скорость течения реки в походных условиях измеряется с помощью поплавка и секундомера. Задачи составлены самостоятельно и решены с использованием геометрических знаний в окружающем нас мире.

Приложение

1.2.  Измерение высоты дерева с помощью глазомера

Таблица1

1.3.  Измерение высоты дерева с помощью тени

∆АВС~∆А₁В₁С₁

1.4.  Измерение высоты дерева в случае его наклона к горизонту

1.5.  Измерение высоты дерева с помощью зеркала

∆ABC=∆A₁BC ; ∆A₁BC ~ ∆EDC

1.6.  Измерение расстояния до объекта с помощью спички

∆АDE ~ ∆АВС

2.1.  Измерение скорости течения реки на расстоянии 4-х метров от берега

2.2.  Измерение скорости течения реки на расстоянии 8-ми метров от берега

Литература:

1. Л. С. Атанасян и др. Геометрия: учебник для 7-9 кл. общеобразовательных учреждений. – М.: Просвещение, 2013.
2. Ф.Б. Брохгауз. Иллюстрированный энциклопедический словарь. М. Эксмо, 2006-960с.
3. Я.И. Перельман. Занимательная алгебра, занимательная геометрия. М. АСТ, 2007-267с.
4. Я.И. Перельман. Занимательная геометрия. М. АСТ, 2005-138с.
5. О.И. Юрченко. Методы мотивации и стимулирования деятельности учащихся. Математика в школе, №1, 2005
6. http://www.scouts.ru «Центральный сайт скаутов-разведчиков России»

Научно-исследовательская работа

«Применение математики в авиа-моделировании и авиастроении»

Россия, Забайкальский Край, город Чита
Автор

Скороход Максим Сергеевич
МБОУ «Многопрофильная гимназия№12 г.Читы»
5 «В» класс

                                                                                                              Научный руководитель

                                                                                                      Рогалева Елена Николаевна

                                                                                                                 Учитель математики

                                                                                                               Научный консультант

                                                                                                   Сущенко Руслан Алексеевич

                                                                                    Педагог дополнительного образования

                                                                                        Областной станции юных техников

                                                                                      Преподаватель авиа -моделирования

Цель работы

Выявление результатов применения математических методов в построении модели самолета.

Задачи

• Изучить литературу по областям : математика, геометрия, история авиации.
• Выяснить где и как применяется математика в авиа-моделирование и авиастроении.
• Показать результат моего исследования.
• Доказать что математика связана с авиа-моделированием и авиастроением.

Методы и приёмы, которые использовались в работе

1. Теоретический метод
   1. Изучение ранее опубликованной литературы
   2. Анализ
   3. Научное моделирование
2. Эмпирический метод
   1. Измерение
   2. Сравнение
   3. Материальное моделирование

Причины использования предлагаемых методов и приёмов

• простота
• наглядность
• точность

Полученные данные

Наглядное представление кордовой гоночной модели самолета F2C

Вывод

В ходе проведения научной-исследовательской  работы было доказано, что  современное авиастроение основано на математических методах.

               План исследований

Проблема
Какова взаимосвязь между математикой, авиа-моделированием и авиацией.

Актуальность проблемы  и практическое использование результатов.

Кордовая гоночная модель самолета F2C выступает как математический объект. Объединяются знания по математике, геометрии, авиа-моделированию, физики. И реализация их на практике.

Объект  исследования

Кордовая гоночная модель самолета F2C.

Предмет исследования
Понятия и законы математики, физики в авиа-моделировании.   

Гипотеза

 Если предположить, что авиастроение основывается на математических методах, то можно выявить, какие математические методы лежат в основе моделирования.

Описание метода. Этапы поведения исследования

1. Выбор темы, формулировка проблемы.
2. Изучение теоретического материала по авиа-моделированию, авиастроению, математики.
3. Поиск ранее проведенных исследований на данную тему.
4. Выбор объектов исследования (кордовая гоночная модель самолета F2C) и методов решения проблемы.
5. Создание модели.
6. Проведение анализа объекта, проверка гипотезы.
7. Сбор, систематизация полученных материалов, оценка результатов.
8. Написание самой работы.

Компонентно-ориентированная технология разработки кроссплатформенных приложений

Крютченко Федот Игоревич

Школа Программиста, ЦДО «Хоста» г. Сочи, 9 класс

Научный руководитель: Лазарев Михаил Юрьевич

Цели:

1) Изучить методики разработки web-приложений

2) Описать технологию разработки серверной и клиентской частей приложений

3) Выполнить апробацию технологии примере разработки конкретной клиент-серверной многопользовательской программы

Задачи:

1) Исследовать применение библиотеки Google Polymer на примере создания web-приложения.

2) Описать и реализовать удаленный вызов процедур (RPC) на базе протокола HTTP.

3) Исследовать особенности использования RPC на клиентской и серверной части программы.

4) Продемонстрировать разработанные технологии на примере конкретной реализации.

5) Дать оценку полученному результату.

В рамках данной работы автор описывает разработанную им технологию, позволяющую создавать кроссплатформенные приложения. Согласно разработанной автором технологии, для создания web-приложения разработчику необходимо выполнить следующие действия.

Для разработки серверной части:

1) Определить список ролей пользователей (например, администратор системы, модератор, автор, контроллер, кассир и т.д.)

2) Описать список функций, которые будут вызываться удаленно, эти функции соответствуют операциям, производимым соответствующими пользователями в системе;

3) Опубликовать соответствующие функции путем размещения их в подготовленной

автором структуре данных и распределить права на вызовы отдельных функций между ролями.

Для разработки клиентской части:

1) Для каждой роли создать компоненту, отвечающую за экран, которую при входе в систему видит пользователь каждой из ролей.

2) Для каждой созданной компоненты-экрана создать необходимые компоненты, отвечающие за функции данного экрана, путем разбиения этого экрана на составляющие.

3) Разработчик продолжает разбиение компонент до тех пор, пока разбиение не дойдет до элементарных компонент. При этом компоненты, разработанные для использования в рамках одной роли пользователей, повторно используются для создания рабочих мест (экранов) для других ролей.

Актуальность:

Существует большая потребность в создании кроссплатформенных web-приложений, которые организуют работу или другое взаимодействие больших человеческих коллективов. Для создания таких приложений требуется устойчивая и проверенная технология, то есть набор инструкций, следуя которым можно с разумными трудозатратами получить приложение, дальнейшее сопровождение и разработка которого не будет создавать проблем.

Значимость:

Данная технология, по мнению автора, будет востребована среди программистов, разработчиков комплексных систем управления, которым необходимо держать сложность проектов под контролем.

Новизна:

Несмотря на то, что кроссплатформенные приложения существуют давно, способ разработки кроссплатформенных приложений на основе web-технологий появился недавно.

Итоги:

Разработана и описана компонентно-ориентированная технология разработки кроссплатформенных приложений. В рамках этой работы созданы библиотеки, которые на сервере реализуют удаленный вызов процедур на базе протокола HTTP. Также разработана библиотека web-компонент, в рамках которой на клиентской части реализуется удаленный вызов серверных процедур.

Создано web-приложение, на котором апробировано использование разработанной технологии.

Метод оценки схожести текстов на основе евклидовой метрики в многомерном пространстве

ЮСИФОВ Эльнур Сеймурович

Школа программиста, ЦДО «Хоста», 9 класс

Научный руководитель: ЛАЗАРЕВ Михаил Юрьевич

Цели исследования

1. Разработать математический метод анализа и оценки схожести текстов, т.е. определения расстояния между ними.

2. Реализовать данный метод в виде программы и исследовать возможности данного метода.

3. Предложить на основе данного метода технологии, позволяющие осуществлять поиск текстов, выдачу рекомендаций для читателя по интересующим его темам, автоматическую группировку и классификацию текстов по их тематике.

Задачи исследования

1. Выполнить автоматизированную подготовку корпуса текстов, на котором будут осуществляться эксперименты.

2. Сформулировать основные положения метода классификации текстов.

3. Разработать комплекс программ, реализующих метод классификации текстов.

4. Оценить результаты экспериментов, предложить серию усовершенствований метода, реализовать их.

5. Разработать программы, реализующие выдачу рекомендаций для читателя по заданному тексту, а также поиск текстов по ключевым фразам.

6. Оценить полученный метод в целом и указать на дальнейшие направления его развития.

Автор разработал программу, которая позволила ему собрать достаточный для проведения исследования корпус текстов. С помощью этой программы с научно-популярного сайта «Хабрахабр» было автоматически скачано около 20 000 статей, а затем проведена их обработка и выделение из них текста. Далее автор разработал программу, с помощью которой было выполнено преобразование полученных текстов в вектора. Идея преобразования состоит в следующем: (1) взять все уникальные слова изо всех текстов, и пронумеровать их, и (2) преобразовать все тексты в вектора, где i-я компонента вектора соответствует количеству вхождений i-го слова в текст. Получив множество таких векторов, мы можем находить между парами векторов расстояния и сравнивать их, трактуя эти величины как показатели «похожести» или «различия» текстов. В этом состоит суть метода, исследуемого автором.

В ходе исследования на основе данного метода была разработана компьютерная программа, с помощью которой были получены экспериментальные данные о евклидовом расстоянии между различными текстами корпуса. На их основе автор сделал выводы о том, что данный метод можно усовершенствовать в следующих направлениях: (1) использовать вместо слов их основы, (2) нормировать векторы, (3) не принимать в расчет часто встречающиеся, а также уникальные слова. Эти усовершенствования также были реализованы, и автор приводит экспериментальные результаты, подтверждающие, что качество поиска значительно улучшилось.

Актуальность исследования

В настоящее время стремительно растёт объем информации, к которой человек может получить доступ. В этом потоке становится все сложнее находить полезную, интересующую человека информацию. Необходимо создание и развитие автоматизированных систем, классифицирующих и отбирающих информацию. Автор в данной работе ищет подходы к решению этой проблемы, актуальность которой на сегодняшний день велика, и в будущем, вероятно, будет только возрастать.

Значимость и новизна исследования

В рамках данного исследования автор демонстрирует, как на базе простой идеи получить эффективный алгоритм оценки схожести текстов. На его основе предлагается осуществлять поиск текстов, выдачу рекомендаций для читателя по интересующим его темам, автоматическую группировку и классификацию текстов по тематике. Данный метод можно применять в различных сферах, включая работу информационных агентств, библиотек научно-технической информации, научных и образовательных учреждений.

Итоги исследования

В ходе исследования автор решил поставленные задачи и получил метод, позволяющий эффективно оценивать схожесть текстов. Автор планирует продолжить исследование метода, в частности, реализовать в будущем автоматическое определение множества слов, значимых для оценки текста.

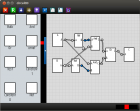
Программа проктирования и моделирования логических схем

Терляхин Даниил Романович

Школа программиста, ЦДО «Хоста» г.Сочи, 8 класс

Научный руководитель: Лазарев Михаил Юрьевич

Цели иследования

1) Изучение принципов работы логических элементов и их схем
2) Создание программы, моделирующей работу логических элементов
3) Усовершенствование программы возможностью объедения элементов в схемы
4) Реализация возможностей сохранения логических схем и использования их как элементов в других схемах

Задачи иследования

1) Выбрать язык программирования и графической библиотеки
2) Реализовать логическую модель элемента
3) Разработать компоненты для графического пользовательского интерфейса программы
4) Реализовать графический пользовательский интерфейс
5) Дать оценку полученному результату и определить планы для дальнейшего исследования

Описание работы

В данном проекте автор задался проблемой создания программы проектирования логических схем, а также их моделирования. То есть в данной программе пользователь может не только собрать логическую схему, но и увидеть, как данная логическая схема функционирует.

Автор изучил теоретическую часть основанную на булевой алгебре и провел анализ программ-аналогов.

Для разработки программы использовался язык программирования Python. Автор начал с создания логической части программы и разработал алгоритм работы логических схем на основе двух моделей: контакта и примитивного элемента. Это позволило на уровне языка программирования собирать логические схемы и моделировать их работу. Важной особенностью является также и то, что логическую схему можно определить как элемент и в дальнейшем использовать в составе более крупной логической схемы.

Далее перед автором встал вопрос графического редактирования логических схем. В качестве графической библиотеки автор решил выбрать низкоуровневую библиотеку Pygame. Данная библиотека предоставляет возможность работы с графическими примитивами низкого уровня. Поэтому автор самостоятельно разработал на ее базе такие компоненты, как: кнопки, вкладки, панели, строка состояния, перетаскиваемые объекты, диалоги и поля ввода.

Актуальность работы

Проектирование логических схем является актуальной темой, поскольку главные детали современных ЭВМ состоят из логических элементов. Работу логических схем необходимо моделировать для того, чтобы избежать ошибок в работе компьютеров, которые будут собранны по этим схемам. Поскольку выпуск микропроцессора обходится в миллионы долларов, очень важно сконструировать виртуальную логическую схему и проверить ее работоспособность и возможности еще до того, как она будет отправлена в производство. 

Значимость исследования

Работа логических схем изучается в рамках булевой алгебры. Таким образом, разработанная автором программа может также использоваться как интерактивное учебное пособие.

Также данную программу могут использовать инженеры для проектирования сложных логических схем.

Итоги исследования

Автор разработал программу, позволяющую проектировать и моделировать логические схемы.

На основе этой программы автор выполнил исследования работы логических схем, включая вопрос о том, как можно собрать реализацию любой логической функции из небольшого набора базовых элементов. В настоящее время программу, разработанную автором можно использовать в качестве учебного пособия. В будущем автор планирует продолжить работу над программой и сконструировать с помощью этой программы логическую модель микропроцессора.

О НЕКОТОРЫХ СПОСОБАХ ПРИМЕНЕНИЯ МЕТОДА МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ В ТЕОРИИ ЧИСЕЛ ФИБОНАЧЧИ

Дичина Регина Павловна (Нижегородская область, г. Саров, МБОУ Лицей № 3, 10 класс)

Руководитель: Столяров Игорь Васильевич, учитель математики и информатики,

МБОУ Лицей № 3

Цель:

В данной работе рассматриваются особенности применения метода математической индукции при доказательстве ряда теорем в теории чисел Фибоначчи.

Актуальность исследования:
          Метод математической индукции является одним из самих универсальных методов доказательства математических утверждений [1,2], и он применяется в задачах на доказательства равенств, неравенств и задачах на делимость и суммирование [3].

Значимость и новизна:
         Новизна данного исследования заключается в том, что при доказательстве данных теорем был использован множественный подход с разбиением на подмножества и многократное использование метода математической индукции, что существенным образом отличается от существующих способов применения метода математической индукции [1-3].

           Краткое описание научно-исследовательской работы:
       С применением метода математической индукции на основании рекуррентных соотношений, связывающих каждые три соседних числа Фибоначчи и симметричные гиперболические функции Фибоначчи в данной работе были доказаны следующие теоремы.

Теорема 1. Все числа ряда Фибоначчи лежат в проекции Золотого Шофара на плоскости XOY.

Для доказательства теоремы 1 все множество чисел Фибоначчи было разбито на четыре подмножества: четные числа Фибоначчи (симметричный синус Фибоначчи sFs(x)), нечетные числа Фибоначчи (симметричный косинус Фибоначчи cFs(x)), четные расширенные и нечетные расширенные числа Фибоначчи в сторону отрицательных значений индекса n. Для каждого из множеств по методу математической индукции (с переходом к натуральному индексу) на основании рекуррентных соотношений были доказаны соответствующие равенства, связывающие каждые три соседних числа Фибоначчи.

Теорема 2. Трехмерная спираль Фибоначчи лежит на Золотом Шофаре, в плоскости XOY она проецируется в квази-синусоидальную функцию Фибоначчи и пересекает плоскость XOY в точках, которые соответствуют числам Фибоначчи.

Особенности применения метода математической индукции при доказательстве теоремы 2 заключаются в том, что для комплексного представления трехмерной спирали Фибоначчи были отдельно доказаны соответствующие соотношения для действительной и мнимой части.

Развитие нового («непрерывного») подхода к «Теории чисел Фибоначчи» [4-6] состоит в том, что она является вырожденным, «дискретным» случаем «теории гиперболических функций Фибоначчи и Люка», а любому «непрерывному» тождеству для гиперболических функций Фибоначчи и Люка соответствует некоторое «дискретное» тождество для чисел Фибоначчи и Люка и наоборот [7-9].

Вывод:
В данной работе были рассмотрены особенности применения метода математической индукции при доказательстве ряда теорем в теории чисел Фибоначчи.

Литература

1. Ивнин А.А. М. Логика. М.: Фаир-Пресс, 2002.
2. Математический форум MathHelpPlanet. Обсуждение и решение задач по математике, физике, химии, экономике - http://mathhelpplanet.com/
3. Шарыгин И. Ф. Факультативный курс по математике: Решение задач// Учебное пособие для 10 кл. средней школы. М.: Просвещение, 1989. - 252с.
4. Гладкова Л. О проекциях Золотого Шофара . XIV Школьные Харитоновские чтения. Межрегиональная олимпиада школьников «Будущие исследователи – будущее науки». Тезисы. Саров: ФГУП  «РФЯЦ-ВНИИЭФ», 2014,  с.7-8.
5. Stakhov A., Rozin B.The Golden Shofar // Chaos, Solitons & Fractals, 2005, Volume 26, Issue 3, p. 677-684.
6. Stakhov A., Rozin B. On a new class of hyperbolic function // Chaos, Solitons & Fractals, 2004, Volume 23, Issue 2, p. 379-389.
7. Стахов А.П. Гиперболические функции Фибоначчи и Люка: история и приложения // «Академия Тринитаризма», М., Эл № 77-6567, публ.14429, 31.05.2007 (trinitas.ru/rus/doc/0232/009a/02321057.htm)
8. Stakhov A.P.Hyperbolic Fibonacci and Lucas Functions: A New Mathematics for the Living Nature. — Vinnitsa: ITI, 2003. – 240 с.

       Игра "Полоска" состоит в следующем: в полоске, состоящей из нескольких клеток, два игрока по очереди закрашивают либо одну, либо две соседние клетки (соседние клетки - клетки, имеющие общую сторону). Красить клетки повторно нельзя. Выигрывает тот, кто закрасит последнюю клетку.

       Цель работы: найти выигрышную стратегию в игре "Полоска".

       В работе проанализированы случаи полосок разной длины, начиная с простейших (3 клетки), и заканчивая полосками в N клеток, где N - любое целое число. Задача была усложнена рассмотрением случаев, когда полоска замкнута в кольцо, а также анализом подобной игры на игровом поле - прямоугольнике.

       Итогом исследования являются найденные для каждого рассмотренного случая выигрышные стратегии.

"Геометрическое доказательство алгебраических неравенств о средних величинах"

Радайкина Елена Анатольевна

МОУ "Лицей №31",11 класс

Певцова Ольга Викторовна, учитель математики и геометрии , МОУ "Лицей №31"

 Цель исследования: геометрическое доказательство алгебраических неравенств о средних величинах и применению этих доказательств при  решении различных геометрических задач. 

Задачи:

1) сбор информации из различных источниках о приемах и методах доказательств неравенств

2) рассмотреть алгебраическое и геометрическое доказательство теорем о средних величинах

3) ознакомиться с применением неравенств в других областях математики

 Сейчас в школьных учебниках используется алгеброическое доказательство, хотя геометрическое доказательство более наглядно и проще.

 В первой главе моей работы "Числовые средние в античности" рассматривается история возникновения средних величин в математике и первое доказательство неравенств о средних в Древней Греции.

 Во второй главе "Числовые средние и геометрия" рассматривается обобщение средних величин на n чисел и приводится алгеброическое доказательство неравенства о среднем арифметическом и среднем геометрическом.

 В главе "Алгебраическое и геометрическое доказательства теорем о средних величинах.

 В четвертой главе, которая называется "Применение неравенств с числовыми средними" приводятся различные способы применения этих неравенств в других областях математики.

 В главе пятой собраны задачи, которые решаются с использованием торем о средних величинах.

 Неравенства для средних и сами средние широко применяются не только в алгебре, геометрии, математическом анализе, но и в статистике,в теории вероятностей, при обработке результатов измерений.

 Неравенства играют фундаментальную роль в большинстве разделов современной математики, без них не может обойтись ни физика, ни астрономия, ни химия. Теория вероятности,     математическая статистика, экономика - все эти взаимосвяханные и обобщающие друг друга науки  постоянно используют неравенства.

Вывод:

Еще с древних времен было известно несколько способов построения средних по двум данным отрезкам a и b.

 Доказательства неравенств помогают развить навык осмысления и применения приемов доказательства неравенств; умение применять их при выполнении различных задач; умение анализировать, обощать и делать выводы; логически излагать мысли; творчески относиться к делу.  

Список литературы:

1)Детская энцеклопедия, том 2. Второе издание. Издательство Просвещение Москва 1965г.

2)Прасолов В.В. Сборник задач по планометрии Ч.II-М.:Наука.

Гл. ред. физ.-мат. лит., 1989-(Б-ка мат. кружка).-288 с.

3)Журнал "Квант" 1971г. №2 стр. 20-22

4)Журнал "Квант" 1979г. №4 стр. 61-64

5)Журнал "Квант" 1980г. №3 стр. 22-23

6)Журна "Квант" 1986г. №2 стр. 17

7)Энциклопедический словарь юного математика. Сост. Э. 68

А.П. Савин.-М.:Педогогика, 1985 г.-352с.,ил.   

Все вы слышали о такой головоломке, как кубик Рубика. Наверняка каждый из вас пробовал собрать такой кубик. Мы решили исследовать эту головоломку: есть ли закономерность в сборке кубика Рубика, как собрать его за минимальное и простое количество этапов. В этом исследовании мы подробно всё вам объясним.

Игра «Лабиринт»

Цель: разработка игры «Лабиринт», проектирование и создание игрового движка, проектирование и разработка модели взаимодействия игрока с объектами в игровом мире, проектирование и реализация алгоритмов генерации случайного игрового мира.

Актуальность: тема работы была выбрана по нескольким причинам:

1) Компьютерное моделирование позволяет более детально изучить процессы, происходящие в природе, за счёт перехода на определённый уровень абстракции.

2) Алгоритмы генерации случайного игрового мира являются интересным для исследования направлением, в котором существует достаточный простор для изучения и создания новых алгоритмов, доработки существующих алгоритмов.

Описание методов: в своем проекте я использовал интегрированную среду разработки CodeBlocks на языке С++. Программа адаптирована под выполнение и протестирована в операционных системах Microsoft Windows XP/7/8.1/10 (x86/x64). В приложении реализована техника наложения графических текстур на физические модели объектов (для решения этой задачи применены возможности графической 2D-библиотеки). Мною были спроектированы и реализованы алгоритмы генерации случайного игрового мира. Данные алгоритмы были разработаны путём создания случайного двухмерного массива с последующей его корректировкой набором условных конструкций. В программе реализовано управление персонажем пользователя с использованием клавиатуры в качестве устройства ввода. Реализовано взаимодействие персонажа пользователя с объектами игрового мира (различные препятствия, различные по типу виды ландшафта – деревья, песок, вода и т.д.) на основе алгоритма определения коллизий. В данном алгоритме задействован метод проверки 8-и значимых пикселей.

Анализ: в процессе выполнения проекта была разработана игра «Лабиринт», в которой мне удалось реализовать физические модели и их взаимодействие с окружающим иговым миром. Мной был придуман метод 8-ми пикселей, с помощью которого можно добиться ощутимого ускорения в работе программы. Игровой мир при каждом запуске приложения уникален, формируется случайным образом алгоритмами генерации случайного мира и составляет около 1000 на 1000 визуальных объектов. В каждый момент игры пользователь видит только 40 объектов на экране, покрытых текстурами, остальные объекты скрыты. Реализован плавный переход между видимой и скрытыми областями на основе разработанного мной алгоритма. Данный алгоритм можно будет применять при разработке секционной модели игрового мира и формировании обзорной карты игрового мира.

Автор: Волосова Анжелика Георгиевна

Образовательное учреждение: МАОУ "Лицей №37" г. Саратова

Руководитель: Гущина Ирина Николаевна, учитель математики МАОУ "Лицея №37"

Логика - наука старая. Она возникла, когда развитие специальных наук и вообще человеческого мышления сделало актуальным вопрос о том, как надо рассуждать, чтобы получить правильные выводы. Интерес клогике впервые возник среди математиков и философов эпохи расцвета греческой культуры в 6-4 вв. до н.э. 

Математическая логика отличается от "обычной" тем, что она широко пользуется языком математических и логических знаков. Начало математической логики, положенное Аристотелем еще в далеком 4 вв. до н. э., и позднее Джордж Буль, превративший математическую логику в алгебру высказываний, дали огромный толчок для развития вычислительных машин в современном мире...

Целью моей работы является знаккомство с алгеброй высказываний:

- научиться решать задачи с помощью алгебры высказываний;        

- научиться вычислять значения истинности сложных высказываний;          

- найти практическое применение алгебры высказываний.

В итоге этой работы я научилась применять алгебру высказываний в решении задач. также я поняла принцип работы алгебры высказываний в электрической цепи и вычислительных машинах.

Список литературы:                                      

В.Е.Шевченко "Некоторые способы решения логических задач" 1979 г.;    

И.Я.Депман "Первое знакомство с математической логикой" 1963 г.;

А.Н.Колмогоров, А.Г.Драгалин "Математическая логика. Введение в математическую логику" 2013 г.;

С.И.Шапиро "Кибернетика" 1984 г.;          

Л.М.Лихтарников, Т.Г.Сукачева "Математическая логика" 1999 г.

Исследователький проект "Математика в кристаллах"

автор проекта: Малкина Ольга Евгеньевна учащаяся 5 Б¹ класса МАОУ «СОШ № 33 с УИОП

руководитель проекта: Лобанова Татьяна Владимировна методист Центра работы с одаренными детьми КГОАУ «Центр образования «Эврика», г.Петропавловск-Камчатский

Цель исследования – изучить природные кристаллы с математической точки зрения.

Объектом  исследования стали кристаллы веществ.

Для достижения цели исследования были поставлены следующие задачи:

1. Изучение литературы.
2. Подготовка материала для исследования.
3. Исследование.
4. Систематизация данных исследования.

Основной метод исследования – эксперимент. Предметом исследования является выявлением математических элементов в кристаллах.

Проектным продуктом являются выращенные методом перекристаллизации монокристаллы.

Практическая значимость исследования заключается в том, что проведенное исследование и его результаты могут стать началом дальнейшего изучения кристаллов и их структур с математической, химической и физической точек зрения.

В школьном курсе математики мы познакомились с различными геометрическими телами. В ходе изучения предмета «Окружающий мир», изучили понятие кристалла. Кристалл – это твердое состояние вещества. Он имеет определенную форму и определенное количество граней вследствие строго закономерного расположения своих атомов. Все кристаллы одного вещества имеют одинаковую форму, хотя и могут отличаться размерами. Среди геометрических тел есть многогранники, которые имеют грани. Тот факт, что кристаллы имеют определенное количество граней, меня заинтересовал. Эти размышления были положены в основу моего исследования,цель которого, изучить природные кристаллы с математической точки зрения.

Методы исследования, которые использовались в исследовательской работе: наблюдение, фотографирование, измерение, сравнение, эксперимент, лабораторный опыт, моделирование, изучение и обобщение.

Для проведения исследования были изучены методы выращивания кристаллов. Для выращивания кристалла был выбран медный купорос, потому что его кристалл растет довольно быстро.

Для того, чтобы его вырастить использовался метод осаждения из насыщенного раствора. Монокристалл медного купороса кристаллизуется из водных растворов сульфата меди и представляет собой ярко-синие кристаллы. После того как кристалл медного купороса был выращен, он был высушен и покрыт лаком. Обрисовав все грани кристалла, была построена его модель из бумаги. При помощи транспортира были измерены все углы. Значения углов на выращенном кристалле совпали с теоретическими сведениями из изученной литературы и составили соответственно 97,5, 94 и 125 градусов. Тем самым, экспериментальным путем был получен тот факт, что в кристаллах одного вещества углы между соответственными гранями всегда одинаковы, то есть выполняется закон постоянства углов. У кристаллов медного купороса имеется лишь центр симметрии, других элементов симметрии у них нет.

Процесс выращивания кристалла оказался увлекательным занятием. И электролитическим методом был также выращен поликристалл меди, а методом осаждения из насыщенного раствора поликристалл ортофосфата аммония.

Таким образом, экспериментальным путем было получено, что кристаллы обладают математическими элементами. Все они являются многогранниками, обладают свойствами симметрии, для них выполняется закон постоянства углов. Работая над проектом, я научилась выращивать кристаллы, делать развертку многогранников, научилась строить сечения многогранников. Практическая значимостьисследования состоит в том, что проведенное исследование и его результаты могут стать началом дальнейшего изучения кристаллов и их структур с химической и физической точек зрения.

Научно-исследовательская работа: Фракталы.Исследование и моделирование.

Автор работы: Григорьева Анна Олеговна

11 класс

Образовательное учереждение: Муниципальное автономное образовательное учереждение гимназия №1 г.Белебей.

Научный руководитель:

Смоленцева Вера Николаевна, учитель информатики в гимназии №1 г.Белебей.

Цели и задачи:

Целью научно-исследовательской работы является изучение такого, столь молодого и быстроразвивающегося направления математики, как фрактальная геометрия.

Одной из главных задач является изучить фракталы в целом:историю,виды и применение, а также более глубоко исследовать способы моделирования некоторых фракталов и постараться смоделировать их на школьном языке PascalABC.

Актуальность:

Актуальность прежде всего обусловлена тем, что фрактальная геометрия находит сейчас все больше и больше различных применений в науке и жизни человека, так как по сути все наше мироздание один большой фрактал. И изучение и систематизирование информации о них-одна из важнейших задач.

Описание научно-исследовательской работы:

В работе произведено исследование фракталов:появление,история,виды и применение. Также проведена работа для более глубоко изучения способов построения некоторых фракталов и написаны программы на языке PascalABC для визуального представления каждого из них. 

Значимость и новизна исследования:

Полученные программы могут являются примером того, что несмотря на то, что объект с виду может казаться сложным и невозможным для построения в несколько простых действий(а тем более на обычных школьных компьютерах и в таком простом языке школьного программирования как Pascal),на самом деле обычно достаточно прост,стоит только рассмотреть его поближе.

Итоги исследования:

В результате исследования была рассмотрена и систематизирована инфромация о фракталах и разных его видах. Также были изучены способы построения несколький знаменитых фракталов и написаны программы для их построения.

Список использованной литературы:

1. Божокин С.В., Паршин Д.А. Фракталы и мультифракталы.

2. Мандельброт Б. Фрактальная геометрия природы.

3.Морозов А.Д. Введение в теорию фракталов.

На основе принципа электромоделирования транспортных потоков мною разработана моделирующая программа,  позволяющаюя рассчитать  и визуализировать  характеристики участка магистрали.

Основная часть моей научно-исследовательской работы содержит рассмотрение и одно из множества доказательство теоремы Пифагора и решение задач на эту тему, а так же рассмотрение свойств Пифагоровых троек, нахождение и использование алгоритма их вычисления, непосредственную проверку алгоритма для любых натуральных чисел с заданными условиями.

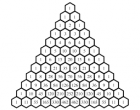
1. Треугольник Паскаля

2. Семичук Артём Сергеевич

3. МАОУ "Лицей №37" г. Саратов

4. Гущина И.Н. учитель математики и информатики МАОУ "Лицей №37" г. Саратов

5. Цель проекта

- ознакомиться с треугольником Паскаля;

- рассмотреть применение треугольника Паскаля в различных сферах; 

Задачи

- изучить литературу по теме «Треугольник Паскаля»;

- выявить свойства чисел, входящих в состав треугольника Паскаля;

- научиться строить треугольники Паскаля;

- определить применение свойств чисел треугольника Паскаля;

- сформулировать вывод и итоги исследования;

6. Предмет исследования:  свойства треугольника Паскаля

Методы исследования:

- аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;

- поиск информации в интернет - ресурсах.

7. Актуальность

Данный проект предназначен для выявления того, как треугольник  Паскаля можно использовать в жизни.

8.Новизна проекта

Новизна исследования состоит в том, чтобы  показать связь арифметических треугольников с разными задачами.

Практическая значимость проекта

Данный проект может быть использован как дополнительный материал к урокам математики.

9. Заключение

Вывод - одной из наиболее известных и изящных численных схем во всей математике является треугольник Паскаля.

10.Список использованных источников и литературы

1. Абачиев С. К. Радужная фрактальность треугольника Паскаля
2. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля // Математические новеллы. — М.: Мир, 1974. — 456 с. 3. Треугольник Паскаля. В. А. Успенский. - 2 - е изд. – М.: Наука, 1979. – 48с.
3. Удивительный треугольник великого француза // Hard'n'Soft № 10 2003
4. Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17-25.
5. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. – М.: Аванта+,2004. – 688с.
6. Weisstein, Eric W. Pascal's Triangle (англ.) насайте Wolfram MathWorld.
7. Паскаля треугольник // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 230-232. — 352 с.
8. Фукс Д., Фукс М.Арифметика биномиальных коэффициентов  // Квант. — 1970. — № 6. — С. 17-25.
9. Энциклопедический словарь юного математика, 1985
10. О. В. КузьминТреугольник и пирамида Паскаля: свойства и обобщения
11. // Соросовский Образовательный Журнал. — 2000. — Т. 6, № 5. — С. 101—109.
12. Удивительный треугольник великого француза //Hard'n'Soft. — 2003. — № 10.
13. Weisstein, Eric W.Pascal's Triangle (англ.) на сайте Wolfram MathWorld.
14. Мартин Гарднер.Глава 17. Неисчерпаемое очарование треугольника Паскаля // Математические новеллы. — М.: Мир, 1974. — 456 с.
15. http://inf.1september.ru/2002/1/france.htm
16. http://schools.techno.ru/sch444/MUSEUM/PRES/PL-4-98.htm

С раннего детства я занимаюсь танцами. Со временем я стала понимать, что танец- это не только красивые движения ппод музыку, но и множество математических формул связанных в одно целое. В своей работе я постараюсь это доказать.

ЗАДАЧА ШТЕЙНЕРА

Шангареев Антон Нургалеевич, 9 класс,

МБОУ г. Иркутска Лицей №1.

Научный руководитель: Мельникова Мария Ивановна,

Учитель математики высшей квалификационной категории МБОУ г. Иркутска Лицея № 1.

Задача Штейнера — это задача о соединении заданного набора точек некоторой сетью так, чтобы длина этой сети была минимальной. При этом можно использовать дополнительные точки. Эта задача имеет полное решение, но, поскольку она относится к классу NP-полных, для задачи Штейнера не существует алгоритма, позволяющего получить решение за полиномиальное время.

Гипотеза:

Существуют алгоритмы приближенного решения задачи Штейнера, работающие за полиномиальное время.

Цель:

Построить оптимальный алгоритм, работающий за минимальное время и позволяющий построить сеть минимальной длины (среди аналогичных алгоритмов).

Для достижения цели были поставлены следующие задачи:

1. Проанализировать учебную литературу по данной теме.
2. Решить задачу Штейнера для трёх точек.
3. Определить свойства сетей Штейнера и построить алгоритм решения задачи для любого количества точек.
4. Рассмотреть различные алгоритмы построения приближенный решений задачи.
5. Составить компьютерную программу на C++/Qt для построения решений с помощью выбранных алгоритмов.
6. Обобщить свои наблюдения и сделать выводы по итогам работы.

Ход работы:

При выполнении работы были рассмотрены следующие алгоритмы приближенного решения задачи, позволяющие за полиномиальное время получить достаточно короткую сеть:

• Алгоритм Крускала.

Этот алгоритм выполняет построение минимального остовного дерева (без дополнительных точек). Известно, что сумма длин ребер такого дерева не более, чем в  раз превышает длину минимальной сети Штейнера. Это утверждение называется гипотезой Гильберта-Поллака, и недавно она была доказана.

• Алгоритм, основанный на гравитационной модели и триангуляции Делоне.

В отличие от алгоритма Крускала, в алгоритме на основе гравитационной модели используются дополнительные точки. Однако получившаяся сеть обычно не является сетью Штейнера, так как углы между ребрами дополнительных вершин лишь приблизительно равны 120 градусам.

Итог работы:

Были выполнены поставленные задачи: рассмотрено несколько алгоритмов построения приближенного решения задачи Штейнера. Была написана компьютерная программа на C++ для построения приближённых решений с использованием данных алгоритмов.

Актуальность:

В изначальном виде задача Штейнера относится к классу NP-полных задач. Если для нее будет найдено полиномиальное решение, либо будет доказана невозможность получения такого решения, это будет эквивалентно решению «проблемы равенства классов P и NP», которая является одной из «Задач тысячелетия».

Приближённые решения, а также различные варианты задачи используются для минимизации длины телекоммуникационных сетей, проектирования электронных схем и в некоторых других областях в прикладной роли.

Список литературы:

Эвристический алгоритм поиска приближенного решения задачи Штейнера, основанный на физический аналогиях, научная статья, Лисин А.В., Файзуллин Р.Т.

Steiner Minimal Trees / E.N. Gilbert, H.O. Pollak Journal on Applied Mathematics. – 1968. – Vol. 16.

Триангуляция Делоне и её применение / А.В. Скворцов. – Томск: Издательство Томского университета, 2002.

Цель научной работы: определить свойства функции, показывающей зависимость количества взвешиваний и числа объектов взвешивания. Методы: поиск, анализ решений и ответов на задачи, конспектирование, реферирование, количественный анализ результатов, анализ литературы, классификация задач, решений и ответов по типам, метод сравнительно-сопоставительного анализа, описательный метод, оценочный метод. Основные результаты научного исследования: была обобщена известная задача про взвешивание определенного числа объектов, произведено сравнение с уже имеющимися решениями задачи общего случая и выявлено, что представленное нами решение имеет ряд преимуществ. Также был построен график и определены свойства функции, выведенной при решении задачи с обобщённым условием.

В моей работе идёт речь от парадоксе Бертрана. Парадокс Бертрана заключается в следующем: рассмотрим равносторонний треугольник, вписанный в окружность. Произвольно выбирается хорда окружности. Какова вероятность того, что выбранная хорда длиннее стороны треугольника? Бертран предложил три решения, очевидно верных, но дающих различный результат. Однако инструментами высшей математики можно показать, что вероятность определяется единиственным образом. Кроме того, мною проведён эксперимент, он показал те же результаты, что были получены теоретически.

1. Название научно-исследовательской работы: Invis

2. Автор: Михайлов Александр Алексеевич, учащийся 11А класса многопрофильной гимназии №12 г.Твери

Соавторы:

Остимчук Ярослав Иванович, учащийся 10Б класса

гимназии №6 г. Твери

Волдохин Денис Михайлович, учащийся 11А класса

многопрофильной гимназии № 12 г.Твери

4.Научный руководитель: Учитель высшей категории Харинова Галина Вячеславовна

5.1 Проблема: В наше время многие испытывают нужду в использовании контента "вконтакте". Главной проблемой является то, что для этого нужно входить в свой аккаунт.

5.2 Цель работы:  показать людям то, что времяпровождение в социальной сети может быть абсолютно анонимным. Я создал приложение, которое позволяет использовать бы все функции "вконтакте", минуя процесс авторизации.

6. Основная часть: Приложение представляет собой клиент-серверное приложение. Сервер подгружает посты к себе в базу данных, и через определённый промежуток времени обновляет информацию о них. Таким же образом подгружаются аудиозаписи, видиозаписи, а также картинки. Когда клиент подключается к серверу, начинается обмен сообщеними. Протакол разработан мной и сообщения передаются в виде json документов. На сервере стоит обработчик, который в зависимости от запроса клиенты, вызывает определённый метод. Если пользователь делает запрос на получение контента, который не находится в постоянном обновлении, то этот контент подгружается с "вконтакте", записывается в базу данных и передаётся клиенту.

Сервер написан на языке java, использовались такие техналогии, как google gson, hibernate.

 7. Актуальность: Представьте себе знаменитую личность, сотни людей следят за её страницей. Один только выход в сеть данной персоны на каком-нибудь мироприятии вызовит социальный взрыв. Наше приложение позволяет получить контент соц сети абсолютно анонимно, так как всю работу клиента берёт на себя сервер.

8. Новизна: Подобных проектов не существует, а проблема становится актуальнее с каждым днём, именно поэтому моё приложение будет первым в данном направлении.

9. Итоги исследования:Мне удалось обеспечить анонимную работу приложения со стороны клиента. Исходя из малочисленной аудитории моего проекта, 15 человек на данный момент, мне пришлось проводить опросы у простых людей на улице, 10 из 10 говорили, что они скачали бы его себе на телефон и пользовались бы им. 
10. Список использованной литературы

1. VK API(https://vk.com/dev/main)
2. Герберт Шилдт "Java 8. Полное руководство. 9-е издание"
3. Максим Боговик – Hibernate для самых маленьких и не только ( http://habrahabr.ru/post/132385/ )
4. Энтони Гонсалвес – “Изучаем Java EE 7”
5. https://ru.wikipedia.org/wiki/Вконтакте
6. https://ru.wikipedia.org/wiki/JSON

http://vk.com/invis_project  - сообщество вконтакте, здесь актуальные версии нашего разрабатываемого приложения.
 

Известно, что некоторым простым числом  p называют такое число, которое имеет ровно два делителя: 1 и p. В настоящее время среди различных разделов математики одной из наиболее актуальных проблем остается проблема нахождения закономерности в распределении простых чисел.  Интерес к проблеме обусловлен тем, что простые числа являются основой современной криптографии. Таким образом, они являются неотъемлемой частью жизни современного человека. Без них не обходится ни один процесс аутентификации, например, регистрация телефона в сети, банковские платежи и прочее.

Целью данной работы является написание эффективного по времени алгоритма вычисления простых чисел в заданном диапазоне от  M до N. Известно, что для эффективной программы требуется подходящая математическая составляющая алгоритма.

В ходе работы были обозначены следующие задачи:

• рассмотреть роль простых чисел в криптографии для анализа их взаимодействия между собой;
• построить новую модель вариации Скатерти Улама с целью выявления закономерностей в распределении чисел (Microsoft Excel);
• разложить нечетные числа на арифметические прогрессии для анализа свойств распределения простых чисел;
• ознакомиться с технологией программирования для выявления роли теории чисел в решениях алгоритмических задач (используем среду программирования CodeBlocks12);
• использовать полученные данные для оптимизации алгоритма;

В ходе работы мы придерживались методов экспериментально-теоретического уровня, а именно анализ, эксперимент и моделирование. Данные методы исследования помогают не только собрать факты, но проверить их, систематизировать, выявить неслучайные зависимости и определить причины и следствия.

Для создания новой модели вариации скатерти Улама мы обратились к программе Microsoft Excel. Принцип расположения чисел в спирали оставляем, но исключаем из спирали все четные элементы со сдвигом оставшихся нечетных элементов по часовой стрелке на свободные позиции.

Отметим, что на оригинальной скатерти была замечена следующая закономерность: простые числа выстраивались в длинные диагональные цепочки. На получившейся же скатерти явно выделяются четыре непрерывных ряда составных чисел. Каждая из представленных четырех последовательностей интересна тем, что разности соседних двух элементов составляют арифметическую прогрессию с d = 16. (Приложение 1)

Так же в ходе работы было выяснено и доказано, что множество простых чисел P (для p>3) является подмножеством множества F, где F состоит из элементов двух арифметических прогрессий S₁ и S₂ таких, что у обеих разность d=6, а первые элементы равны 5 и 7 соответственно. Данное свойство применимо как при решении задач (например, доказательство того, что p²-1 кратно 24)(Приложение 2), так и для оптимизации алгоритма поиска простых чисел.

В результате работы был получен эффективный по времени алгоритм. Благодаря полученным результатам математическая составляющая кода способствовала повышению скорости работы алгоритма более чем в два раза. (Приложение 3 и Приложение 4) Например, для значений M=1000000 и N=1100000 программа выдает простые числа в данном промежутке всего за 17 секунд (вместо 37 секунд). (Код программы в формате .txt - приложение 5, ссылка на среду программирования - приложение 6, используемый язык - С++)

Если говорить о дальнейших перспективах исследования, то, на наш взгляд, стоит обратить  внимание на разработку алгоритма шифрования данных на основе криптосистемы RSA, с возможными модификациями, если они будут способствовать оптимизации программы. Помимо этого, модель вариации Спирали Улама наталкивает на мысль, что нужно продолжать поиски закономерности, но уже не в множестве простых чисел, а чисел составных.

Литература

1)«Математика. Республиканский научно-методический журнал», С. Я. Серовайский,
2009
2)Научная статья «Зависимость распределения простых чисел» Р. А. Кипер, преподаватель ДВГМУ
3)«Простые числа. Криптографические и вычислительные аспекты», Р. Крэндалл,
К. Померанс, 2011

Приложения

1. https://drive.google.com/file/d/0BzTfhg4Irq10WTBuVWVrLVZuTE0/view?usp=sharing
2. https://drive.google.com/file/d/0BzTfhg4Irq10UEYzcHd2ZDhUVTA/view?usp=sharing
3. https://drive.google.com/file/d/0BzTfhg4Irq10Nk5ES0xQTHozVDQ/view?usp=sharing
4. https://drive.google.com/file/d/0BzTfhg4Irq10UGs1Wmk3RzZQbjg/view?usp=sharing
5. https://drive.google.com/file/d/0BzTfhg4Irq10dlpac0FxUVBZcGs/view?usp=sharing
6. http://www.codeblocks.org/

Теория конечных проективных плоскостей (КПП) – один из разделов математики, который продолжает достаточно интенсивно развиваться и в настоящее время. В этой теории на сегодня нерешённых задач, пожалуй, больше, чем решенных [1]. Для порядка 11 на сегодня известна дезаргова КПП [1], но не доказано, что она единственная. Если кто-либо сумеет построить другую, «новую» КПП порядка 11, то ему неизбежно придётся доказывать, что она не изоморфна известной. Но для этого нужно иметь достаточно удачное представление этой известной КПП порядка.

Кроме того, в теории КПП для каждой конкретной плоскости важно знать ее строение, в частности, k-дуги в ней. 

Цель работы: исследовать 8-дуги  в КПП порядка 11

Для достижения указанной цели необходимо решить следующие задачи:

1. познакомиться с элементами теории конечных проективных плоскостей (КПП), научиться строить КПП порядка 11 над конечным полем того же порядка [2]; рассмотреть группу коллинеаций изучаемой плоскости и важнейшие коллинеации этой группы [3]; разобраться в сведениях об опорных k-дугах для изучаемой плоскости при k =1, 2, 3, 4, 5, 6, 7 [3];
2. исследовать 8-дуги в той же плоскости.

На данный момент узлы часто появляются в математике (математическая теория турбулентности), физике (конструирование динамических систем и слоений), биологии (заузленные молекулы ДНК), поэтому задача распознавания тривиальности данного узла и, в конечном счёте, эквивалентности или различности узлов, весьма актуальна. Обычно она решается с помощью вычисления различных инвариантов, которые, как правило, являются сложными. Хотелось бы иметь простые, но информативные и наглядные инварианты. Цель работы: оценить, насколько число правильных раскрасок диаграммы узла в утолщенном торе тремя или более цветами, а также сам факт правильной раскрашиваемости, информативно. В работе использованы базовые понятия теории узлов, такие как «гомеоморфизм», «узел в утолщённом торе», «диаграмма узла», «инвариант», «правильная раскраска диаграммы узла». Поскольку вычисление числа раскрасок цветами в данном трехмерном многообразии до сих пор не выполнялось, работа является новой.
Для достижения поставленной цели необходимо решить следующие задачи:
1) Изучить основные нужные нам определения из теории узлов.
2) Составить таблицу о количестве правильных раскрасок диаграмм узлов в утолщенном торе, до сложности пять, используя множество, состоящие их трёх цветов.
3) Доказать теорему об инвариантности количества правильных раскрасок диаграмм узлов в утолщенном торе.
4) Проверить закономерность раскраски тремя цветами диаграммы узла в утолщенном торе.
Результатом работы является доказательство теоремы об инвариантности числа правильных раскрасок узлов в утолщённом торе и составленная таблица числа правильных раскрасок диаграмм узлов в утолщённом торе сложностью до 5 включительно. Некоторой закономерности раскраски тремя цветами диаграммы узла в утолщённом торе не найдено. Результаты данной работы могут послужить в дальнейшем изучения инвариантов узлов в современной теории узлов, которые имеют приложения в биологии, физике и химии.

Название научно-исследовательской работы: Математика времени через историю развития часов

ФИО автора работы: Лысенко Анастасия Сергеевна

Образовательное учреждение, в котором обучается автор работы: МБОУ «Гимназия № 21»

ФИО, должность и место работы научного руководителя: Лысенко Елена Валерьевна, учитель математики, МБОУ «Гимназия № 21»

Краткая постановка цели и задач исследования:

Цель работы – исследование наличия  математических задач в зависимости от вида часов.

Поставленная цель обозначила  следующие задачи:

-определить виды часов в зависимости от конструкции в историческом аспекте;

- дать характеристику часам и задачам, связанным с ними;

- подобрать, найти решение  или решить задачи с часами

- систематизировать и создать блоги, которые можно постоянно дополнять и обновлять.

Основной текст тезисов:

Человечество всегда отдавало себе отчет в том, что течение времени необратимо, но всегда пыталось измерять и регистрировать ход времени.

 Если говорить о времени, то, первое, что приходит в голову – это часы. Часы— инструмент для измерения продолжительности временных интервалов, в единицах, меньших чем одни сутки.

Выдвинув гипотезу, что почти к каждому виду часов можно найти задачи, связанные со временем, все исследование было построено на ее подтверждении.

Объект исследования – виды часов. Предмет исследования – задачи с различными часами.

Самые первые часы, были солнечные, гномоны. О времени судили по длине тени, отбрасываемой вертикальными предметами. Устройство солнечных часов основано на постоянном, равномерном вращении Земли вокруг оси и зависит от движения Солнца. Поэтому самым большим недостатком является его отсутствие в ночное время. Перелистав много книг и просмотрев много сайтов, мы не нашли ни одной задачи связанной с солнечными часами.

Водяные часы после солнечных часов занимали второе место по количеству и были самыми важными в этой группе простейших часов.Сосуд часов имел форму конуса, в нижней части его находилась трубка, через которую вытекала вода в специальный приёмник. Недостаток водных часов в том, что вода замерзает зимой и испаряется летом.

Задач, в которых бы фигурировали водяные часы, встретилась лишь одна на вычисление размера часов.

Помимо солнечных и водяных часов, появились и первые огневые – свечные часы. Эти очень простые часы в виде длинной тонкой свечи с нанесенной по ее длине шкалой, сравнительно удовлетворительно показывали время, а в ночные часы они еще и освещали жилища крупных сановников и правителей. Был и другой вид часов в вид шнура. Его пропитывали ароматическими средствами, и когда начинал идти запах – тогда прошло определенное количество времени. Задача, которую можно отнести к огненными часами также была найдена только одна, и   связана она с горением шнура на смекалку.

Чтобы подсчитывать одинаковые промежутки времени были созданы песочные часов. Недостатком, мешавшим широкому применению этих часов, был сравнительно короткий интервал времени, который можно было измерить, не переворачивая эти часы.

С песочными часами были найдены 4 задачи одного типа, на определение отрезка времени.

 Первое упоминание о механических часах содержится в византийских книгах конца 6-го века н.э. Знакомые нам механические часы изобретены в 1250 году. В шестнадцатом веке появились карманные часы, а в конце девятнадцатого века – наручные.

Провели эксперимент на наличие часов, именно механических у 75 десятиклассников: оказалось, что только у 20% опрошенных(15 человек) есть часы.

Самое большое количество задач существует с механическими часами, в силу их сложности конструкции. Здесь есть часы, имеющие две, три стрелки (40 задач), циферблат с числами, у некоторых настенных наличие боя (7) или маятника. Многие задачи порождены недостатками механических часов, имеющих склонность спешить, отставать или вообще останавливаться(18). Мы нашли большое количество задачи и систематизировали их по различным признакам, результаты представили в блоге.

Следующая веха – электронные часы. В связи с простотой настройки таких часов и легким определением времени, такие часы стали самыми популярными в наше время. Здесь тоже повезло найти 4 задачи.

Также упомянули в работе и о новых типах часов радиоактивные и атомные.

История развития часов насчитывает тысячелетия и с каждым видом часов появлялись задачи, связанные с расчетом времени, в зависимости от конструкции часов. Скорее всего, и с этими видами часов будут придуманы задачи.

Актуальность исследования: Актуальность данной темы в том, что понять природу времени пытаются тысячелетия, и я хотела бы внести свой вклад в эти исследования через поиск, анализ и решение задач с часами. Развитие часов прогрессирует быстрыми темпами, их точность становится почти идеальной, а наши знания о них обновляются значительно медленнее, поэтому возникает проблема поиска  нового способа для изучения природы времени.

Значимость и новизна исследования: новизна в том, что попытка систематизировать и создать коллекцию задач, в зависимости от вида часов не встречалась ранее. Значимость подтверждена тем, что обращение к блогам было чаще, чем предполагали, и одна из причин подборка задач, актуальных при подготовке к олимпиадам. [14,15].

Итоги исследования: Время – самое загадочное понятие. Через исследование задач на время, через историю развития инструмента, определяющего его, я сделала попытку понять природу времени. Задач огромное множество с часами, но фактически их можно разделить на группы только задачи с механическими часами, все остальные виды представлены лишь несколькими примерами.

Список использованной литературы.

1. Скляревский Е.С. Задачи, связанные со временем. [Электронный ресурс] // Арбуз. Занимательный мир чисел, букв, пикселей и заблуждений. URL: http://arbuz.uz/w_time.html (дата обращения: 25.01.2016)
2. Загадки про время. [Электронный ресурс] // Логические задачи и головоломки. URL: http://www.smekalka.pp.ru/time.html (дата обращения: 25.01.2016)
3. Аманда Вудвард. История часов [Электронный ресурс] // URL: http://sfw.so/1148964185-istoriya-chasov.html (дата обращения: 25.01.2016)
4. Козлова Е.Г. Сказки и подсказки: Задачи для математического кружка. – М.:МИРОС, 1995. 128 с. ( стр. 25, 33)
5. Способы измерения времени. [Электронный ресурс] // Часовой журнал 1 секунда. URL: http://1seconds.ru/istoriya-sozdaniya-chasov/sposoby-izmereniya-vremeni.html (дата обращения: 25.01.2016)
6. Перельман Я.И. Веселые задачи.   Перельман Я.И.   М.: Астрель: АСТ, 2003.— 287с. (Занимательная наука.)
7. Перельман Я.И. Веселые задачки и головоломки.   М.: Астрель: АСТ, 2010.— 382с. (Карманная библиотека.)(стр. 279-295)
8. Сэм Ллойд. Математическая мозаика М.: РИПОЛ, 1995.— 352с.(стр. 113,145)
9. Нагибин Ф.Ф., Канин Е.С.Математическая шкатулка, М.: Просвещение, 1998.— 160 с. (стр. 84)
10. Трошин В.В. Занимательные дидактические материалы по математике. Сборник заданий. М.: Глобус, 2008.— 282с. (стр.215-279)
11. Энциклопедия головоломок: Книга для детей и родителей. - М.: АСТ-ПРЕСС, 1997.— 320с.(стр. 108,172,206)
12. О времени. Логические задачи, головоломки, тесты на интеллект... [Электронный ресурс] // На все задачи есть ответ! URL: http://nazva.net/rubric/3/ (дата обращения: 25.01.2016)
13. Математические олимпиады и олимпиадные задачи  [Электронный ресурс] // Разное. Материалы Кировской ЛМШ, 2000 г, 6 класс. Задачи про часы URL: http://www.zaba.ru/cgi-bin/tasks.cgi?tour=books.sms6.chasy (дата обращения: 25.01.2016)
14. Математика времени. [Электронный ресурс] // URL: http://mathvremeny.blogspot.ru/ (дата обращения: 25.01.2016)
15. Механические часы и математические задачи. [Электронный ресурс] // URL: http://zadachischasami.blogspot.ru/ (дата обращения: 25.01.2016)

Создание программы для решения систем и квадратных уравнений.

Система создания, обработки и хранения неограниченных ландшафтов на основе треугольных сетей.

Автор: Кириллов Алексей Викторович, 11 «Б» класс МБОУ ФМЛ г. Сергиев Посад.

Научный руководитель: Барулина Надежда Николаевна, учитель информатики МБОУ ФМЛ г. Сергиев Посад.

Цели и задачи:

Исследовать частные свойства треугольных сетей и возможность их использования для представления поверхностей в цифровом виде; создать систему обработки ландшафта на их основе и определить её точность и эффективность.

Описание работы:

В настоящее время одной из первоочередных задач является симуляция различных процессов в цифровой форме. Несмотря на это, механизм представления трёхмерных ландшафтов за последнее десятилетие почти не изменился – используется квадратная сеть, узлы которой смещены по высоте. Однако у данной модели есть серьёзные недостатки. Автор предположил, что использование треугольной сети в качестве основы - оптимальный вариант. В работе приводятся результаты комплексного исследования и разработки системы, а так же некоторые наиболее наглядные его части.

Итоги исследования:

В процессе исследования, были изучены частные свойства треугольной сети, возможности по её преобразованию и хранению, создан процедурный алгоритм генерации и написана динамическая библиотека, включающая все наработки.

Полученная система показала хорошие результаты и может использоваться в качестве ядра систем навигации и игровых движков.

Список использованной литературы:

1. Денис Ольшин. Алгоритм «diamond-square» для построения фрактальных ландшафтов. ‒ http://habrahabr.ru/post/111538/
2. Михаил Фарленков. Ландшафты быстрого приготовления. ‒ http://www.uraldev.ru/articles/4
3. Amit Patel. Introduction to A* («Введение в А*»). ‒ http://www.redblobgames.com/pathfinding/a-star/introduction.html
4. 3D Lab. Fractal Terrains. ‒ http://www.ibiblio.org/e-notes/VRML/Terra/Terra.htm

Название научно-исследовательской работы: Изучение теории графов и решение задач про графы с цветными рёбрами, вывод чисел Рамсея: R(3;3), R(3;4), R(4;4).

 Автор работы: Александров Никита Владимирович

Образовательное учреждение: МАОУ «Лицей №14 имени Заслуженного учителя Российской Федерации А.М.Кузьмина»

 Научный руководитель: Неверовская Светлана Владимировна, учитель математики в МАОУ «Лицей №14 имени Заслуженного учителя Российской Федерации А.М.Кузьмина»

Цели: Изучить теорию графов и в частности графы с цветными рёбрами. Научиться применять основные методы теории графов при решении задач.

Задачи:

Проанализировать учебную и научную литературу с целью определения базовых понятий и степени изученности темы;

Освоить основные понятия теории графов;

Классифицировать типы задач по теории графов;

Выявить особенности задач по теории графов с цветными ребрами;

Научиться решать задачи олимпиадного характера по данной теме;

Вывести числа Рамсея (3;3), (3;4), (4;4)

Для достижения поставленных целей: изучил теоретическую базу по данной теме; научился решать олимпиадные задачи с применением теории графов; доказал некоторые свойства графов с цветными рёбрами; узнал информацию о числах Рамсея. самостоятельно вывел три числа Рамсея

Актуальность: Теория графов широко применяется в наше время. Например: в информатике и программировании, геоинформационных системах, в схемотехнике, химии и, конечно же, в математике. Многие олимпиадные задачи по математике рассчитаны на изучение специальных тем, которые не входят в школьную программу, в том числе и теория графов. Поэтому её изучение является актуальным

Значимость и новизна исследования: Развитие современной науки и неослабевающий интерес к изучению теории графов доказывают их привлекательность и важность для решения многих вопросов прикладного характера в различных областях.

Итоги исследования: В данной проектной работе были рассмотрены основные теоретические положения, связанные с теорией графов, показаны примеры решения задач, а также рассмотрена задача, в результате решения которой было найдено число Рамсея (3;3), число Рамсея (3;4) и число Рамсея (4;4).

Список использованной литературы:

Березина Л.Ю. Графы и их применение. Пособие для учителя. – М: Просвещение, 1979.

Березина Л.Ю. Графы с цветными ребрами. – «Квант», 1996, №6. Оре О. Графы и их применение. Серия «Современная математика». – М: «Мир», 2008.

Харари Ф. Теория графов. Под ред. Г.П.Гаврилова. – М: «Мир», 2003.

В современной школе математические науки с каждым днем все меньше привлекают внимание учеников. Именно в связи с этим обстоятельством школьники часто допускают ошибки при выполнении легких и интересных математических заданий. Особый страх у школьников вызывает построение графиков функций и решение уравнений и неравенств, содержащих переменную под знаком модуля. В данной работе я попытаюсь развеять этот напрасный страх и, тем самым, помочь школьникам более эффективно усвоить школьный материал.

Название работы: ” Моделирование и исследование клеточного автомата ‘Жизнь’ ”

Автор: Ушаков Михаил Алексеевич

Образовательное учереждение: ГБОУ Гимназия№261, 8 класс, г.Санкт-Петербург

Научный руководитель: Никольская Ольга Сергеевна, учитель информатики и математики

Краткая постановка целей : Моделирование математической игры "Жизнь", реализация новых правил и исследование взаимодействия колоний.

Основной текст тезисов:

Исседование посвящено математической игре “Жизнь”. Изучив материал, я реализовал алгоритм данной игры на языке программирования Pascal. Провел исследования различных конфигураций, а также расширил правила игы жизнь для исследования взаимодействия клеточных колоний разных видов.

Для создания приложения, я использовал среду разработки PascalABC.NET, Windows Forms и внутренние компоненты платформы .NET. Интерфейс приложения выполнен в классическом стиле компонент Windows. При запуске приложения в левой части окна пользователю представляется игровое поле. В правом верхнем углу находится настройка игрока (имя, цвет колонии), там же пользователю предоставляется возможность создавать новые виды колоний. Чуть ниже располагаются параметры игрового поля (ширина, высота) и кнопка запуска/остановки игрового процесса.

Актуальность исследования:

Данный проект может использоваться исследователями игры "Жизнь" в качестве редактора-конструктора конфигураций. Также с введением новых правил, его можно и использовать для изучения взаимодействия примитивных колоний микроорганизмов.

Итоги исследования :

В результатае проведения исследования, мне удалось создать приложение, позволяющее конструировать и изучать новые конфигурации математической игры "Жизнь".

При разработке приложения возникли некоторые трудности, связанные с созданием плавной анимации смены поколений в игре. Для решения этих проблем мне пришлось реализовать механизм буферизации изображения перед выводом на экран. В будущем я планирую развивать этот проект. Планируются следующие нововведения: добавится возможность изменения правила поведения колоний, сохранение и загрузка состояния, добавление на поле и сохранение в базу данных групп клеток, имеющих интересные свойства.

Список литературы:

1. Гарднер М. , Математические досуги: 2-е изд., испр. и доп. /Пер. c англ. Ю.А. Данилова под ред. Я. А. Смородинского. – М.: Мир, 2000.
2. Александров В. В. и др., ЭВМ: игра и творчество, «Машиностроение», 1989, 128 с.
3. Горячев А. В., Информатика. 8 кл.: учеб. для общеобразоват. учреждений в 2-х кн. Кн.1, «Баласс», 2012, 256 с.
4. Культин Н. Б., Delphi в задачах и примерах, «БХВ-Петербург», 2012, 288 с.
5. Культин Н. Б., Turbo Pascal в задачах и примерах, «БХВ-Санкт-Петербург», 2000, 256 с.
6. Рапаков Г. Г., Turbo Pascal для студентов и школьников, «БХВ-Петербург», 2011, 352 с.
7. Фленов М. Е., Библия Delphi, «БХВ-Петербург», 2014, 688 с.

6 класс, МБОУ «Гимназия им. Н.Г. Басова при ВГУ», Воронеж
Науч.руководитель - Белоусова А.Г.
учитель математики, МБОУ «Гимназия им. Н.Г. Басова при ВГУ», Воронеж

Человек в процессе общения (получения акустической информации) является объектом информационного воздействия. В результате этого воздействия у человека формируется его собственное представление о содержании информации, получаемой им. Процесс формирования такой информационной модели содержит, на наш взгляд, два уровня восприятия информации – сознательный (когда на основании осознанного анализа содержания информации человек формирует образы объектов и процессов о которых ему говорят) и бессознательный (когда информационное воздействие вызывает в человеке ассоциативную цепь создания настроения, и этот процесс никак слушателем не контролируется и не управляется). Ввиду того, что в современном мире человек находится под воздействием огромного потока информации, актуальной является возможность определять, оказывается ли на человека несанкционированное (со скрытыми от него целями) воздействие.
Целью исследования является – установить, возможно ли, оказывать на слушателя акустическое информационное воздействие, с целью скрытно от слушателя сформировать у него заданное настроение и поведенческие реакции.
В данной работе поставлена задача – показать возможности фонетического строя произведения в формировании настроения слушателя на подсознательном уровне, не зависимо от субъективного восприятия смысла услышанного.
В исследовании разработана методика выводящая процесс познания смыла в область бессознательных ассоциативных транзакций «звук-цвет-настроение».
Для анализа процессов создания настроения слушателя под воздействием информационного акустического воздействия нам показалось интересным выбрать тот вид воздействия, который гарантировал бы отсутствие сознательного компонента усвоения информации. Таким воздействием является иностранный язык неизвестный слушателю. Мы выбрали английский язык и проанализировали насколько точно настроение, возникающее у слушателя, соответствует действительному содержанию определенного поэтического произведения.
Объектом исследования выбраны два стихотворения – «My heart's in the Highlands» Роберта Бернса и перевод «В горах мое сердце» С.Я.Маршака.
Схема анализа была следующая:
1. Количественно определен состав воздействия, т.е. количество различных фонетических звуков.
2. Проведена процедура выделения избыточной (над нормальной) частоты присутствия звуков  и далее работали только со звуками, превышающими нормальную частоту.
3. По известным таблицам  построены цветовые диаграммы звуков.
4. Интерпретированы цветовые диаграммы, связав их с эмоциональными данными.

В работе показано, что при открытом акустическом воздействии на слушателя с помощью естественного языка можно оказывать несанкционированное (скрытое по целям) воздействие на слушателя. Результатом такого воздействия может быть формирование у слушателя нужного эмоционального состояния, а значит, и поведенческих реакций.
Перспективными в этой области являются исследования влияния фонетического состава языка на психо-эмоциональные характеристики носителя и слушателя, что, возможно, актуальным является для изучения поведенческих реакций. Кроме того, представленная методика позволяет реализовать компьютерный анализ любого цвето-звукового воздействия на человека (в т.ч. реклама на естественном языке, сопровождение компьютерных игр и др.) на предмет присутствия в нем несанкционированного психо-информационного воздействия на естественном языке.

Глущенко Никита Сергеевич

МАОУ гимназия № 10 им. А. Е. Бочкина

Научный руководитель Слаушевская Мария Евгеньевна, учитель информатики МАОУ гимназия № 10 им. А. Е. Бочкина

В истории развития техники известно много механизмов, которые позволяют переводить вращательное движение мотора в поступательное. Поступательное движение – это прежде всего движение ног человека, лап животных  в реальном мире. Современные технологии на сегодняшний день стремятся воспроизвести именно эти движения, придуманные самой природой. Например, в робототехнике конструируют такие модели, как роботы – пауки, гепарды и, конечно, андроиды.

В спортивной робототехнике тоже достаточно популярны шагающие роботы, в которых и применяются механизмы, преобразующие вращательное движение в поступательное, крутящий момент мотора в поступательное движение ног робота. Такие механизмы иногда называют «шагающими».  В соревнованиях обычно побеждает тот робот, который быстрее двигается. Участники достигают этой цели опытным путем, подбирая в конструкции робота балки различной длины и зубчатые передачи с различными передаточными числами. Но такой способ требует больших временных затрат, и не всегда будет достигнут хороший результат. Гипотеза: применение программного средства для расчета наилучших вариантов балок и моторов позволит оптимизировать подбор деталей при конструировании «шагающего» механизма.

Цель: Создать программный продукт для расчета оптимальной конструкции «шагающего» механизма.

Задачи:

1. Отобрать самые популярные ходячие механизмы и выявить математические и физические закономерности конструкции.
2. Создать математическую модель задачи определения скорости движения «ходячего» механизма в зависимости от мощности мотора и длины используемых балок.
3. Построить графическую модель работы механизма
4. Реализовать все полученные модели в одном программном продукте.

Объект исследования: механизм, преобразующий вращательное движение в поступательное. Предмет исследования:  математические и физические закономерности конструкции механизма.

Методы исследования: анализ, поиск математических закономерностей, математическое и компьютерное моделирование, программирование.

В разработанной компьютерной модели реализованы две самых популярных классических конструкции:

• Механизм Хойкена ( подобие механизма Чебышева),
• Механизм Кланна.

Новизна компьютерной модели заключается в том,  что в ней наглядно представлены расчеты зависимости скорости передвижения механизма в целом от скорости вращения центральной оси мотора  и длины балок, используемых в конструкции «ноги». Полученное программное средство действительно позволяет облегчить работу механика при подготовке робототехнического проекта к соревнованиям, выполняя сначала расчеты элементов конструкции.

Список литературы:

1. Артоболевский И. И. Теория механизмов и машин: Учеб. для втузов. — М.: Наука. Гл. ред. физ.-мат. лит., 1988. — 640 с.
2. Дзенушко Дайнис. Изучение "Шагающих" механизмов - http://tm.spbstu.ru

Муниципальное автономное общеобразовательное учреждение Лицей№2, г.Пермь

Математический анализ и моделирование роста микроорганизмов

Научно-исследовательская работа:
Ласкавого Николая
Научный руководитель:
кандидат физико-математических наук, старший преподаватель, доцент кафедры общей физики в Пермском Государственном Научном Исследовательском Университете Гаврилов К.А.

Цель работы: провести математический анализ и смоделировать процесс роста родококков.

В начале работы я обсудил со своим научным руководителем, кандидатом физико-математических наук, старшим преподавателем, доцентом кафедры общей физики в Пермском Государственном Научном Исследовательском Университете Гавриловым К.А.тему своей будущей работы.
По его рекомендации я самостоятельно изучил некоторые темы из начала математического анализа, такие как: дифференциал функции и его приложения, неопределённый интеграл, дифференциальные уравнения и элементы математической статистики.
Совместно с Гавриловым К.А. мы вывели формулы экспоненциального и сигмовидного роста бактерий.
Научный руководитель предоставил мне экспериментальные данные о росте родококков в мясопептонном бульоне и на минеральной среде с н-гексадеканом.
С помощью программ Microsoft Office Excel и GNUPLOT я смоделировал аппроксимированные графики к экспериментальным графикам.

Вывод

Рост родококков в мясопептонном бульоне и минеральной среде с н-гексадеканом происходит по тем же самым законам, как и рост любых других микроорганизмов и, поэтому, он подчиняется математическому анализу и моделированию.
В свою очередь, моделирование процессов роста родококков может помочь определить сроки очистки почвы или водоемов от загрязнения углеводородами при техногенных катастрофах.
Коэффициент прироста Rhodococcus ruber ИЭГМ 219 на мясопептонном бульоне выше, чем на минеральной среде с н-гексадеканом, следовательно, для каждого штамма бактерий благоприятна своя питательная среда, и это необходимо учитывать при решении задач устранения загрязнения окружающей среды.

Список литературы

1. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы. — М.: Наука. Главная редакция физико-математической литературы, 1980. —496 с.
2. Ризниченко Г. Ю.Математические модели в биофизике и экологии. — Москва-Ижевск: Институт компьютерных исследований, 2003, 184 стр.
3. Воробьёв А.В., Быков А.С., Пашков Е.П., Рыбакова А.М. Микробиология: Учебник. —2-е изд., перераб. И доп. — М.: Медицина, 2003. —336 с.
4. Интернет ресурс

В наши дни теория вероятностей занимает одно из первых мест в прикладных науках по широте своей области применения, "нет почти ни одной естественной науки, в которой так или иначе не применялись бы вероятностные методы"( Вентцель Е.С. Теория Вероятностей)

Современное развитие теории вероятностей характерно всеобщим подъемом интереса к ней и резким расширением круга ее практических применений. За последние десятилетия теория вероятностей превратилась в одну из наиболее быстро развивающихся наук, теснейшим образом связанную с потребностями практики и техники.

Мы стали свидетелями рождения новых и своеобразных методов прикладной теории вероятностей, появление которых связано со спецификой исследуемых технических проблем. Речь идет, в частности, о таких дисциплинах, как "теория информации" и "теория массового обслуживания". Возникшие из непосредственныхпотребностей практики, эти разделы теории вероятностейприобретают общее теоретическое значение, а круг их приложения постоянно увеличивается. Моя работа раскрывает прикладное значение теории вероятности для решения задач в военной области.

Работа посвящена вкладу ученых-математиков в нашу Победу в Великой Отечественной войне. В работе рассмотрен как вклад каждого отдельно взятого ученого математика, так и значимость теоритических открытий в области математики в годы войны, позволивших реально приблизить Победу. Это и теория стрельбы, и расчеты непотопляемсти судна, и теория взрыва, и теория штопора и шимми. Практическое применение этих теорий раскрыто в моей работе.