Тезисы:

Любая теория современной науки считается верной, пока не создана следующая. Это своеобразный факт развития науки, который имеет подтверждение. Например,  алхимия стала в последствии химией. Такова судьба всех наук, и геометрия не исключение. Традиционная геометрия Евклида переросла в геометрию Лобачевского. В данной работе был проведен сравнительный анализ геометрии Н. И.Лобачевского и геометрии Евклида.                                  В первой главе данной работы было проведено анкетирование среди 9-11 классов, чтобы понять, знают ли школьники о существовании другой геометрии. Стандартный школьный курс предусматривает изучение только геометрии Евклида, поэтому, учащимся, при знакомстве с неевклидовой геометрией, достаточно трудно поверить, в то, что через точку не лежащую на данной прямой можно провести более одной прямой, параллельной данной. Как мы выяснили, учащиеся не понимают, какую геометрию они изучают. Так, 40% опрошенных высказалось за то, что мы изучаем геометрию Лобачевского в школе.                                                                    Вторая глава работы посвящена исследованию геометрии Евклида, в ней также рассматриваются пять великих постулатов, предложенных самим Евклидом в его "Началах геометрии ". Со временем, пятый постулат попал под сомнение и математики начали полагать, что это вовсе не постулат, а теорема. К сожалению или к счастью, но  попытки доказательства пятого постулата не увенчались успехом. Именно тогда и рождается новая геометрия. Геометрия Н.И. Лобачевского.                                                                                                                            В третьей главе работы рассматриваются основные аспекты и модели геометрии Лобачевского, а также практическое применение этой геометрии в космологии и механике.                В четвертой главе данной работы я произвела сравнительный анализ геометрии Лобачевского и Евклида. В данном проекте я привожу три сравнительных таблицы. Сравнительный анализ с математической точки зрения, сравнительный анализ некоторых теорем в геометрии Лобачевского и Евклида, а также провожу обобщенное сравнение геометрий.                                                                                                                                 В пятой главе я подвожу итоги проделанной работы. Как мне кажется, цель и задачи проекта были достигнуты. Был проведен сравнительный анализ геометрии Лобачевского и геометрии Евклида. Гипотеза проекта подтвердилась. Действительно, в геометрии Лобачевского и Евклида различаются только те теоремы, которые опираются на V постулат.

Новые результаты: В геометрии Лобачевского и Евклида найдены и определены основные отличия. Был проведен сравнительный анализ этих геометрий не только с математической, но и с некоторой философской стороны. В данной исследовательской работе приводится элементарное доказательство некоторых теорем в геометрии Лобачевского, понятные даже школьнику.

• Данный проект может быть применен учителями на уроках и дополнительных занятиях по геометрии в старших классах.
• Данный проект самостоятельно могут использовать ученики для расширения своего кругозора и знаний по геометрии.

Тема моей научно-исследовательской работы "Удвоение куба". Меня привелекла эта работа тем, что в ней множество неразгаданной информации, которую можно изучить.

Математические задачи возникающие в нашей жизни разнообразнны и многочисленны. При помощи изучении задач мы делаем новые открытия в какой-либо области.

Актуальность данной темы определяется тем, что  геометрия окружает нас везде в нашей жизни.

В моей работе я разобрала несколько способов задачи удвоение куба. И  с помощью техники оригами смогла удвоить несколько кубов.

Удвоение куба применяют в строительстве, архитектуре, дизайне и повсюду.

В итоге, я изучила историю возникновения, методы решения и применение задачи об удвоение куба. На мой взгляд эта задача важна в нашей жизни.

    В определенных математических кругах сложилось мнение, что Ферма был неправ, утверждая, что нашел простое доказательство своей знаменитой теоремы.Цель данного исследования – доказать справедливость слов французского математика для третьей степени теоремы. Приводится доказательство Великой теоремы Ферма для третьей степени. Основной идеей доказательства является опора на утверждение: если разность третьих степеней двух натуральных чисел кратна 3, то разность степеней этих чисел кратна и 9. При доказательстве используются методы элементарной алгебры, а также методы теории сравнений, в частности, теорема Эйлера.

Универсальная среда моделирования многоагентных систем “CellMachine”

Автор: Василенко Егор Олегович, Московская область, г. Одинцово, МБОУ Одинцовский лицей №10

Научный руководитель: Зорина Елена Алексеевна, учитель информатики Одинцовского лицея №10

Цель: разработать универсальную библиотеку для компьютерного моделирования работы алгоритмов многоагентных систем.

Задачи: изучить существующие многоагентные алгоритмы и средства их моделирования с целью выявления их основных недостатков, а также необходимого для библиотеки функционала. Выбрать платформу для создания библиотеки. Написать библиотеку, включив в нее весь необходимый функционал. Реализовать с помощью библиотеки широко известные, а также авторские алгоритмы. Представить результаты работы широкой аудитории.

Методы исследования: изучение существующих решений, их анализ с целью выявления востребованного для системы моделирования функционала.

Репозиторий с исходным кодом среды находится в открытом доступе на ресурсе GitHub по адресу https://github.com/CellMachine/source

Установка и работа со средой: для начала работы достаточно скачать исходный код с https://github.com/CellMachine/source/blob/master/CellMachine.js и подключить к html-файлу через тег "script". Для создания моделей используется API, описанный в документации репозитория на GitHub.

Актуальность: разработка алгоритмов многоагентных систем не может проводиться без эффективных средств компьютерного моделирования, именно поэтому имеет значение наличие инструмента моделирования, который смог бы найти широкое применение среди исследователей.

Значимость и новизна: до сих пор не существует ни одного доступного для освоения любым заинтересованным специалистом инструмента, нацеленного на виртуальное моделирование многоагентных систем, взаимодействующих с внешней средой. Проект CellMachine - первый, совмещающий в себе клеточный автомат и широкие возможности для описания общения агентов и их взаимодействия с окружающей средой.

Итоги исследования: в результате была разработана универсальная среда для моделирования многоагентных систем и клеточных автоматов CellMachine. С помощью библиотеки были реализованы как известные алгоритмы (элементарные клеточные автоматы, муравьиная колония), так и авторские (модель битвы, парад роботов).

На ресурсе “Хабрахабр” опубликована статья (https://habrahabr.ru/post/311196/), посвященная библиотеке и алгоритму моделирования битвы, вызвавшая интерес у читателей.

Общедоступен репозиторий с исходным кодом на GitHub (https://github.com/CellMachine/source), куда помещен исходный код библиотеки.

Был создан официальный сайт проекта http://cell-machine.com. Посетив его, можно ознакомиться с примерами алгоритмов и исходным кодом их реализаций.

Список использованной литературы

1. Тоффоли Т., Марголус Н. Машины клеточных автоматов: Пер. с англ. - М.: Мир, - 280 с., ил.
2.  Флэнаган Д. Подробное руководство: Пер. с англ.– СПб: Символ Плюс, 2008. – 992 с., ил.
3.  Wolfram, A New Kind of Science: Champaign: Wolfram Media, 2002. - 1197 с., ил.
4.  Dorigo, T. Stützle. Ant Colony Optimization: MIT Press, 2004.
5.  Джон фон Нейман. Теория самовоспроизводящихся автоматов: Пер. с англ. - М.: Мир, 1971. - 48 с., ил.
6. Рафаэлло Ч. Графика на — СПб.: Питер, 2013. — 272 с., ил.
7. http://rileyjshaw.com/terra/ - описание и документация библиотеки js
8. https://learn.javascript.ru/ - справочник по языку JavaScript

Модель битвы, написанная с использованием CellMachine

Элементарный клеточный автомат

Коллективное поведение агентов

Удивительный треугольник Рело

Автор: Щувайло Дмитрий Сергеевич 8 класс

МБОУ “ Школа- гимназия №10 им. Э.К. Покровского”

Научный руководитель: Кулькова Людмила Михайловна , учитель математики МБОУ “ Школа- гимназия №10 им. Э.К. Покровского”

Цель работы: исследовать треугольник Рело как фигуру постоянной ширины и выяснить практическое применение его свойств .

Задачи: изучить литературу по данному вопросу ; изучить свойства и области применения треугольника Рело; опытным путем доказать, что треугольник Рело – это фигура постоянной ширины, определить ,где треугольник Рело встречается в жизни; сконструировать модель машины с колесами в форме треугольника Рело.

         Темой нашей прошлогодней исследовательской работы были углы. В этом году мы решили исследовать треугольники – самые простые замкнутые прямолинейные фигуры. Треугольник одна из первых фигур, свойства которых человек узнал еще в глубокой древности. Так как из всех многоугольников только треугольник является жесткой фигурой, он чаще других фигур применяется в практической жизни. Изучая треугольники на уроках геометрии, мы заинтересовались их разнообразием и применением в жизни. Особый интерес у нас вызвало изучение треугольника Рело, после прочтения научно- фантастического рассказа Пола Андерсона “ Треугольное колесо”.

     Гипотеза: треугольнику Рело присущи свойства обеих геометрических фигур, используемых при его построении и кроме того он имеет ряд собственных свойств , которые используются в технике.

   Для реализации цели и задач исследования мы использовали следующие методы: теоретический анализ литературы, сравнения, измерения, построение, наблюдение, фотографирование, моделирование.

   Актуальность проблемы состоит в том, что результаты наших исследований могут найти новое применение в технике и автомобилестроении.

   В ходе исследования мы доказали, что треугольник Рело -фигура постоянной ширины и имеет наименьшую площадь среди фигур этого класса. Также определили область применения треугольника Рело и попытались найти новые. Сконструировали макет машины с колесами в виде треугольника Рело и испытали ее на макете труднопроходимой дороги.      

   На основании проведенных исследований пришли к заключению ,что круг- не единственная фигура постоянной ширины, исследуемый треугольник Рело также принадлежит к этому классу. Он обладает всеми свойствами, характерными для фигур этого класс.       Опытным путем доказали, что треугольник Рело является фигурой постоянной ширины и имеет наименьшую площадь.           Область применения   треугольника Рело очень разнообразна , от автомобильных двигателей и техники, до архитектуры, дизайна и ювелирных изделий, а также часто используется как логотип. Использование треугольника Рело в качестве колес машины доказывает, что такие колеса будут легко двигаться по труднопроходимым дорогам.

     Выдвинутая нами гипотеза о свойствах треугольника Рело нашла свое подтверждение. Теоретическая значимость исследований состоит в описании, всестороннем анализе, сопоставлении свойств геометрических фигур, опережающем изучении формул площадей фигур.

   Полученные в ходе исследования результаты могут быть использованы для дальнейших исследований и испытаний. Мы рассмотрели треугольник Рело как геометрическую фигуру, в дальнейшем мы хотим исследовать его с точки зрения физики и применения треугольных колес для конструирования модели лунохода и марсохода.

                   Список использованных источников

1. Геометрия. 7-9 классы : учеб. Для общеобразоват. организаций /[ Л. С. Атанасян , В.Ф. Бутузов, С.Б. Камодцев и др.].- 5-е изд. - М.: Просвещение, 2015.-383с.
2. http://www.booklot.ru/authors/anderson-pol-uilyam/book/treugolnoe-koleso/content/608639-pol-anderson-treugolnoe-koleso/
3. https://ru.wikipedia.

Автор: Конышев Даниил Андреевич. 8 класс. МКОУ "Ирбитская общеобразовательная  школа № 9".  г.Ирбит, Свердловская область.

Научный руководитель: Кузьмин Глеб Юрьевич, студент 2-го курса ФАКИ МФТИ

ТЕЗИСЫ.

Постановка задачи.

Стандартно, задача нахождения общей формулы корней квадратного уравнения $A{x}^2+Bx+C=0$ решается методом выделения полного квадрата с получением единственной типовой формулы:  ${х}_{1,2}=\frac{-В\pm \sqrt[]{B^2-4AC}}{2A}$   [1] [2]  Метод выделения полного квадрата для выражений с многочленами не единственный, поэтому при нахождении общей формулы корней квадратного уравнения можно дополнительно привлекать разные способы получения или тождественного преобразования исходного уравнения. Один из них - метод вынесения общего множителя за скобки. Сформулируем задачу:  найти корни квадратного уравнения с привлечением метода вынесения общего множителя за скобки; провести анализ полученного решения..

Найденный в работе способ решения.

Решение обеспечивается добавлением в уравнение двух слагаемых с переменной "х":   $+kx-kx$,  где k - неизвестный числовой коэффициент. В этом состоит основное отличие от стандартного способа, в котором добавляются числовые слагаемые.  Вынесем множители ("Ах" и "k") за скобки:  $Ax\left(x+\frac{B+k}{A}\right)-k\left(x-\frac{C}{k}\right)=0$   Введем условие равенства  $\frac{B+k}{A}=-\frac{C}{k}$, необходимое для дальнейшего преобразования уравнения. После этого квадратное уравнение сводится к 2-м видам: $\left(Ax-k\right)\left(x-\frac{C}{k}\right)=0; \left(Ax-k\right)\left(x+\frac{B+k}{A}\right)=0$    Из условия равенства методом выделения полного квадрата находим неизвестный коэффициент k,  и подставляем его в корни этих уравнений.  Заканчиваем решение и независимо получаем две формулы нахождения корней квадратного уравнения:

${х}_{1,2}=\frac{-B\pm \sqrt{B^2-4AC}}{2A}$      (1) ;      $x_{1,2}=\frac{2C}{-B\pm \sqrt{B^2-4AC}}$           (2) ;  

Кроме этого способа решения, в работе найден еще один вариант независимого получения формул (1) и (2):  способом умножения двух линейных уравнений.

Анализ полученного решения.

• Доказана тождественность корней уравнения, вычисляемых по формулам (1) и (2)
• Найдено взаимное тождественное преобразование формул (1) и (2)
• Доказано, что корни уравнения по формуле (2) соотвествуют формулам Виета и разложению квадратного трехчлена на множители
• Выполнен анализ частных случаев для коэфициентов А=0 или С=0

Выводы.  В отличии от стандартного способа, предложенный способ решения квадратного уравнения позволяет независимо найти не одну, а две формулы вычисления корней квадратного уравнения.  Значения корней, полученные по этим формулам, тождественны. Формула (1) совпадает с формулой типового решения. Формула (2) в литературе не обнаружена. За исключенем частных случаев А=0 или С=0, корни квадратного уравнения можно равнозначно вычислять или по формуле (1), или по формуле (2). Для случаев А=0 или С=0 формулы (1) и (2) взаимно дополняют друг друга.

Заключение. Предложенный способ решения и формула (2) в литературе не найдены. Информация для анализа и сопоставления взята из учебников и справочников по элементарной математике. Данная работа может быть использована для справочных материалов по квадратным уравнениям.

Литература.

1. Выгодский М.Я. Справочник по элементарной математике, М., 2006 г

2. Википедия (квадратное уравнение) hthttps://ru.wikipedia.org/wiki/Квадратное_уравнение 

1. Программный комплекс для моделирования загрязнения окружающей среды

2. Автор: Домашенко Мария Сергеевна

3. МАОУ лицей 102 города Челябинска

4. Научный руководитель: Пашнин Андрей Александрович, педагог дополнительного образования МАОУ лицей 102 города Челябинска

5. Цель проекта: Разработка программного комплекса способного моделировать устойчивую картину  распространения загрязнений в атмосфере с помощью алгоритмов клеточных автоматов.

Задачи проекта:

1. Разработать математическую модель и алгоритм моделирования загрязнения атмосферы c  использованием  клеточных алгоритмов. 
2. Реализовать данный алгоритм в программной среде Visual Basic.
3. Разработать дружественный графический интерфейс (GUI).
4. Протестировать программу на примерах Челябинска и других городов.

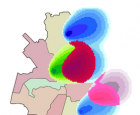
6. Программный комплекс, способный моделировать устойчивую картину распространения загрязнений в атмосфере. Данный проект необходим для того, чтобы учитывать предполагаемое воздействие загрязнений на окружающую среду при планировании строительства новых предприятий, или для моделирования картины загрязнения от существующих предприятий при проектировании новых жилых районов. С учетом входных данных, таких как роза ветров, координаты загрязнителей, уровень загрязнения и уровень поглощения, моделируется след загрязнения, отображаемый в программе цветом. Наложение загрязнений разных типов так же отображается в модели согласно разработанной палитре.

7. При планировании строительства новых предприятий необходимо учитывать предполагаемое воздействие на окружающую среду, в первую очередь на воздух жилых кварталов. Для того чтобы оценить предполагаемое загрязнение, необходимо смоделировать рассматриваемую ситуацию. Для строительства жилых районов в благоприятных для проживания местах нужно иметь модель загрязнения выбросами уже существующих предприятий. В этом заключается актуальность компьютерной модели, позволяющей моделировать устойчивую картину загрязнения атмосферы.

8. Новизна нашей работы заключается в том, что разрабатываемая программа позволяет определять области пересечения загрязнений разных типов и учитывать их поглощение окружающей средой.

9. Результаты:

1. Разработана математическая модель и алгоритм моделирования загрязнения атмосферы c  использованием  клеточных алгоритмов.
2. Алгоритм реализован в программной среде Visual Basic.
3. Разработан дружественный графический интерфейс.

4. Программа успешно протестирована на примере городов Челябинска и Магнитогорска. Алгоритм показал адекватные результаты: распространение загрязнений происходило по площадям эллиптической формы по направлению розы ветров. Пересечение разных типов загрязнений верно указывалось цветом.

10. Список использованной литературы:

1. Хейес Б. Клеточный автомат // В мире науки, 1984, № 5.
2. Тоффоли Т., Марголус Н. Машина клеточных автоматов. М.; Мир, 1991. 280 с.
3.  Минский М. Вычисления и автоматы. М.: Мир, 1971.
4. Вирт Н. Алгоритмы и структуры данных. СПб.: Невский диалект, 2001.

Генерация неизоморфных корневых деревьев на основе двоичных кодов.

Недорезов Пётр Владимирович, МБОУ «Гимназия №1 им. В. И. Ленина».

Руководитель: В. В. Филаретов, доктор технических наук, Ульяновский Государственный Технический Университет, ответственный редактор международного сборника научных трудов «Синтез, анализ и диагностика электронных цепей».

Задачи: Задача перечисления неизоморфных корневых деревьев относится к числу классических задач теории графов [1,2]. Рид [3] рассмотрел двоичный код и код уровней для непомеченных (без нумерации вершин) корневых деревьев.

Отечественные и зарубежные специалисты заинтересовались задачей перечисления (генерации) неизоморфных корневых деревьев почти одновременно – в конце 70-х годов прошлого века [4,5,6]. Исходными посылками к исследованию в работе [5] были теоретические работы [1,2]. В работах, доведённых до программной реализации, использовался бинарный (двоичный) [4] код и код уровней [6]. Совершенствование алгоритмов генерации деревьев и соответствующих программ продолжается до сих пор [7-12].

В данной работе предлагаются алгоритмы и программы генерации двоичных кодов корневых помеченных (с нумерацией вершин) деревьев, а также преобразования их двоичных кодов в векторы начальных вершин [9,10] для последующей проверки на старшинство с помощью подпрограммы testing [11].

Тезисы: Генератор двоичных кодов корневых деревьев. Работа генератора основана на последовательном преобразовании исходной комбинации 111...1000…0 в последующие комбинации, имеющие меньшее десятичное значение, вплоть до комбинации 101010…10. Каждая комбинация получается из предыдущей путем сдвига вправо последней единицы или не только ее, но и предшествующих ей единиц. При этом образуются все возможные двоичные числа с одинаковым числом единиц и нулей.

Сравнение способов представления корневых деревьев по числу генерируемых комбинаций. Во втором столбце указано количество лексикографических комбинаций (ЛГ-комбинаций) чисел натурального ряда, соответствующих векторам начальных вершин [9,10]. Эти ЛГ-комбинации также получены экспериментально [11] и являются совокупностью старших представителей (неизоморфных деревьев) и младших представителей (изоморфных деревьев). Количества двоичных кодов для корневых деревьев, рассчитанные по приведенной в данной работе программе [12], помещены в третий столбец табл. 1 [9].

Таблица 1. Количество ЛГ-комбинаций двоичных и ярусных кодов

для неизоморфных корневых деревьев

Число вершин	ЛГ– комбинации	Двоичные коды	Ярусные коды	Деревья [1]
4	4	5	4	4
5	12	14	9	9
6	39	42	23	20
7	128	132	66	48
8	424	429	210	115
9	1424	1430	733	286
10	4855	4862	2781	719
11	16788	16796	11378	1842
12	58777	58786	49864	4766
13	208002	208012	232769	12486
14	742889	742900	1151915	32973

Как видно, значения второго и третьего столбцов почти совпадают, что указывает на близость алгоритмов на основе векторов начальных вершин и двоичных кодов по сложности. Для получения вектора начальных вершин из ярусного кода необходима трудоёмкая порядковая нумерация вершин, а объем генерируемых комбинаций ярусных кодов оказывается существенно большим (табл. 1). Немаловажно, что алгоритм на основе векторов начальных вершин также более пригоден перечисления корневых деревьев вручную, поскольку лексикографические комбинации генерируются по простому закону, и легко проверяются на старшинство визуально [11].

Алгоритм преобразования промежуточного кода корневого дерева в вектор начальных вершин. Основан на последовательном добавлении строк (ветвей) промежуточного кода к нулевой строке (стволу). Вектор начальных вершин num формируется итеративно – по мере добавления строк к нулевой строке или текущему вектору num, содержащему поддерево, сформированное на предыдущих шагах подсоединения.

Программная реализация на языке Си. Вставки в текущий вектор num выполняются в ЛГ-порядке по правилу: номера, равные и большие позиции вставки, увеличиваются на единицу. Для ЛГ-вставки используется подпрограмма lexin. Алгоритм преобразования промежуточного кода в вектор начальных вершин реализован в подпрограмме transform.

Актуальность исследования: Проблема симметрий, усложняющая или делающая невозможным общее решение задачи структурного синтеза электронных цепей [9], обусловлена катастрофическим порождением изоморфных (избыточных) структур. При этом требуется генерация деревьев с номерами вершин, соответствующими топологии синтезируемой схемы. Неизоморфные корневые деревья используются, например, для пространственной ориентации робота [13], отображения произвольных иерархических структур и т. д. Генерация неизоморфных корневых деревьев в кодах, содержащих номера вершин, не рассматривалась до недавнего времени [11,12].

Значимость и новизна исследования: Предложен десятичный код в виде последовательности строк-путей дерева, занимающий промежуточное положение между двоичным кодом и вектором начальных вершин. Промежуточный код позволяет восстановить помеченное корневое дерево, более удобен для распознавания и определения глубины корневого дерева, чем обычно используемый в алгоритмах уровневый код.

Итоги: Разработаны алгоритмы и программы генерации двоичных кодов корневых деревьев, а также преобразования двоичного кода в промежуточный код и промежуточного кода в вектор начальных вершин корневого дерева.

Время генерации неизоморфных корневых деревьев при добавлении одной вершины увеличивается примерно в три раза, что не уступает самым быстрым известным программам [6,7] и определяется числом генерируемых деревьев. Количество сгенерированных неизоморфных деревьев в диапазоне вершин 4–17 совпадает с нашими расчётами по рекурентной формуле [1] и данными таблицы [2], что подтверждает правильность генерации двоичных кодов и их преобразования в векторы начальных вершин.

Список использованной литературы:

1) Otter R. The Number of Trees // The Annals of Mathematics, 2nd Ser.- 1948.- Vol. 49, No. 3.- P. 583-599.

2) Харари Ф. Теория графов.– М.: Мир, 1973.– 300 c.

3) Read R.C. How to grow trees // Combinatorial Structures and their Applications.– New York: Gordon and Breach, 1970.

4) Диниц Е.А., Зайцев М.А. Алгоритмы генерации неизоморфных деревьев // Автоматика и телемеханика.– 1977.– Вып. 4.– С. 121–126.

5) Kоzina A.V. Coding and generation of nonisomorphic trees // Plenum Publishing Corporation.– 1980.– Translated from Kibernetika.– 1979.– N5.– P. 38–43.

6) Beyer T., Hedetniemi S. M. Constant time generation of rooted trees // Journal of the Society for Industrial and Applied Mathematics: Computation.– 1980.– Vol. 9, no. 4.– P. 706–712.

7) Nakano S.I., Uno T. Efficient generation of rooted trees // National Institute of Informatics:Technical Report: NII-2003-005E.–2003 (July).–P. 1–9.

8) Кручинин В.В. Алгоритмы генерации корневых деревьев на основе процедуры полного разбиения // Прикладная дискретная математика.– 2009.– С. 99–103.

9) Филаретов В.В. Алгоритмы перечисления неизоморфных корневых деревьев на основе лексикографического упорядочения // Синтез, анализ и диагностика электронных цепей: Международ. сб. научн. труд. – С. 108–123.

10) Свирщёва Э.А. Симметрии и построение неизоморфных корневых деревьев // Синтез, анализ и диагностика электронных цепей: Международ. сб. научн. труд. – Ульяновск: УлГТУ, 2016.– С. 124–148.

11) Недорезов М.В, Недорезов П.В., Филаретов В.В. Алгоритм и программа генерации неизоморфных корневых деревьев на основе векторов начальных вершин // Синтез, анализ и диагностика электронных цепей: Международ. сб. научн. труд. – С. 149–162.

12) Недорезов П.В., Филаретов В.В. Применение двоичных кодов для генерации неизоморфных корневых деревьев // Синтез, анализ и диагностика электронных цепей: Международ. сб. научн. труд. . – С. 163–174.

13) Chen I.M., Burdick J.W. Enumerating the non-isomorphic assembly configurations of modular robotic systems // The International Journal of Robotics Research.– 1998.– Vol. 17, no.7.– P. 702–719.

ммулми

Исследовательский проект:

"Обобщение теоремы Пифагора на евклидово пространство размерности n"

Мариевский Никита Андреевич

Муниципальное автономное образовательное учреждение лицей №18 г. Калининград

Малаховский Николай Владиславович, к.ф.-м.н., доцент кафедры гуманитарных наук Калининградского университета управления и экономики филиала Санкт-Петербургского университета управления и экономики

Постановка цели и задач исследования:
Обобщением теоремы Пифагора для трёхмерного евклидова пространства является теорема де Гуа: если тетраэдр имеет прямой угол, то квадрат площади грани, лежащей напротив прямого угла, равен сумме квадратов площадей других трёх граней. В работе рассматривается и доказывается обобщение теоремы Пифагора на случай евклидова пространства n измерений.

Актуальность исследования:
Исследование актуально, поскольку может применяться в теоретической физике (гильбертовое пространство), может найти применение в теории фракталов.

Значимость и новизна исследования:
В узком кругу теорема известна, упоминается в разных источниках, в том числе на английском языке, но в ней чаще всего говорится о площадях, а в данной теореме говорится про «условные объёмы». Для размерности n = 2 это, соответственно, площади. Для размерности n = 3 это объём, для размерности n = 4 это «условный четырёхмерный объём». Новизна же заключается в нестандартном подходе к доказательству теоремы. Доказательство же я считаю кратким, но при этом лаконичным.

Основная часть:

В n-мерном евклидовом пространстве $R^n$ рассматривается ортонормированная система координат с начальной точкой O. Множество n+1 точек $\left\{O, P_i\right\}$ , где $P_i(0, ... , x_i , ... , 0)$ и $x_i>0$ ; образует n-мерный симплекс. Гранями n-мерного симплекса являются (n-1)-мерные симплексы $S_i$ , попарно отогональные друг другу, где $O\notin S_0$ и $P_i\notin S_i$,  Обозначим через $V_i$ объём (n-1)- мерного симплекса $S_i$Справедлива теорема, которая варажается следующей формулой:

$V_0^2 =\sum _{i=1}^n{V}_i^2$ ,  где $V_0$ - объём (n-1)-мерного симплекса образованного точками $P_1, ... , P_n$.

Отдельно рассмотрев правую и левую часть основной формулы, получим:

$\sum _{i=1}^n{V}_i^2=(\frac{1}{(n-1)!}{)}^2 * \sum _{i=1}^n(\frac{1}{x_i^2}*\prod _{j=1}^n{x}_j^2)$

$V_0^2=(\frac{1}{(n-1)!}{)}^2 * \sum _{i=1}^n(\frac{1}{x_i^2}*\prod _{j=1}^n{x}_j^2)$

Совпадение выражений и доказывает теорему.

Список использованной литературы: 

Математика, ее содержание, методы и значение. Под ред. Александрова А.Д., Колмо-горова А.Н., Лаврентьева М.А. М.: Изд. Академии наук СССР, 1956; т.3 - 336 с.
Литцман В. Теорема Пифагора. — М., 1960.
Еленьский Щ. По следам Пифагора. — М., 1961
Клауди Альсина. Секта чисел. Теорема Пифагора. — М.: Де Агостини, 2014. — 152 с. — (Мир математики: в 45 томах, том 5)

Исследовательский проект: "Группы пифагоровых троек."

Советников Тимофей Олегович

Муниципальное автономное образовательное учреждение лицей №18 г. Калининград

Малаховский Николай Владиславович, к.ф.-м.н., доцент кафедры гуманитарных наук Калининградского университета управления и экономики филиала Санкт-Петербургского университета управления и экономики

Цели и задачи:

Работа посвящена созданию группы пифагоровых троек, элементами которых могут являться как действительные, так и комплексные числа, и изучению полученной группы: выделению подгрупп, рассмотрению некоторых свойств. Дальнейшей работой являлось обобщение элементов этих троек на комплекснозначные функции с последующим определением групповых операций на множестве таких троек (элементы которых – функции) и нахождению функций, которые будут удовлетворять этим тройкам.

Актуальность, значимость и новизна:

Понятие группы, а вместе с ним кольца и поля – одни из основных в математике, нахождение этих образов – одна из важнейших задач. Это позволяет систематизировать уже имеющиеся факты и знания, открывать и изучать что-либо новое. Пифагоровы тройки – также очень распространённый математический объект. Создание группы таких троек, а также и их обобщение крайне важны, т.к. систематизируют понятия. Это может помочь в геометрии, в сфере вычислений, особенно компьютерных, а в частности может пригодится в криптографии, т.к. во всех этих сферах применяются пифагоровы тройки.

Краткое описание работы

На множестве $\pi$ пифагоровых троек $A\left[a_1;a_2;a_3\right],B\left[b_1;b_2;b_3\right]$ вводится символическое произведение$*$по закону $A*B\equiv \left[a_1;a_2;a_3\right]*\left[b_1;b_2;b_3\right]=\left[a_1{b}_1+a_2{b}_2;a_1{b}_2+a_2{b}_1;a_3{b}_3\right]$. Элементы $a_i,b_i (i=1,2,3...)$  этих троек могут быть действительными или комплексными числами. Множество пифагоровых троек $\pi$ с введённой операцией $*$ образует коммутативную группу $\pi$, в которой единицей является пифагорова тройка $E\left[1;0;1\right]$, а обратной или инверсной пифагоровой тройкой для произвольной пифагоровой тройки $A\left[a_1;a_2;a_3\right]$ множества $\pi$ является пифагорова тройка $A^{-1}\left[a_1/{a_3}^2;-a_2/{a_3}^2;1/a_3\right]$.

Рассматриваются различные подгруппы группы $\pi$ пифагоровых троек.

1) Группы пифагоровых троек вида $A\left[a;0;a\right],B\left[b;0;b\right]$ 

2) Группы пифагоровых троек вида $A\left[a_1;i{a}_2;a_3\right],B\left[b_1;i{b}_2;b_3\right]$

3) Группы пифагоровых троек вида $A\left[a_1;a_2;1\right],B\left[b_1;b_2;1\right]$.

4) Циклические подгруппы ${\pi }_k$ порядка $k=1,2,3...$ группы $\pi$.

Высказана гипотеза: если разность между первым и вторым элементом тройки $\left[\frac{1}{2}\left(u^2+v^2\right);\frac{1}{2}\left(u^2-v^2\right);uv\right]$ равна 1, тогда все тройки последовательности являются примитивными. Такие тройки образуют последовательность степеней некоторой пифагоровой тройки и, в свою очередь, определяют бесконечную циклическую подгруппу ${\pi }_n$ группы $\pi$. Рассматриваются обобщённые пифагоровы тройки.

5) Обобщённые пифагоровы тройки вида $\left[f_1\left(z_1\right);f_2\left(z_1\right);1\right],\left[f_1\left(z_2\right);f_2\left(z_2\right);1\right], f_1(z_1{)}^2=f_2(z_1{)}^2+1, f_1(z_2{)}^2=f_2(z_2{)}^2+1$.

Групповая операция на множестве этих троек определяется следующим образом$\left[f_1\left(z_1\right);f_2\left(z_1\right);1\right]*\left[f_1\left(z_2\right);f_2\left(z_2\right);1\right]=\left[f_1(z_1+z_2);f_2(z_1+z_2);1\right]$ 

где $f_1(z_1+z_2)=f_1\left(z_1\right)f_1\left(z_2\right)+f_2\left(z_1\right)f_2\left(z_2\right); f_2(z_1+z_2)=f_1\left(z_1\right)f_2\left(z_2\right)+f_2\left(z_1\right)f_1\left(z_2\right)$.

$f_1\left(z\right)=ch\left(z\right), f_2\left(z\right)=sh\left(z\right)$.

6) Обобщённые комплексные пифагоровы тройки вида

$\left[g_1\left(z_1\right);i{g}_2\left(z_1\right);1\right],\left[g_1\left(z_2\right);i{g}_2\left(z_2\right);1\right], g_1(z_1{)}^2=-g_2(z_1{)}^2+1, g_1(z_2{)}^2=-g_2(z_2{)}^2+1$.

Групповая операция на множестве этих троек определяется следующим образом $\left[g_1\left(z_1\right);i{g}_2\left(z_1\right);1\right]*\left[g_1\left(z_2\right);-g_2\left(z_2\right);1\right]=\left[g_1(z_1+z_2);g_2(z_1+z_2);1\right]$

где $g_1(z_1+z_2)=g_1\left(z_1\right)g_1\left(z_2\right)-g_2\left(z_1\right)g_2\left(z_2\right); g_2(z_1+z_2)=g_1\left(z_1\right)g_2\left(z_2\right)+g_2\left(z_1\right)g_1\left(z_2\right)$ .

$g_1\left(z\right)=\cos \left(z\right), g_2\left(z\right)=\sin \left(z\right)$.

Решение поставленных задач опирается на использование основ алгебры и теории функций комплексного переменного.

Итоги исследования

Получен ряд новых результатов, связанных с пифагоровыми тройками чисел и их функциональными обобщениями. Создана группа Пифагоровых троек, произведено обобщение элементов троек на функции. Также высказана гипотеза о нахождении последовательностей примитивных пифагоровых троек. Все это актуально в сфере криптографии, компьютерных вычислений и геометрии.

Список использованной литературы:

1. Курош А. Г. Теория групп. (3-е изд.). М.: Наука, 1967.
2. Холл М. Теория групп. М.: Издательство иностранной литературы, 1962.
3. Малаховский Н.В. Метод комплексных чисел в планиметрии. М.: Издательство Калининградского госуниверситета, 1996.
4. Моденов П.С. Задачи по геометрии. М: Наука, 1979.
5. Скопец З. А.Геометрические миниатюры. — М., 1990 

О некоторых свойствах диагоналей правильного n-угольника

Сизых Артем Константинович,

Калининград, МАОУ лицей №18,

Малаховский Николай Владиславович,

кандидат физико-математических наук, доцент кафедры гуманитарных наук Калининградского института экономики, филиала Санкт-Петербургского университета управления и экономики

Цель: исследовать свойства диагоналей правильных многоугольников, связанные с точками их пересечения.

Постановка задачи: необходимо изучить взаимное расположение точек пересечения диагоналей, а также их число.

Актуальность работы: при изучении правильных многоугольников возникает ряд задач, связанных с пересечением диагоналей правильного многоугольника, также, рассматриваемые в работе многоугольники и их диагонали, можно использовать при проектировании и строительстве зданий необычной формы, в частности зданий, каждый этаж которых представляет собой правильный многоугольник.  

Значимость и новизна исследования: в работе рассматриваются ранее не изученные свойства точек пересечения диагоналей правильного n-угольника.                                               

Методика решения: для решения поставленных задач используются известные формулы комбинаторики, тригонометрии, теории пределов и дифференциального исчисления.

Рассмотрим правильный угольник . Обозначим через $\rho$- радиус, через O- центр описанной около данного n-угольника окружности, а через $d_{\pm k}^i$ диагонали, соединяющие вершину $A_i$ с вершинами $A_{i\pm k}$ . Индекс i равно как и знаки $\pm$ будем опускать в тех случаях, когда индексы вершин, соединённых этими диагоналями не играют роли. Индекс k принимает значения $2\le k\le \left(\frac{n}{2}\right)$ . Через $c_k$ обозначим расстояние от точки O до диагонали $d_k$  n-угольника..

Лемма 1. Расстояние $r_k^p$ от точки пересечения $Q_k^p$ диагоналей $d_{+k }^i и d_{-k}^{i+p}$   до точки  O  определяется формулой $r_k^p=\rho \cos \frac{k\pi }{n} ÷ \cos \frac{(k-p)\pi }{n}$;

Теорема 1. Для любых значений k и $n\ge 4$  $c_{k-1}- r_k^{k-1}>0.$ Для любого значения  k  $\underset{n\to \infty }{\lim }(c_{k-1}-r_k^{k-1})=0.$ Для любых значений k и  $n\ge 4$ $c_{k-1}- r_k^1>-\frac{\rho }{2}.$ В частных случаях для $n\le 11$ величина $c_{k-1}- r_k^1>0$ и предел $\underset{n\to \infty }{\lim }(c_{\frac{n-1}{3}}-r_{\frac{n+2}{3}}^1)=-\frac{\rho }{2}.$

Лемма 2. Число точек пересечения, принадлежащее диагоналям $d_k$ и не принадлежащее диагоналям $d_{k-1},d_{k-2},...,d_2$ равно n(k - 1)(n - 2k).

Теорема 2. Число точек пресечения, принадлежащих всем диагоналям  $d_m$ (m = 2,3,...,k) равно $\frac{n}{6}(k-1)(3kn-4k^2-4k).$

Теорема 3. Вне круга с радиусом  r ( $r_{k+1}^1\le r\le c_k$ ) лежит $\frac{n}{6}(k-1)(3kn-4k^2-4k)$ точек пересечения диагоналей, при $n\ge 11$.

Теорема 4.  При  $n\to \infty$ общее число точек пересечения диагоналей принадлежащих кольцу, ограниченному окружностями с радиусами $\rho$ и $\frac{\rho \sqrt{2}}{2}$ , не меньше половины общего числа точек пересечения всех диагоналей.

Итоги работы: в работе получен ряд новых результатов, связанных с точками пересечения диагоналей правильного - угольника. Полученные результаты обобщаются на случай, когда число сторон правильного многоугольника стремится к бесконечности.

Список литературы:

1) М. Холл Комбинаторика, 1970

2) Аничков Д.С. Теоретическая и практическая геометрия. М., 1870.

3) Архимед. Сочинения. М.: Гос. изд-во физ-мат. литературы, 1962

4) Буняковский В.Я. О правильных многоугольниках, вписанных и описанных около круга // Сочинения В.Я. Буняковского, 1838

Автор работы: Гавриловский Даниил Владимирович, МБОУ «Гимназия№22» г. Белгорода

Научный руководитель: Симаков Михаил Анатольевич,  учитель информатики и ИКТ
муниципального бюджетного общеобразовательного учреждения «Гимназия№22» г. Белгорода

Целью данной исследовательской работы является: разработка программного обеспечения для изучения и визуализации особенностей работы алгоритмов поиска пути.

Задачи: 

• Анализ теоретического по проблеме поиска пути
• Разработка требований к создаваемому программному обеспечению
• Проектирование программного обеспечения
• Реализация программного обеспечения
• Тестирование и отладка созданной программы
• Сбор с помощью созданного программного статистических данных о работе алгоритмов поиска пути

Методы исследования: обзор литературы и анализ информации в сети Интернет, компьютерный эксперимент, SWOT-анализ.

Актуальность работы: задача поиска пути актуальна в таких областях, как робототехника, навигация транспортных средств, разработка игр, индустрия развлечений и т.д. Решение этой проблемы позволит обеспечить автономность функционирования систем, увеличить производительность работы, повысить точность контроля, снизить затраты на подготовительные операции и обслуживание.

Значимость: полученным программным обеспечением можно воспользоваться, чтобы разобраться в тонкостях любого из представленных алгоритмов поиска, смоделировать необходимую ситуацию и принять решение о выборе алгоритма поиска на основе собранной статистики.

Новизна: главными преимуществами нашего проекта являются отображение результата работы сразу нескольких алгоритмов одновременно, возможность сохранять и загружать смоделированные раннее ситуации, возможность создавать отчет для последующей обработки.

Итоги работы: в результате исследования было создано программное обеспечение, позволяющее изучить работу алгоритмов поиска пути. Программа визуализирует процесс работы алгоритмов поиска пути, ведет необходимую статистику и создает файл отчета, готовый для обработки в специально созданных для этого программах. Программное обеспечение имеет механизм моделирования различных ситуаций.

Архив с разработанной программой можно скачать по ссылке: https://www.dropbox.com/s/7s2o702ib45jh2z/

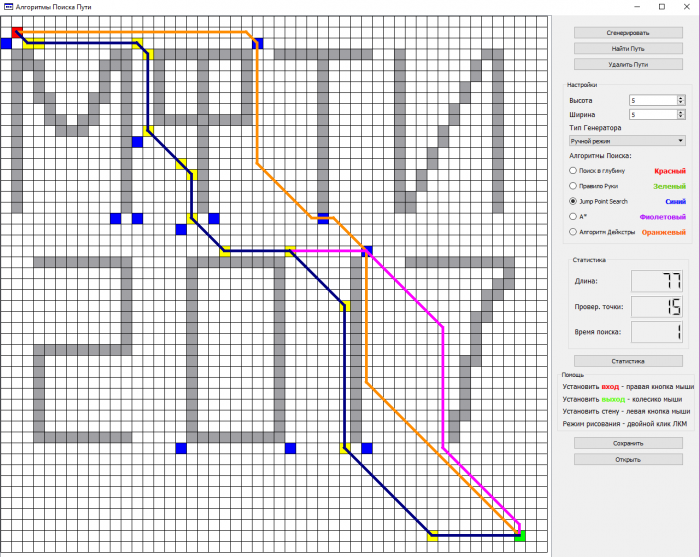
Итерфейс разработанной программы в режиме моделирования

Видео с демонстрацией работы программы

Файл с тезисами: http://abitu.net/conference/1673

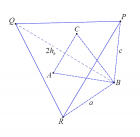
Обратная задача зеркального треугольника

Самолыга Артем Алексеевич,

Калининград, МАОУ лицей №18,

Малаховский Николай Владиславович,

кандидат физико-математических наук, доцент кафедры гуманитарных наук Калининградского института экономики, филиала Санкт-Петербургского университета управления и экономики

Постановка задачи: Вершины произвольного треугольника  (прообраза) симметрируются относительно противолежащих сторон. При этом возникает “зеркальный” треугольник . Определить число всех прообразов по заданному “зеркальному” треугольнику

Методика решения: Решение задачи основывается на известных теоремах тригонометрии, метода координат и использовании свойств конических сечений.  

Актуальность работы: результаты исследовательской работы можно применить в таких областях науки, как кристаллография, минералогия. Так же результаты можно применить в геометрии частиц и расположении их в пространстве.

Значимость и новизна исследования: в работе рассматриваются ранее не изученное свойство “зеркального” треугольника, а именно максимальное количество невырожденных прообразов данного “зеркального” треугольника.

Итоги исследования: Определяются все образы треугольников на плоскости, прообразом которых при симметрировании их вершин относительно противоположных сторон, является заданный треугольник. Доказывается, что из 27 возможных треугольников-образов могут существовать максимально только 7 невырожденных треугольников (причём максимум достигается только в случае равностороннего треугольника-прообраза.

Список литераруры:

1)Моденов П.С. Задачи по геометрии. М: Наука, 1979.
2)Скопец З. А.Геометрические миниатюры. — М., 1990
3)Аничков Д.С. Теоретическая и практическая геометрия. М., 1870.

       Термин «фрактал» стал в последнее время чрезвычайно популярен. Фрактальные объекты изучают математики, ими заинтересовались художники, даже философы. Прежде всего, фракталы - это необыкновенно красиво. Можно часами любоваться причудливыми узорами фрактальных кривых. Математики способны оценить и другую красоту фрактальных объектов - удивительное сочетание тривиальной простоты и запредельной сложности, гармония очевидного и неизвестного. Программистам в этом вопросе будут интересны рекурсивные и итерационные методы, позволяющие выполнить построение причудливых изображений фрактал методы геометрии, широко используемые в естественных науках, основаны на приближенной аппроксимации структуры исследуемого объекта геометрическими фигурами и их композициями, метрические и топологические размерности которых равны между собой. Однако многие природные системы настолько сложны и нерегулярны, что использование только знакомых объектов классической геометрии для их моделирования представляется безнадежным. Речь идет о задачах, для решения которых необходимо учитывать особенности топологии тонкой структуры объектов.

Цель работы: изучить мир фракталов и их применение.

Объект исследования: фракталы.

Актуальность данной темы заключается в том, что фракталы в геометрии, а точнее их наглядность, помогают нам пережить чувства и эмоции, которые мы испытываем.

 Гипотеза: Все, что существует в реальном мире, является фракталом.

Цель, предмет и гипотеза исследования определили постановку следующих задач:

1. Изучить историю возникновения фракталов
2. Узнать виды фракталов
3. Применение фракталов на практике

      Первые идеи фрактальной геометрии возникли в 19 веке. Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками. Пеано нарисовал особый вид линии.

         Само Понятия «фрактал» и «фрактальная геометрия»  были предложены математиком Б. Мандельбротом в 1975 г. для обозначения нерегулярных, но самоподобных структур. Рождение фрактальной геометрии связывают с выходом в 1977 г. книги Б. Мандельброта «Фрактальная геометрия природы», в которой объединены в единую систему научные результаты учёных, работавших в период 1875-1925 гг. в этой области.

           Наука о фракталах очень молода, потому что они стали появляться с развитием компьютерных технологий. Основная причина   применения фракталов в различных науках заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Понятия фрактальной геометрии наглядны и интуитивны. Её формы привлекательны с эстетической точки зрения и имеют разнообразные приложения.  Во всем, что нас окружает, мы часто видим хаос, но на самом деле это не случайность, а идеальная форма, разглядеть которую нам помогают фракталы. Природа — лучший архитектор, идеальный строитель и инженер. Она устроена очень логично, и если где-то мы не видим закономерности, это означает, что ее нужно искать в другом масштабе.

Использование для шифрования текстовой информации квадратной, треугольной и круглой  шифровальной решетки

В работе обосновывается практическая значимость математических знаний о процентах и умений их вычислять для историко-аналитического исследования; представлено удобство использования процентов для сравнительного описания некоторых вопросов.

Работа рассматривает вопросы применения физических излучений для обеззараживания, каких либо объектов, в частности системного блока компьютера. В первой части работы рассматривается природа физических излучений и их воздействие на микроорганизмы. Следующие разделы посвящены изучению бактериальной среды персонального компьютера, и разработке системы бактерицидных излучателей, на основе физических излучений, в составе схемотехники персонального компьютера. Результатом работы явилось создание системы излучателей позволяющей эффективно производить обеззараживание системного блока компьютера. Эксперименты доказали, что система безопасна, как с точки зрения безопасности пользователей компьютером, так и с точки зрения безопасности для самого системного блока. Применение подобной системы излучателей может широко использоваться как в быту, так и в компьютерных классах школ, университетов, вычислительных центрах и других подобных заведениях.

Тезисы к работе: http://abitu.net/conference/1655

ОБ ОДНОМ НЕРАВЕНСТВЕ J. GARFUNKEL И ЕГО АНАЛОГАХ ДЛЯ ДРУГИХ ЗАМЕЧАТЕЛЬНЫХ ТОЧЕК ТРЕУГОЛЬНИКА

Автор:

Орлова Дарья Леонидовна,

ученица 11 класса МБОУ «Гимназия № 40» имени Народного учителя СССР Овсиевской Руфины Серафимовны

Научные руководители:

Мальцев Юрий Николаевич доктор физико-математических наук, профессор Алтайского государственного педагогического университета;

Белоцкая Юлия Николаевна, учитель математики МБОУ «Гимназия № 40» имени Народного учителя СССР Овсиевской Руфины Серафимовны

В журнале Crux Mathematicorum предлагается задача 644 (автор Jack Garfunkel – известный составитель олимпиадных задач по геометрии):

Пусть I – центр вписанной окружности треугольника  и  - точки пересечения прямых  с описанной окружностью (около ).

Доказать, что .

Цель: рассмотреть более общую задачу:

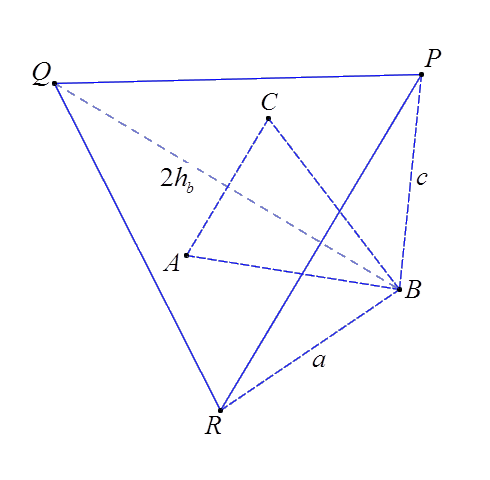
Пусть даны точка P и  и  – точки пересечения прямых  с описанной (около ) окружностью. Найти оценки снизу и сверху, для , когда точка P совпадает с: G, H, I, N. (G – центр тяжести, H – ортоцентр, I – инцентр, N – точка Нагеля) - чертеж приведен в приложении 1.

Представляет интерес гипотеза:

Для любой точки P (внутри ) справедливо .

Актуальность работы заключается в том, что поставленные задачи для классических замечательных точек (G, H, I, N) интересны для специалистов по элементарной геометрии.

Научная новизна: полученные результаты являются новыми и ранее не встречались в известной нам литературе.

Основные результаты:

Теорема 1. Пусть I – инцентр  и  – точки пересечения прямых  с описанной (около ) окружностью. Тогда:

• ;
• Справедлива оценка снизу: .
• Справедлива оценка сверху: , где .

При этом неравенства во втором и третьем утверждении превращаются в равенства тогда и только тогда, когда  правильный и .

Теорема 2. Пусть точка G – центр тяжести  и  – точки пересечения прямых  с описанной (около ) окружностью, тогда справедливо равенство

.

Теорема 3. Пусть H – ортоцентр остроугольного  и  – точки пересечения  с описанной (около ) окружностью. Тогда:

Теорема 4. Пусть N – точка Нагеля  и  – точки пересечения  с описанной (около ) окружностью. Тогда:

 и может оказаться меньшим 3.

Таким образом:

• В работе по-новому решена задача Джека Гарфанкеля (теорема 1). Найдены оценки снизу и сверху для .
• Выдвинутая гипотеза верна для G и H (теорема 2, 3) и опровергнута для N (в приложении приведен контрпример).

Список использованной литературы

• Зетель С.И. Новая геометрия треугольника, Москва, Учпедгиз, 1962 г.
• Мальцев Ю.Н. «Реши + Если = Силен», Избранные лекции по математике, издательство АлтГУ, Барнаул, 2002 г.
• Солтан В.П., Мейдман С.И. «Тождества и неравенства в треугольнике». Кишинев: Изд-во Штиинца, 1982.

Gurfunkel J. Problem 644. // Crux Mathematicorum. – 2007. – v. 22. – p.22.

Актуальность: полученные при исследовании целочисленных треугольников результаты будут интересны как специалистам в области элементарной геометрии, так и учащимся выпускных классов при поиске нестандартных способов и методов решения задач, связанных с теорией целых чисел, в том числе при решении задач группы С на ЕГЭ.

Цель работы: предложить способ перечисления всех возможных целочисленных треугольников, в которых один из углов является рациональной частью развернутого, т.е. равен ∙180, где m и n– целые числа (особые треугольники).

Задачи:

1. Путем решения диофантовых уравнений найти возможные значения сторон особых треугольников.
2. Разработать компьютерную программу для нахождения всех троек целых чисел, являющихся сторонами особых треугольников.

Объект: треугольники

Предмет: особые треугольники

Основная теорема исследования: треугольник с целочисленными сторонами может иметь один из углов равный рациональной доле развернутого, т.е. быть особым, в том и только том случае, когда его угол равен 60, 90 или 120 градусов.

Так как данная теорема не даёт механизма при котором удалось бы получить конкретные примеры треугольников с конкретными сторонами или доказать, что таких треугольников не существует, были отдельно рассмотрены три вида треугольников с углами: 60°,90°,120°.

Для каждого из них на основе теоремы косинусов составлено и решено диофантово уравнение и используя его решения, составлена программа, приведенная в приложении 1, а результаты представлены в приложении 2.

Таким образом, в ходе исследования удалось найти необходимые и достаточные условия, чтобы тройки целых чисел (а, в, с) являлись бы длинами сторон какого-нибудь особого треугольника и составить программу для нахождения корней диофантовых уравнений.

Список использованной литературы и интернет-ресурсы.

1. Виленкин Н.Я. и др. Алгебра и математический анализ для 10 класса М: Просвящение, 1995-335с.
2. Туманов С. И. Поиски решения задачи, изд. Просвещение, 1969-280с.
3. .Шклярский Д.О. Часть 1 Арифметика и алгебра. Избранные задачи и теоремы элементарной математики. Государственное издательство физико-математической литературы. 1968-311с.
4. Keith Selkirk The Mathematical Gazette Integer-Sided Triangles with an Angle of 120°

МБОУ «Брянский городской лицей №2 имени М.В.Ломоносова»

Научно-исследовательская работа «Транспортная задача»

Автор: ученик 11^б класса Карамушко Денис     Научный руководитель: Воронцова Е.В.

 Математическое моделирование играет большую роль в решении различных экономических проблем, позволяя определить цели и типы их решения, обеспечивая структуру для целостного анализа. Частью математического программирования являются транспортные задачи, которые играют особую роль в уменьшении транспортных издержек предприятия. Это является актуальным вопросом в условиях рыночной экономики, когда любые затраты должны быть минимизированы.

Классическая «транспортная задача» – задача о наиболее экономном плане перевозок однородного продукта из пунктов производства в пункты потребления. Целью решения транспортной задачи является разработка наиболее рациональных путей и способов транспортировки товаров, устранение чрезмерно дальних встречных и повторных перевозок.

Уже после того, как я увлекся изучением различных математических методов решения транспортных задач, возникла ситуация, в которой я получил возможность использовать математическое планирование на практике. Перед Новым годом благотворительный союз «Друзья детей Брянска» осуществлял развозку подарков от нескольких складов к разным социальным учреждениям.

Гипотеза: при помощи методов математического планирования можно значительно (до 5%) сократить транспортные расходы на доставку новогодних подарков детям.

Цель работы: рассчитать оптимальный маршрут доставки новогодних подарков детям, попавшим в трудные жизненные ситуации, используя методы решения транспортной задачи.

Объект исследования: маршрут доставки новогодних подарков детям, попавшим в трудную жизненную ситуацию.

Предмет исследования: оптимизация маршрута с помощью различных методов решения транспортной задачи.

Задачи:

1. Изучить методы решения транспортной задачи (на примере решения абстрактных задач).
2. Составить условие транспортной задачи (подготовить и рассчитать необходимые данные).
3. Выбрать наиболее целесообразный метод (или комбинацию методов) для решения задачи о доставке подарков.
4. Решить задачу о доставке подарков.
5. Использовать решение задачи на практике.
6. Оценить экономию при использования оптимального плана перевозки
7. Проанализировать полученные результаты.

Проведенное исследование подтвердило гипотезу о том, что при помощи методов математического планирования можно значительно (до 11% (!)) снизить стоимость перевозки. Союз «Друзья детей Брянска» благодарен за проделанную работу.

Список использованной литературы:

1. Галяутдинов Р.Р. Транспортная задача - решение методом потенциалов // Сайт преподавателя экономики. – http://galyautdinov.ru/post/transportnaya-zadacha
2. Замотайлова Д.А. Оптимизация перевозок с использованием автоматизированной информационной системы визуального решения транспортных задач/Д.А. Замотайлова // Научный журнал КубГАУ. – 2010. - №60(06) – с.1-4
3. Решение транспортной задачи онлайн. – http://math.semestr.ru/transp/index.php
4. Самаров К.Л. Учебно-методическое пособие по разделу «Транспортная задача» / К.Л. Самаров. – М.: Резольвента, 2009. – 23 с.
5. Транспортная задача // Википедия – свободная энциклопедия. – https://ru.wikipedia.org/wiki/Транспортная_задача
6. Транспортная задача // Корпоративный портал Томского политехнического университета: http://portal.tpu.ru
7. Триус Е.Б. Задачи математического программирования транспортного типа / Е.Б. Триус. – М.: Советское радио, 1967. – 209 с.

Выполнил: Лязгина Настя, 5 класс МОБУ Лицей № 6 г. Мелеуза

Научный руководитель: Шагалеев М.М., учитель информатики

Моя семья живет на 6-ом этаже в 9-ти этажном доме. А мне очень хочется жить в своем доме, чтобы вышел из дверей и уже на улице. Пока у нашей семьи нет возможномти переехать с свой дом и я решила построить сама свой дом мечты.

Я поставила цель: построить дом мечты. 

В ходе исследования я хочу изучить: архитектуру города Мелеуза, этапы постойки дома, 3Д модели дома.

Проводя исследование, я использовала различные методы исследования: анализ публикаций и материалов интернета по донной теме, опрос, практические опыты, обобщение.

Конечно, сначала, мне нужнобыло узнать, что же такое архитектураю Словарь Ожегова дает три определения слова АРХИТЕКТУРА: искусство проектирования зданий и сооружений, стиль постройки, здбания и сооружения.

в первую очередь, мы пошли в краеведческий музей г. Мелеуза. Там узнали много интересного: историю г. Мелеуза и строительства зданий, когда построены первые здания и какие из них сохранились.

Далее я сделала поэтажный проект дома.

Потом начался самый интересный этап: постройка дома. Из набора кирпичиков у меня получился трехэтажный дом.

А потом я задумалась, ведь сейчас век компьтеров, и, наверное, архитекторы уже не чертят проекты на бумаге. Мы нашли программу для создания проектов домов SweetHome 3D.

Изучив эту программу, я создала проект нащего дома. Меня очень увлек процесс "строительства" в программе: я возводила стены, раскрашивала их в нужный цвет, расставляла мебель и другие предметы интерьера. Но мне не хватило, имеющихся в программе, предметов. Мы скачали недостающие из интернета. Так, у меня во дворе поселилась собака и выросло дерево, дома появились кошки, цветы и многое другое.

Делай проект, я построила модель дома своей мечты. Мне удалось узнать много интересного о домах моего города, и теперь я смотрю на них другими глазами.

Я думаю, мой проект будет полезен и учителям для ознакомления школьников, и тем, кто захочет жить в таком доме, ну и, конечно, мне.

Мне очень понравилось строить дом. Я думаю, при выборе будущей профессии, одним из вариантов может быть, профессия архитектора.

А закончить свой проект, я хотела бы отрывком из стихотворения Юрия Гребенева:

Я хочу простроить дом.. И его построю!

Все мечты свои о нем воплощу, раскрою,

Доброту, тепло, любовь по Земле рассею,

И вздохнет свободно вновь юная Россия!!! 

      В работе исследовано однопараметрическое семейство траекторий движения точек треугольника Рёло, расположенных на его оси симметрии, при качении его по квадрату. Найдены все бифуркационные значения, при прохождении через которые качественно меняется форма траектории. Установлены компоненты из которых состоят траектории, определено их количество и уравнения. При всех значениях параметра, превышающих первое бифуркационное значение, рассчитано отношение площади фигуры, ограниченной замкнутой кривой, к площади описанного вокруг фигуры квадрата. Найдено лучшее приближение к квадрату. Все расчеты сделаны точно, без применения приближенных вычислений. Результаты данного исследования позволяют сделать механизм, способный высверливать квадратные отверстия с высокой точностью. С его помощью можно получать углы с точностью в 0,07%. Такой процесс может составить конкуренцию лазерной резке.

Исследовательский проект: «Аффинный аналог теоремы Наполеона»

Кормилицина Александра

Муниципальное автономное образовательное учреждение лицей №18 г. Калининград

Научный руководитель: Малаховский Николай Владиславович, к.ф.-м.н., доцент кафедры гуманитарных наук Калининградского университета управления и экономики филиала Санкт-Петербургского университета управления и экономики

Постановка задачи:

Классическая теорема Наполеона формулируется следующим образом: если на сторонах невырожденного треугольника как на основаниях построены правильные треугольники, не имеющие с данным треугольником общих внутренних точек, то центры построенных треугольников образуют правильный треугольник. Заметим, что теорема останется в силе, если правильные треугольники строить как во внешнюю, так и во внутреннюю стороны данного треугольника, причём центр тяжести равностороннего треугольника совпадает с центром тяжести данного треугольника. Поставим вопрос о нахождении выпуклых n-угольников, обладающих свойствами, аналогичными сформулированным в классической теореме Наполеона.

Методика решения:

Решение поставленной задачи будем осуществлять методом комплексных чисел в планиметрии, отождествляя комплексные числа с точками на плоскости комплексных чисел.   

Актуальность, значимость и новизна исследования:

Используя наклонное преобразование плоскости, доказывается обобщённая теорема Наполеона, что используется в аффинной геометрии.

Итоги исследования:

Введено понятие наклонного преобразования $\theta$ плоскости, являющегося частным случаем аффинного преобразования плоскости. Используя наклонное преобразование плоскости, доказывается обобщённая теорема Наполеона: если на сторонах аффинно-правильного n- угольника построены правильные n - угольники (все во внешнюю или все во внутреннюю сторону), то их центры образуют правильный n- угольник. Рассматривается предельный случай теоремы при $n\to \infty$. Определяются конечные радиусы окружностей - центров правильных  - угольников в случае, когда $n\to \infty$. Находится связь между полуосями эллипса, являющегося образом окружности при наклонном преобразовании $\theta$ плоскости и определяющими это преобразование углом поворота $\phi \left(\phi \ne \pi /2 + \mathrm{\pi k}, k\in \mathbb{Z}\right)$ и действительным положительным числом $\lambda$ - коэффициентом растяжения-сжатия.

Список использованной литературы:

1. Малаховский Н.В. Метод комплексных чисел в планиметрии. М.: Издательство Калининградского госуниверситета, 1996.
2. Моденов П.С. Задачи по геометрии. М: Наука, 1979.
3. Скопец З. А.Геометрические миниатюры. — М., 1990 

Автор: Ахмедов Исак Азизович, Республика Дагестан, г. Махачкала,

МБОУ «Лицей № 8», 10 ф/т  класс

Научный руководитель: Хаиров Рагим Айдабекович,  г. Махачкала, Дагестанский государственный аграрный университет, кафедра высшей математики, старший преподаватель.

Многочлены Чебышева первого и второго рода 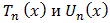определены через косинус, синус и арккосинус. Аналогично определены и функции  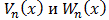через косинус, синус и арксинус:

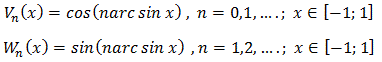
В литературе для этих функций приведены определения и соотношения связи с многочленами Чебышева в случаях четных и нечетных номеров.

В нашей работе для тех же функций получены:

• формулы, выражающие указанные функции через многочлены Чебышева, и наоборот;
• формулы и некоторые свойства нулей;
• рекуррентные соотношения, с помощью которых установлены некоторые свойства рассматриваемых функций.

Литература:

1. Суетин П.К. Классические ортогональные многочлены. – М.: Физматлит, 2007-480с.
2. Кампе де Ферье, Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики – М.: Физматлит, 1963-102с.

Геометрия на клетчатой бумаге

Автор работы: Пителина Ксения Владимировна, 6 класс МОУ «Лицей №7» г. Саранск

Руководитель: Леонова Татьяна Ивановна, учитель математики МОУ «Лицей №7»

Цель работы: рассмотреть различные методы решения задач на клетчатой бумаге.  

Задачи исследования:

• изучить литературу, в поисках различных методов и приёмов решения задач на клетчатой бумаге;

• систематизировать исследуемые задачи;
• научиться выполнять построения, используя «узлы» квадратной сетки;
• использовать полученные знания для решения нестандартных задач.

Актуальность: занятия геометрией на клетчатой бумаге создают условия для успешного усвоения геометрического материала. Задачи на клетчатой бумаге способствуют развитию интуиции, воображения, внимания, что необходимо в подготовке к математическим олимпиадам.

Новизна исследования состоит в классификации задач на клетчатой бумаге.

Обычно для занятий геометрией нужно приготовить много  канцелярских принадлежностей: бумагу, карандаш, линейку с делениями, циркуль, транспортир... Оказывается, множество интересных задач можно решать, имея всего лишь линейку без делений, листок клетчатой бумаги и карандаш!

Предлагаемые задачи по большей части выбраны из различных олимпиад и придуманы серьёзными авторами. Всё это говорит о том, что геометрические задачи на клетчатой бумаге достойны отдельного разговора.

В ходе выполнения работы мы пришли к выводу – решение задач на клетчатой бумаге в большей степени, чем решение обычных задач, помогают:

• развивать геометрические представления,
• вырабатывают необходимые вычислительные навыки,
• формируют практические умения при построении геометрических фигур,
• подготовиться к экзаменам и участию в олимпиадах по математике.

Список использованных источников

1. Блинков А. Задачи на решетке.// Квантик. №9. – 2015. – С. 10-14.
2. Васильев Н.Б., Егоров А.А. Задачи всесоюзных математических олимпиад/ Н.Б. Васильев, А.А. Егоров – М: Наука. – 1988. – 288 с.
3. Горина Л.В. Одна за всех… Формула Пика.// Математика. Все для учителя. №3. – 2013. – С. 24-28.
4. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика. 6 класс: учеб. для общеобразоват. учреждений. «МГУ-школе»/ С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин – М.: Просвещение. – 2012. – 259 с.

Создание единой системы мониторинга ("Умной диспетчерской") - системы слежения за сигналами датчиков электронных систем "Умного города" на основе 3-d модели. Модель города разработана в MaxonCinema 4DStudioR16. Обработка сигналов реализована с помощью сети светодиодов, соединённых в электрическую сеть, проложенную через здания макета города. Для автоматизации модели использован Arduino MEGA 2560.
Подробно о ходе работы и результатах в приложенном файле.

Исследовательский проект: "Методы решения задач на графах при помощи производящих функций"

Первеев Михаил

МАУ ДО ЦДО "Стратегия" и МБОУ СОШ №2 г.Липецка

Шуйкова Инесса Анатольевна, к.т.н., доц. кафедры прикладной математики ЛГТУ

Цель работы: углубленное изучение производящих функций и решение некоторых задач на графах при помощи аппарата производящих функций.

Методы, используемые в работе: в работе используются методы комбинаторики для анализа исследуемых объектов, начальные знания по теории графов, а также аппарат производящих функций.

Актуальность работы: теория производящих функций позволяет решать такого рода задачи компактно, лаконично, используя красивый и убедительный математический аппарат. При помощи аппарата производящих функций можно решать как базовые, так и достаточно сложные задачи на графах.

Описание научно-исследовательской работы: исследовательская работа является продолжением практического исследования, начатого автором в 9 классе. Первый год работы был посвящён изучению основных комбинаторных объектов, рекуррентных соотношений, позволяющих подсчитывать количество этих объектов и производящих функций для числовых последовательностей. Были изучены методы, позволяющие решать рекуррентные линейные рекуррентные соотношения. Были рассмотрены и решены различными способами некоторые комбинаторные задачи, такие как задача Фибоначчи, задача “Размен” и “Счастливые билеты”. Также была реализована компьютерная программа, позволяющая генерировать комбинаторные объекты.

Темой продолжения исследования в текущем году стали методы решения задач на графах при помощи производящих функций. Были более подробно изучены производящие функции. Рассмотрены некоторые задачи на подсчёт количества путей в графах, такие как “Пути шахматным королём”. Изучены правильные скобочные последовательности, их связь с путями Дика, а также способы подсчёта их количества. Реализованы компьютерные программы, позволяющие решать задачу о шахматном короле и генерировать путь Дика и дерево по заданной правильной скобочной последовательности.

Выводы: в ходе исследования были поставлены и решены следующие задачи: изучена литература по исследуемой теме, продолжено изучение аппарата производящих функций, решены некоторые задачи на графах при помощи иссследуемого аппарата, созданы компьютерные программы, решающие рассмотренные задачи. Планируется более углубленное изучение производящих функций и решение более сложных задач с их помощью.

Библиографический список:

1. Виленкин Н.Я. Популярная комбинаторика. – М.: “Наука”, 1975.
2. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики. – М.: “Мир”, 1998.
3. Костюкова Н.И. Основы информационных технологий. Графы и их применение. Комбинаторные алгоритмы для программистов. – М.: “БИНОМ. Лаборатория знаний”, 2007.
4. Ландо С.К. Введение в дискретную математику. – М.: МЦНМО, 2012.
5. Сайт алгоритмов и программ [Электронный ресурс] // MAXimal. URL: http://e-maxx.ru/
6. Сайт о производящих функциях последовательностей [Электронный ресурс] // Производящие функции 2010. URL: http://genfunc.ru/

Создание реберных конструкций правильных многогранников с помощью пластиковых жёстких трубочек. Разработка правил сборки и расчёт длины лески для моделирования.

тезисы

     В книге [1] поставлена такая задача: исследовать количество корней уравнения  в зависимости от a, b, c; изобразить соответствующие области в пространстве параметров  (a, b, c). Цель нашей работы – привести уравнение четвертой степени к виду, содержащему два коэффициента, и изобразить на плоскости этих коэффициентов области, в которых уравнение имеет данное количество действительных корней.

     Уравнение  линейной заменой неизвестной сводится к одному из трех видов: ; ; , где коэффициенты p, q выражаются через коэффициенты a₀, a₁, a₂, a₃, a₄ исходного уравнения. Для каждого из них на плоскости (p, q) указаны области, где уравнение имеет данное количество решений. Поставленная цель достигнута.

«Литература»

Сгибнев А.Н.  Исследовательские задачи для начинающих. – М.: МЦНМО, 2013.

ИГРА С ЧИСЛАМИ

(ВСЛЕД ЗА РАМАНУДЖАНОМ)

Махиня Данила Алексеевич

Научный руководитель: Супрягина Ирина Ивановна

 Санкт-Петербург.

Изучение чисел и их свойств-одна из самых интересных и завораживающих тем в математике. Когда ты видишь интересную последовательность бесконечных радикалов или формулу, которая обладает своеобразной математической красотой, то хочется приобщиться к этому интересному миру чисел, понять как это работает, разгадать закономерность. В данная работе происходит знакомство читателя с научными изысканиями таких математиков как: Поль Адриен Морис Дирак, Сриниваса Рамануджан Айенгор,-а также исследование их формул. Показывается пример анализа формул этих математиков и вывода новых последовательностей на основе этого анализа.

Исследовательская работа включает в себя:

1.Знакомство с Рамануджаном.

2.Доказательство некоторых известных формул и их анализ.

3.Вывод собственных формул на основе знаний, полученных из доказательств формул известных математиков.

В ходе работы я научился анализировать формулы. Мне удалось исследовать и доказать несколько формул известных математиков, также я вывел несколько своих формул и последовательностей

В практической деятельности человека часто возникают задачи на поиск траектории движения некоторого объекта...

Тезисы

«Нейрокриптография и нейрокриптоанализ. Реализация протокола синхронизации ключей двух абонентов на базе нейронных сетей и его применение»

Автор:  Плотников Егор Андреевич, Республика Марий Эл, г. Йошкар-Ола, ГБОУ РМЭ “Политехнический лицей-интернат”

Научный руководитель: Кожанова Анна Михайловна, учитель информатики.

Цель:  Показать возможность применения нейрокриптографии в реальных проектах. Создать реализацию алгоритма на базе нейронных сетей для синхронизации закрытого ключа у двух абонентов, используя открытый канал связи.

Задачи: изучить возможность применения нейронных сетей в криптографии для реальных проектов, создать кросс-платформенную реализацию библиотеки, включить в неё весь необходимый функционал, поделиться результатами работы с open-source сообществом.

Методы исследования: для разработки проекта использовался ресурс GitHub (ссылка на репозиторий проекта: https://github.com/egorplotnikov/NeuralCryptography ). Сейчас разработка ведется на языке C# (платформа mono, операционная система GNU/Linux), в дальнейшем планируется написать ещё две версии на языках Java и C++.

Актуальность: 

С каждым годом компьютерная информация играет все более важную роль в нашей жизни, и все большую актуальность приобретают проблемы ее защиты.

Защита от каждого типа опасности предполагает собственные решения. Впрочем, есть и универсальные подходы, способные обезопасить данные от разных угроз. Одним из них является нейрокриптография - раздел криптографии, изучающий применение стохастических алгоритмов, в частности, нейронных сетей, для шифрования и криптоанализа. В данном проекте реализован протокол синхронизации закрытых ключей на базе нейронных сетей  для иллюстрации практического применения  подобной технологии в коммерческих проектах.

Значимость и новизна:

Данная работа призвана показать новые пути для развития информационной безопасности благодаря нейрокриптографии. Эта область достаточно молода, и пока не имеет практических применений. Однако уже сейчас она может использоваться там, где есть непрерывная генерация ключей.

Также эта работа призвана решить ряд проблем, возникающих в классическом варианте реализации, предложенном В.Кинцелем и И.Кантером.

Итоги: в результате был создан первый рабочий образец, способный наглядно показать процесс синхронизации и произвести некоторые оценки, также были разработаны и реализованы варианты решения проблем классической версии алгоритма и заданы векторы дальнейшего развития. Проект находится в стадии активного развития, и любой желающий может принять в нем участие (сейчас все исходные коды доступны на GitHub-е и распространяются под лицензией MIT).

Была проделана большая работа, связанная с изучением англоязычного материала, что помогло автору решить поставленные задачи.

Список литературы:

 "Analysis of Neural Cryptography" by Alexander Klimov, Anton Mityaguine, and Adi Shamir.

 "Permutation Parity Machines for Neural Synchronization" Oscar Mauricio Reyes; Ingo Kopitzke & Karl-Heinz Zimmermann. 

"Successful attack on permutation-parity-machine-based neural cryptography" Luís F. Seoane & Andreas Ruttor. 

"Genetic attack on neural cryptography" Andreas Ruttor; Wolfgang Kinzel;

“Защита  информации  в  компьютерных системах и сетях” Романец,  Ю.  В. 

“Прикладная   криптография.   Протоколы, алгоритмы, исходные тексты на языке СИ” Шнайер   Б.  

Область исследования: имитационное моделирование экологических процессов, среда программирования NetLogo.

Цель проекта: Построить имитационную модель динамики количества деревьев в искусственной среде. Разработать компьютерную модель. Исследовать поведение системы при различных входных параметрах.

Ключевые слова: экология, имитационное моделирование, Netlogo.

Проблема сохранение лесного массива на планете в достаточном количестве является одной из важнейших задач, стоящих перед человечеством в современном мире.  Леса являются основным источником кислорода и потребителем углекислого газа на нашей планете, средой обитания огромного числа микроорганизмов, грибов, растений и животных.  Леса оказывают серьезное влияние на климат Земли.  Жизнь человека с древнейшей эпохи неразрывно связана с лесом, без достаточного количества лесов невозможна сохранность экосистем на планете, а значит и жизни на Земле в том виде в, каком мы его сейчас наблюдаем.

Бесконтрольная вырубка лесов представляет угрозу для атмосферы и жизни человека в целом. Ежегодно вырубается около 95 миллионов деревьев по всей планете. Кажется, что деревьев достаточно много, но на самом деле это далеко не так.

Возникает вопрос: «Сколько надо посадить деревьев, чтобы количество деревьев росло, а не уменьшалось?» Имитационное моделирование может помочь дать ответ на этот вопрос.

В данной работе предлагается имитационная модель демонстрирующая влияние человека на количество деревьев.

Общие положения

Пусть в двумерном пространстве задается совокупность агентов двух типов: людей и деревьев. Первоначально количество деревьев и людей задается произвольно. Считаем, что количество деревьев меняется в зависимости от количества людей. Пусть Х количество людей, а Y – количество деревьев в момент времени T. Каждый такт времени каждый человек срубает k деревьев и сажает m деревьев. T. e. количество деревьев в следующий такт можно рассчитать по формуле (1):

X[T+1] = X[T] – k ∙Y[T] + m ∙Y[T]     (1)

Дерево характеризуется своим возрастом. Известно, что для того чтобы использовать деревья их возраст должен быть выше некоторой величины. Будем называть такие деревья взрослыми. Обозначим ее в модели переменной Time. Считаем также, что у агентов есть ресурс R. Ресурс агента каждый такт времени увеличивается на единицу если вокруг него есть взрослые деревья, и уменьшается на единицу в противном случае.  При моделировании полагалось также, что дерево живет определенное количество лет (200 лет).  Агенты люди каждый такт времени делают один шаг в случайном направлении.

В каждой точке двумерного мира может расти произвольное количество деревьев и находиться произвольное количество людей. Т.е. точка может представлять собой какой-нибудь большой участок земли. 

Если ресурс агента становится больше 20 единиц, то он делится. При делении агент теряет половину своего ресурса.  С помощью этого мы можем проверить насколько комфортно людям существовать в мире. Т.е. если деревьев много, то население растет, и наоборот в противном случае.

При работе над проектом проведена серия компьютерных экспериментов и получены следующие результаты.

Если человек сажает меньше деревьев, чем вырубает, то очевидно, что в скором времени все агенты погибнуть, что и показывает поведение модели. На 99 момент времени в мире остается всего два человека. Второй случай: если человек сажает столько же деревьев сколько вырубает, то численность деревьев постоянная. Количество деревьев, людей и энергия колеблются на одном уровне. В третьем случае, если человек сажает 5 деревьев вместо 2-х вырубленных, то мы наблюдаем положительную динамику. Количество деревьев, людей, взрослых деревьев и энергия растут. Третий случай представлен на рис. 1.

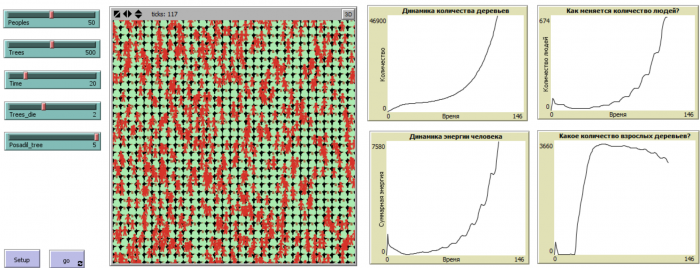
Рис. 1. Результаты компьютерного эксперимента в среде NetLogo.

Выводы

Таким образом построена имитационная компьютерная модель. Продемонстрирована работоспособность модели. Проведено компьютерное исследование модели.

Литература

1. http://www.geo.ru/ekologiya/skolko-v-lesu-derevev
2. http://wood-prom.ru/clauses/spravochnye-dannye/skolko-derevev-na-zemle
3. https://ru.wikipedia.org/wiki
4. К. Н. Мезанцев. Мультиагентное моделирование в среде NetLogo, «Лань», 2015 г.

В любой организации существует необходимость оперативно реагировать на различного рода события. Обычно для этого люди создают объявления на сайтах, звонят или пишут сообщения. BlueBoard дает возможность быстро и эффективно распространить любое объявление для определенного круга пользователей. Система делового общения BlueBoard позволяет реализовать эффективное и быстрое общение среди сотрудников. Будь то необходимость анонсировать важное мероприятие или распределить задачи.

Развитие новых информационных технологий позволяет сделать процесс бесплатного, виртуального обучения города реальным. Но в настоящее время, для Челябинска таких возможностей нет.

Актуальной становится проблема отсутствия бесплатных приложений - путеводителей по городу Челябинск

Целью работы: Написать приложение-путеводитель для Android, позволяющее легко изучить город и получить дополнительную информацию по объектам достояния Челябинска.

Для достижения данной цели нужно выполнить следующие задачи:

• Провести анализ рынка
• Посмотреть на готовые решения
• Провести опрос
• Составить алгоритм
• Приготовить разметку
• Написать парсер и переводчик JSON
• Написать адаптер ListView
• Протестировать приложение
• Составить зеленую линию и наполнить приложение
• Выложить приложение в Play Market

Объектом исследования является разработка приложений на Android. Предметом исследования: среда разработки Android Studio.

В ходе разработки было использована библиотека Picasso для загрузки изображений из интернета.

В будущем планируется добавить поддержку нескольких маршрутов.

Разработка имитационной модели стратегического вооружения высокой точности с использованием алгоритмов оптимального целераспределения и вероятностных алгоритмов, принципов баллистики и алгоритмов построения распределенных систем.

Значимость исследования:

С каждым годом популярность компьютерных игр растет, все больше и больше людей играют в компьютерные игры. Результатом технологического развития, а также массового распространения персональных компьютеров, планшетов и мобильных устройств, стал все более расширяющийся рынок развлечений, что является веским аргументом в пользу проектов по созданию новых игр.

Актуальность разработки игр становится все более неоспоримой,  рынок игр увеличивается в геометрической прогрессии. Самые удачные проекты продаются миллионными тиражами. Зарождение игровой индустрии началось в 1970-х годах одновременно с продажей первых компьютеров, рассчитанных на массового потребителя. За 40 с небольшим лет индустрия компьютерных игр развилась до таких масштабов, что уже во многом опережает своих ближайших конкурентов: киноиндустрию, музыкальную индустрию, шоу-бизнес.

Многие разработчики рассматривают индустрию компьютерных игр лишь как сектор экономики, в котором можно неплохо заработать. Но, на самом деле, создание игр это ещё и инструмент культуры.

Ретро игры были придуманы много лет назад, но и сейчас они пользуются большой востребованностью. Яркий пример - Mario, серия компьютерных аркад, в которые с удовольствием играют пользователи нескольких поколений. Но наверное, она бы не была такой популярной, если бы не имела развитие. Super Mario Maker - игра, в которой игрок имеет возможность не только проходить уровни, но и создавать свои собственные.

На сегодняшний день возрождение старых игр может являться актуальным и выгодным проектом.

Объект исследования: компьютерная игра в жанре аркада.

Предмет исследования: инструменты разработки и программированиекомпьютерной игры в жанре аркада.

Цель: создание компьютерной игры.

Задачи:

• выбор инструментального программного обеспечения;
• проектирование игрового процесса игры;
• проектирование интерфейса
• разработка аркадной игры на основе принципов игры "Змейка" с расширением гемплея и возможностей игры.

Системные требования:

1. ПакетVisualC++ дляVisualStudio 2012. Данный пакет можно скачать бесплатно на официальном сайте Microsoft. Ссылка для скачивания пакета: http://www.microsoft.com/ru-ru/download/details.aspx?id=30679
2. Операционная системаWindows.
3. 50 Mb оперативной памяти.
4. Клавиатура, компьютерная мышь.

Мое исследование началось с решения задачи о сумме углов пятиконечной звезды. Результат показался мне интересным и я попробовала рассмотреть другие звездчатые многоугольники, которые в своей работе я называю звездами. Мне удалось произвести классифицикацию звезд, выяснить их свойства.

В работе сформулировано определение звезды  к-го порядка, выведена формула суммы углов n-конечной звезды к-го порядка, дано определение правильной звезды к-го порядка и рассмотрены свойства правильных звезд.

В своей исследовательской работе литературой и другими источниками я не пользовалась.

Анализ сайтов на наличие Sql – инъекций

Автор: Шарков Леонид Николаевич, МБОУ «лицей №11 г.Челябинска», класс 11

Научный руководитель: Хохлов Алексей Сергеевич, учитель информатики, руководитель учебно-консультационного пункта информатизации МБОУ «лицей №11 г.Челябинска»

Самыми распространёнными уязвимостями, позволяющими получить доступ к базам данным сайта являются sql-инъекции. Существующее программное обеспечение, анализирующее url на возможность применения инъекций, не позволяет в полном объёме проверить все ссылки сайта на уязвимость.

Цель работы: написать программу, которая позволяла бы проверить определённый сайт полностью на возможность внедрения sql-инъекции.

Для достижения поставленной цели необходимо решить следующие задачи:

• Создание рационального алгоритма для парсинга ссылок, принадлежащих определённому домену.
• Изучение готовых программ и материалов по sql-инъекциям.
• Написание программы, которая должна искать ссылки, расположенные на определённом сайте, и их анализировать на возможность применения sql-инъекции.
• Анализ эффективности программы.

Определение. Внедрение Sql-кода (Sql-injection) – один из распространённых способов взлома сайтов или программ путём внедрения произвольного sql-кода, основанный на некорректной обработке входных данных.

Принцип атаки sql-инъекцией:

Допустим программа, расположенная на сервере, выполняет такой PHP-код:

…
$id = $_REQUEST['id'];
$res = mysql_query("SELECT * FROM news WHERE id_news =".$id);
…

Если место ожидаемого числового значения id (например https://site.com/index.php?id=5), программа получает запрос, содержащий конструкцию sql-кода (например https://site.com/index.php?id=-1+OR+1=1), то скриптом выполнится следующий запрос:

SELECT * FROM news WHERE id_news =-1 OR 1=1

В таком случае будут показаны абсолютно все новости, так как выражение “1=1” всегда истинно.

Разновидности sql-инъекций по атакуемому параметру:

• Внедрение в числовой параметр. (Этот тип sql-инъекции был рассмотрен выше в описании принципа атаки sql-инъекцией)
• Внедрение в строковый параметр.

Например, такой скрипт:

$search_text = $_REQUEST['search_text'];
$res = mysql_query("SELECT id_news, news_id_author FROM news WHERE
                                   news_caption LIKE('%$search_text%')");

            Выполняя такой запрос: https://site.com/index.php?id=')+and+(news_id_author='1, будет выполнен следующий MySql код:

SELECT id_news, news_id_author FROM news WHERE news_caption LIKE('%') and (news_id_author='1%’)

            В таком случае при внедрении sql-инъекции в строковый параметр обязательно должен присутствовать метасимвол «’».

Таким образом, все sql-инъекции можно разделить на данные типы:

• 9 union all select [t]
• 9' union all select [t] and '0'='0
• 9 union all select [t]—
• 9' union all select [t] and '0'='0—
• 9" union all select [t] and "0"="0
• 9) union all select [t] and (0=0

Парсинг ссылок

Так как для внедрения sql-инъекции необходима ссылка с динамическим входным  параметром, а такие проще всего получить с помощью поисковика, чем злоумышленники и пользуются. Мы будем находить ссылки тоже в поисковиках: google, bing, yahoo. Извлекая ссылки с помощью регулярных выражений из html-кодов полученных google, bing, yahoo страниц, будем дополнительно проверять их домен.

Написание программы

При написании нашей программы мы выбирали между двумя языками программирования C# и Python. Мы остановились на C#, из-за необходимости наличия понятного графического интерфейса программы, что с помощью языка Python реализовать достаточно сложно.

Программа может работать в трёх режимах: парсинг, анализ на внедрение sql-инъекции и парсинг+анализ. Сохранение данных ведётся в текстовом формате и XML таблицах.

Так как при  потоке частых запросов в поисковую систему, могут появляться ограничения, вылезать капча, то мы в дальнейшем намерены использовать соединение через прокси-сервера.

Анализ эффективности программы

В интернете нами была найдена программа SQLi Dumper v8.1, только анализирующая ссылки на возможность внедрения sql-инъекции. Сравнивая эффективность, мы получили такие данные: время полного анализа 100 ссылок с 34 заведомо уязвимых при помощью «дампера» ~ 15 минут, наша программа анализировала 9 минут, но при этом первым было найдено все 34 уязвимые ссылки, нашей же программой только 32.

Заключение

Были выполнены выявленные задачи и достигнута поставленная цель. Была написана программа на объектно-ориентированном языке программирования C#, находящая ссылки определённого сайта, анализирующая их на возможность внедрения sql-инъекции. Актуальность программы проверена на практике. Ведётся активная работа над усовершенствованием программы: использованием прокси-серверов.

Создание программы-композитора

Автор: Полтарыхин Матвей Сергеевич

Гимназия ТюмГУ

Научный руководитель: Бородина Елена Николаевна, преподаватель фортепиано МАОУ ДОД ДШИ «Этюд», композитор.

С течением времени музыка терпит изменения за счёт новых технологий. Происходит её модернизация, появляются новые инструменты, способы записи мелодий и их воспроизведения. Отпала необходимость иметь реальные инструменты под рукой. Весь оркестр теперь легко помещается в телефоне или планшете. Неизменным остаётся лишь одно – музыку сочиняет человек. На сегодняшний день не создано ни одного программного продукта, в чьи функции входила бы генерация мелодий. Создание такового могло бы привести к настоящей революции в музыкальной и IT-индустрии, а также это, вероятно, один из путей к созданию искусственного интеллекта, ведь создание музыки на данный момент - процесс, присущий только лишь человеческому мозгу. Поэтому вопрос создания программы-композитора актуален.

Цель этой работы заключается в том, чтобы создать многофункциональную программу, в основе которой будет лежать алгоритм, результатом выполнения которого является последовательность нот, при воспроизведении которых получается музыкальная мелодия, на слух не отличимая от человеческой.

Для достижения этой цели необходимо решение следующих задач:

1.Определить на основе анализа классических произведений особенности, которые присущи большинству гармонических мелодий.

2.Составить алгоритм для получения последовательности нот.

3.Создать на основе алгоритма программу, способную создавать, сохранять и воспроизводить музыку.

В ходе работы было проанализированы несколько классических произведений на предмет закономерностей, схожих особенностей, которые позволили бы выстроить общие критерии для гармоничной, то есть красивой мелодии. Для анализа были использованны знания о музыкальной грамоте и гармонии, общие правила написания музыки.

После сбора теоретических данных была создана программа-композитор, в чьи функции входит генерация мелодии, её прослушивание, визуализация в виде нот, сохранение в память для последующего повторного воспроизведения. При этом был использован движок Unity (2D режим), а все скрипты написаны на языке C#.

Путём опроса было проведено тестирование готовой программы, в ходе которого было выявленно, что более половины опрашиваемых не смогли отличить мелодию, сочинённую программой от мелодии человеческого авторства.

Готовая программа может быть использована как генератор мелодий для обучающегося игре на фортепиано и уже опытного композитора для помощи в написании музыки. Помимо всего, данное исследование приближает нас ещё на один шаг к пониманию и улучшению методов имитирования сложнейших процессов, которые происходят в мозге человека.

Использованная литература:

1. Л.Бетховен, Сонатины для ДМШ, -СПб.: Союз Художников, 2006.
2. А.Моцарт, Сборник фортепианных пьес, -М.: Композитор, 2004.
3. Бритва Н.А., Пособие по теории музыки и сольфеджио, -Тюм.: Сибирский издательский дом, 1997.

Ученица 5 «А» ГБОУ школы №97

Горячева Анна

Руководитель:

Курбатова Екатерина Владимировна

Учитель математики ГБОУ школы №97

Участвуя в олимпиаде «Музеи. Парки. Усадьбы», мы посетили большое количество музеев и обратили внимание на то, что в рассказах о самых интересных памятниках художественного искусства часто встречаются слова «гармония», «пропорции» и даже «геометрия». Оказывается, многие художники считали, что живопись тесно связана с математикой. 

Цель работы: выявить, использовали ли принципы «золотого сечения» русские иконописцы в какой-либо период.

Задачи:

• Провести собственные измерения иконописных изображений для выявления пропорций «золотого сечения»
• Выяснить, что такое «золотое сечение», и какие пропорции в изображении человека должны соответствовать «золотому сечению»;
• Выбрать фотографии икон, созданных в разное время, на которых можно провести измерение пропорций;
• Провести расчеты пропорций изображенных на иконах человеческих образов;
• Проверить принцип.
• Узнать экспертное мнение иконописцев и реставраторов.

Методы:  измерение (сопоставление); анализ; экспертная оценка.

Этапы исследования:

• Поиск и анализ литературы по данному вопросу. В первую очередь это  книга, в которой голландский пастор Герхард Ян Рёттинг разбирает икону А. Рублева "Троица" с позиции "золотого сечения"; исследование Ф. В. Ковалева «Золотое сечение в живописи»; и статья иконописца Александра Бескровного.
• Посещение храмов и музеев (музей древнерусской культуры им. Андрея Рублева, Третьяковская галерея), отбор икон и создание фотографий;
• Проведение исследований на фотографиях икон и формулировка собственных выводов;
• Интервью с иконописцем Никольским Сергеем Владимировичем, который начал выставляться в 1982 году. Недавно в Зале на Гоголевском бульваре прошла его персональная выставка, а также с двумя реставраторами: Никольской Татьяной и Мельниченко Алексеем.

Проведенно исследование на предмет соответствия «золотому сечению»  пропорций фигур на иконах, которое, насколько нам известно, до сих пор еще не проводилось (проводилось исследование композиций). Наша первоначальная гипотеза, что изображения на иконах написаны в соответствии с правилами «золотого сечения», не подтвердилась.

Дальнейшее направление работы: 1) выяснить основные принципы построения композиции живописного произведения в соответствии с принципами золотого сечения и провести собственный анализ композиций многофигурных икон, созданных в разные столетия; 2) закончить исследование икон 18-19 веков.

Данное исследование натолкнуло нас на мысль о проверке общепринятого представления о наличии пропорций «золотого сечения» в практически всех славящихся своей красотой памятниках архитектуры.

Литература

1. Ковалев Ф. В. «Золотое сечение в живописи», электронный ресурс http://hudozhnikam.ru/zolotoe_sechenie.html
2. Золотое сечение. http://www.abc-people.com/data/leonardov/zolot_sech-txt.htm
3. Шкруднев Ф. Д. Золотое сечение http://samlib.ru/s/shkrudnew_f_d/osnovy-30.shtml
4. Золотое сечение:как это работает Московский иконописный портал http://www.mosip.ru/index.php?newsid=547
5. Смирнов А.А. Геометрия и искусство http://class.slovarik.org/dannye-9/data-id10152
6. Герхард Ян Рёттинг «Единение в любви» .
7. Иконостас: золотое сечение, перспектива, иконопись и природные материалы. Тонковид С.Б., Гамов И.Е., Игнатова М.И., Гуляева Е.Ю.
   В сборнике: Развитие креативности личности в современном образовательном пространствесборник материалов международной научной конференции. 2015. С. 66-71.
8. Зорий Файн. Правило Золотого сечения на примере русской живописи и его влияние на современную фотографию http://fine.com.ua/rus/novosti/pravilo_zolotogo_secheniya/
9. Бескровный А., О золотом сечении и пропорциях, или Нужен ли иконе Пифагор? http://pravv.km.ua/read/0014/13-2.html.

   В школьном курсе математики решению логарифмических уравнений и неравенств отводитися важное место. Ученики знакомятся с логарифмами в 11 классе, соответствующие задания встречаются на ЕГЭ. Нужны ли логарифмы сегодня, когда вычислительная техника справляется с самыми сложными расчетами? Так зачем изучают логарифмы сегодня в школе?

Вышесказанное определяет актуальность выбранной темы.  

Объект исследования. Логарифмы и логарифмическая функция.

Предмет исследования. Конкретные задачи, решаемые при помощи логарифмов.        

Цели исследования:   

   Обучающие (изучить теоретический материал по теме, проанализировать данную тему в учебниках по алгебре и началам анализа, рассмотреть применение их свойств. Расширить представление о логарифмах по сравнению со школьной программой);          

   Развивающие (развитие творческого, логического мышления, математической речи);  

   Личностные (воспитание позновательного интереса к предмету);        

   Выяснить, действительно ли логарифмы - универсальный математический инструмент для решения практических задач.      

   Для достижения поставленных целей ставим следующие задачи:    

   Изучить историю возникновения логарифмов.          

   Изучить и освоить методы решения математических задач с логарифмами.    

   Выяснить, в решении каких практических задач могут применяться логарифмы.  

   Если такие задачи существуют, оценить преимущество применения логарифмов на примере конкретных задач.

Гипотеза : Логарифмы - это универсальный математический аппарат, и его можно применять при решении задач из различных сфер деятельности.  

Методы исследования.        

1. Теоретический: анализ литературных источников, анализ и обобщение методов решения, исторический анализ;                

2.  Эмпирический: сравнение методов решения задач.  

Новизна   моей работы заключается в представлении раздела математики, касающегося логарифмов, в более привлекательном виде для изучения старшеклассниками. Компактно и доступно изложен материал по истории логарифмов, теории, применению логарифмов к решению задач из различных сфер науки с целью упрощения решения этих задач.  

Область практического применения.  Подготовленный мною материал могут  использовать старшие школьники при решении задач, в которых применяется математический аппарат (показательная функция и логарифмы), на факультативных занятиях, на занятиях математического кружка и учителя при работе со школьниками при изучении данной темы.                                                   

Алгоритмы поиска клик и их применение в социальных науках

Зубрилина Софья Феликсовна

Россия, Липецкая область, г. Липецк

МАОУ лицей №44, ЦДО “Стратегия”, 9 класс

Научны руководитель Шуйкова И.А., к.т.н., доц.кафедры прикладной математики Липецкого государственного технического университета. 

Графы крайне удобны для представления широкого спектра систем в различных областях. Биологические, социальные, технологические и информационные сети могу быть представлены в качестве графов, поэтому анализ графов стал ключевым механизмом для изучения свойств этих систем. Во многих областях науки теория графов используется для решения прикладных задач. Решение некоторых из них сводится к поиску максимального количества попарно взаимосвязанных объектов (клик) или наоборот множеств объектов, никак не связанных между собой (независимых множеств). Исключительно велико значение быстрых и эффективных алгоритмов, решающих задачу поиска максимальной клики в графе. Известно, что алгоритмы, имеющие хорошую асимптотическую сложность, часто оказываются неэффективными. Целью работы является анализ существующих алгоритмов поиска наибольшей клики в графе, изучение их прикладного назначения и программная реализация указанных алгоритмов. В работе были поставлены и выполнены следующие задачи:

1. Изучить графы и их некоторые основные свойства, рассмотреть прикладные задачи, формализуемые с помощью графов.
2. Изучить числа Рамсея, теорему Рамсея, существующие оценки на числа Рамсея.
3. Изучить существующие алгоритмы поиска максимальной клики в графе.
4. Создать программную реализация одного из изученных алгоритмов, решающую задачу о поиске максимального сообщества в графе социальной сети ВКонтакте.

Проблема поиска максимальной клики в графе имеет множество приложений. Например, в социологии одним их важнейших направлений является анализ социальных сетей, при котором проводится покрытие всего социального графа максимальными кликами. Эта задача сводится к задаче поиска максимальных клик в графе, построенном на основе социальной сети. Основным результатом данного исследования является создание компьютерной программы, которая находить наибольшую клику в графе, построенном на основе социальной сети ВКонтакте. Новизна работы заключается в том, что разработан прототип компьютерного Приложения поиска клик в социальных сетях. Созданная программа позволяет искать большие группы попарно взаимосвязанных людей, при помощи которых, возможно, например, быстро распространять нужную информацию. Это может быть использовано в рекламных компаниях, политике и других вопросах управления социальными группами.

Исследование опирается на следующие библиографические источники:

1. Асанов М., Баранский В., Расин В. — Дискретная математика: Графы, матроиды, алгоритмы — СПб.: Издательство "Лань", 2010.
2. Райгородский А.М. Вероятность и алгебра в комбинаторике. – М.: МЦНМО, 2008.
3. Дасгупта С. И др. Алгоритмы\ С. Дасгупта, Х. Пападимитриу, У. Вазирани; Пер. с англ. под ред. А. Шеня. – М.: МЦНО, 2014. ISBN 978-4439-0236-4
4. Березина Л. Ю. Графы и их применение.: Популярная книга для школьников и преподавателей. Изд. стереотип. - М.: Книжный дом  “ЛИБРОКОМ ”, 2014.
5. Дискретная математика для программистов / Ф. А. Новиков – СПб:  Питер, 2000.

Приложение-шагомер “Solar Steps”, использующее погодные данные для инновационного подсчета калорий

Автор: Стукалов Денис Андреевич.

Образовательное учреждение: ГУО гимназия №10 г. Минск.

Научный руководитель: Стукалов Андрей Александрович, программист-аналитик, начальник отдела информационной безопасности в ООО “Белинвестбанк”.

Цель: разработать инновационное энергоэффективное приложение-шагомер для подсчета калорий с использованием погодных данных метеосервисов.

Задачи: изучить существующие алгоритмы измерения шагов и пройденного расстояния с помощью встроенных датчиков в смартфоне (гироскоп, акселерометр). Изучить сущность формулы Харриса Бенедикта и использовать её для подсчета суммарного количества сожжённых калорий, зависящих от продолжительности сна, количества пройденных шагов, а главное, от температуры окружающей среды.

Суть исследования: кол-во калорий, сожжённых человеком, подразделяется на 3 фактора: кол-во сна, кол-во пройденных шагов, температура окружающей среды. Если первые два фактора каким-то образом задействованы в похожих приложениях, то третий является инновационным и наиболее близко подводящим к наиболее точным результам. 

Актуальность: исследование и разработка приложения являются одними из наиболее актуальных тем в текущем времени, т.к. с течением времени возрастает кол-во людей с ожирением. К примеру, в России процент людей, страдающих избыточной массой тела или ожирением составляет 24,9 %. Поэтому, чтобы бороться с этой достаточно распространённой всемирной проблемой, нужно предпринимать какие-то меры, одной из которых является это приложение.

Значимость и новизна: в настоящий момент аналогов этому приложению нет, т.к. оно использует максимально большое кол-во факторов, влияющих на точность измерения сожжённых калорий, и превносит в жизнь обычных людей немного устремлённости и позитива. Также приложение является достаточно простым для понимания, нересурсоёмким и энергоэффективным, т.к. при длительном отсутствии активности фоновая активность приложения приостанавливается и при возобновлении активности вновь продолжается, поэтому, исходя из экспериментального опыта, приложение максимизировано для простоты усвоения, энергоэффективности и, с точки зрения новизны, действительно первое в своём роде.

Итоги исследования: в результате разработки приложения было использовано большое кол-во различных материалов и формул, способствующих созданию приложения, намного более точно вычисляющего кол-во сожжённых калорий и дающее надежду многим людям, страдающим ожирением, шанс на скорейшее выздоровление. Согласно проведённому опросу, не менее 86% людей действительно заинтересованы в таком приложении.

Ссылка на исходный код приложения: https://github.com/skat1452/SolarSteps

Ссылка на apk приложения: https://drive.google.com/file/d/0Bxd5UMCC_M7kYi15aTFDakpZalE/view?usp=sharing

Использованная литература в результате разработки приложения:

http://startandroid.ru/ru/uroki/vse-uroki-spiskom

http://zdorovko.info/formula-xarrisa-benedikta/

http://gotowalk.blogspot.com.by/2014/06/Opredelenie-kolichestva-szhigaemyh-kalorij-pri-hodbe-bege.html

https://www.quora.com/How-much-energy-does-it-take-to-raise-the-temperature-of-an-average-room-by-10-degrees

http://www.nature.com/ejcn/journal/v56/n4/full/1601308a.html

http://www.wikipedia.com

Скриншоты будут прикреплены здесь же.

1.       Аналоговый левитрон

2.       Сухановский Николай Леонидович

3.       МБОУ “Симферопольская академическая гимназия”

4.       Лавут Елена Сергеевна ГБОУ РК МАН “Крымская юношеская обсерватория”

Цель работы

            Изучить способы магнитной левитации. Создать концепт левитрона и его рабочую модель.

Задачи работы

            Изучить теорию магнитной левитации.

         Создать схему левитрона.

         Реализовать схему в работающую модель

В работе были рассмотрены 3 основных способа магнитной левитации. В итоге в качестве способа для реализации был выбран метод основывающейся на использование активного управления электрическим полем тела.

В результате была построена установка, состоящая из: неодимового магнита, 3-Arduino, 4-полевого транзистора, 1-электромагнитной катушки в 40 Ом, 2-датчика Холла.

Принцип работы левитрона заключается в том, что сначала считывется значения с датчика Холла,  то есть растояние от магнита до полюса катушки, далее в программе на Arduino на основе значений с датчика подаются значения на транзистор и в результате регулируется напряжение на катушке.

Магнит при этом притягивается катушкой, а потом падает обратно под силой тяжести.

Актуальность

Магнитная левитация сейчас используется в транспорте и магнитных подшипниках и также используемая в многих новых концептах и разработках

Преимущество этой установки в том, что магнит левитирует на определенной высоте, которая задана и в дальнейшем возможно ее изменение.

Итоги

В итоге работы были получены следующие результаты:

Была изучена информация о магнитной левитации.

Была разработана схема левитрона.

Был собран рабочий макет левитрона.

Левитрон работает не идеально, так как левитация происходит у полюса катушки.

Математика в биоинформатике: как собирают геном

Павлов Л.Е., Шамаев С.А.

Россия, Липецкая область, г. Липецк

Лицей № 44 города Липецка, ГОБОУ «Центр поддержки одаренных детей», 5 класс

Научный руководитель: к.т.н., доц.кафедры прикладной математики Липецкого государственного технического университета Шуйкова И.А.

Целью работы является изучение графов де Брейна и иллюстрация с их помощью решения задачи биоинформатики «сборка генома».

Методы, используемые в работе: в работе используются методы комбинаторики для анализа исследуемых объектов, начальные знания по теории графов, методы оперирования с простейшими геометрическими фигурами.

В ходе исследования были поставлены и решены следующие задачи работы:

1. изучение литературы и видеоматериалов по теме исследования: – изучение истории развития биоинформатики; – изучение модели представления ДНК как строки для компьютерной обработки; – знакомство с графами де Брейна; ‑ изучение алгоритмов построения строки, включающей в себя заданные подстроки.
2. проведение серии практических работ по исследованию алгоритма построения строки, включающей в себя заданные подстроки.
3. выполнения учебной работы по «сборке генома».

Основной текст тезисов

Исследовательская работа является продолжением практического исследования, начатого авторами в младшей школе. Первый год работы был посвящен проблеме четырех красок. Мы, как и математики, начали с проверки утверждения четырех красок для различных карт, раскрашивая их. Затем, мы изучили жадный алгоритм раскраски вершин графов, при помощи которого теперь мы можем расскрашивать графы. Работа по данной теме была доложена в 2016 года на конференции «Старт в науку» МФТИ. Прикладное значение алгоритмов раскраски графов довольно широко и, в частности, одной из современных и развивающихся в настоящее время областей приложения данного алгоритма является бионформатика. Биоинформатика использует математические методы и компьютерные алгоритмы для решения биологических задач. Задача этого исследования заключалась в использовании графов для моделирования задачи сборки генома. В следующем исследовании мы надеемся изучить применение алгоритма раскраски вершин графа в задачах биоинформатики.

Для описания ДНК в виде нуклеотидной последовательности (последовательности символов) применяют секвенирование. Секвенирование производят при помощи секвенаторов – специальной аппаратуры и технологий. Но геномные секвенаторы в настоящее время еще не могут получить полную последовательность ДНК. Вместо длинных фрагментов получают много коротких фрагментов. Задача биоинформатиков заключается в том, чтобы по данным коротким фрагментам получить одну длинную цепочку ДНК. Мы сделали учебный пример сборки генома, используя двоичный алфавит и тримеры (трехбитовый слова, составленные из 0 и 1) на графах де Брейна при помощи поиска гамильтонова и эйлерова цикла в графе.

Итогом исследования является применение алгоритма поиска эйлерова цикла к графам де брейна для поиска циклическое двоичной последовательности наименьшей длины, составленной из фрагментов – двоичных тримеров.

Исследование опирается на следующие библиографические источники:

1. Артем Касьянов: "Как собрать геном из миллиарда кусочков? Компьютеры и современная биология." [Электронный ресурс]. Режим доступа: https://www.youtube.com/watch?v=kq2D2ucX6qI
2. Александр Омельченко. Граф де Брейна. Курс «Основы теории графов» [Электронный ресурс]. Режим доступа: https://stepik.org
3. Алгоритмы в биоинформатике. [Электронный ресурс]. Режим доступа: Лекция 1. https://www.lektorium.tv/lecture/14229

Данная работа посвящена задаче: для произвольной дроби  $\frac{a}{b}$  определить значение периода и предпериода. Известное решение этой задачи сводит её к решению другой задачи: нахождению минимального показателя $m$ , при котором ${10}^m-1$ делится на $b$ . Последняя же задача ещё далека от своего решения, этим обусловлена актуальность работы. 

Ученик 11 класса: Ахметшин Айдар Альфредович

МБОУ Гимназия №3 ЗМР РТ

Учитель физики: Тезёва Ирина Анатольевна

Цели и задачи исследования 

1. Изучить функцию и строение магнитного поля земли
2. Изучить принцип защиты планеты от космических излучений магнитным полем Земли (Солнечный ветер)
3. Выделить проявления воздействия излучений на полюсах
4. Изучить природу полярного сияния
5. Ответить на вопросы: можно ли сделать искусственное полярное сияние и как это реализовать?
6. Выявить перспективы создания искусственного полярного сияния

Магнитное поле Земли

Большинство планет Солнечной системы в той или иной степени обладают магнитными полями. По убыванию дипольного магнитного момента на первом месте Юпитер и Сатурн, а за ними следуют Земля, Меркурий и Марс. Под действием исходящего от Солнца потока плазмы (солнечного ветра) магнитное поле Земли искажается и приобретает «шлейф» в направлении от Солнца, который простирается на сотни тысяч километров, выходя за орбиту Луны. Специальный раздел геофизики, изучающий происхождение и природу магнитного поля Земли называется геомагнетизмом. Геомагнетизм рассматривает проблемы возникновения и эволюции основной, постоянной составляющей геомагнитного поля.

Происхождение магнитного поля Земли

Динамо-эффект – самовозбуждение и поддержание в стационарном состоянии магнитных полей вследствие движения проводящей жидкости или газовой плазмы. Его механизм подобен генерации электрического тока и магнитного поля в динамо-машине с самовозбуждением. С динамо-эффектом связывают происхождение собственных магнитных полей Солнца Земли и планет, а также их локальные поля, например, поля пятен и активных областей.

Солнечный ветер

Солнечный ветер - истечение плазмы солнечной короны в межпланетное пространство. На уровне орбиты Земли средняя скорость частиц солнечного ветра (протонов и электронов) около 400 км/с, число частиц – несколько десятков в 1 см³. Честно говоря наше светило очень щедрое, ведь помимо излучения (солнечного излучения) оно испускает в пространство огромное количество себя. Каждую секунду она теряет около одного миллиарда килограмм протонов и нейтронов. Это называется солнечным ветром. Но ничего приятного в этом нет, ведь по сути это разряженная плазма, которая летит с огромной скоростью во всех направлениях.

Полярное сияние

Полярное сияние - свечение верхних разреженных слоев атмосферы, вызванное взаимодействием атомов и молекул на высотах 90-1000 км с заряженными частицами больших энергий (электронами и протонами), вторгающимися в земную атмосферу из космоса. Соударения частиц с составляющими верхней атмосферы (кислородом и азотом) приводят к возбуждению последних, т.е. к переходу в состояние с более высокой энергией.

Искусственное полярное сияние

Наиболее убедительным доводом в пользу того, что мы понимаем какое-нибудь физическое явление, является его повторение в лаборатории. Это удалось сделать и для полярного сияния - создать его искусственно в лаборатории с масштабами нашей планеты. Этот эксперимент, получивший название "Аракс", начат в 1985 году совместно российскими и французскими исследователями.

Значимость и новизна исследования

Полярные сияния сигнализируют о месте и времени воздействия Космоса на земные процессы. Вызывающее их вторжение заряженных частиц влияет на многие стороны нашей жизни. Изменяется содержание озона и электрический потенциал ионосферы, нагрев ионосферной плазмы возбуждает волны в атмосфере. Все это сказывается на погоде. Из-за дополнительной ионизации в ионосфере начинают течь значительные электрические токи, магнитные поля которых искажают магнитное поле Земли, что прямо влияет на здоровье многих людей. Таким образом, через полярные сияния и связанные с ними процессы Космос воздействует на окружающую нас природу и ее обитателей.

Итоги исследования 

Для создания уникального небесного явления нужно запустить на орбиту Земли ускоритель элементарных частиц. Кроме того, техника позволит рисовать на небе не просто различные разводы, но и интересные рисунки. Данное направление будет очень востребовано в современном обществе, так как технический прогресс и развитие науки преподносят нам новые открытия в разных сферах общества. Ежедневно мы сталкиваемся с чем - то новым, но изучение магнитного поля Земли и разработка нового и улучшение старого способа получения искусственного полярного сияния в любой точке мира, даст возможность всем людям полюбоваться и восхититься, наверное, одним из самых незабываемых световых шоу на земле, помимо этого искусственные полярные сияние смогут и разнообразить наши праздники и удивлять гостей нашей страны на различных соревнованиях.

Список литературы

Соросовский образовательный журнал, Том 7, N 5, 2001 г. 

Онлайн энциклопедия: http://www.krugosvet.ru/

Научная сеть: http://nature.web.ru/

Новостной интернет-журнал о науке: qwrt.ru

Исследовательская работа

АЛГОРИТМ ОПРЕДЕЛЕНИЯ И ПРОГНОЗИРОВАНИЯ ВАЛЕНТНОСТИ ЭМОЦИИ НА ОСНОВЕ ДАННЫХ ЭЛЕКТРОЭНЦЕФАЛОГРАММЫ

и реализованный на основании проведенного исследования проект

программное обеспечение, реализующее канал биологической обратной связи на основе нейроинтерфейса

Автор проекта: Пасечнюк Дмитрий Аркадьевич

Учреждение: МБОУ СОШ «Школа будущего», 8 класс, п. Большое Исаково, Калининградская обл.  

Научный руководитель: Ботман Степан Александрович, инженер лаборатории нейробиологии и медицинской физики БФУ им. И.Канта, г. Калининград

Актуальность

           Современные достижения в области регистрации потенциалов головного мозга и развитие вычислительных средств и методов, открывают новые возможности для создания принципиально новых систем управления информационной средой на основе мозг-компьютерных интерфейсов. Основной проблемой построения таких систем является получение объективной оценки нейрофизиологических коррелятов эмоционального восприятия визуальных сигналов.

          Разработки, подобные представленной, найдут свое применение в областях нейромаркетинга, и окажут существенное влияние на сферы деятельности, требующие объективной оценки компетенций человека ввиду исключения человеческого фактора, таких как экзамен, собеседование, защита проекта.

Цель

         Цель исследовательской работы - поиск оптимального из наиболее распространенных при анализе временных рядов алгоритмов анализа данных при определении и прогнозировании валентности эмоционального отклика на графический стимул на основе данных ЭЭГ-сигнала человека.

         Цель проектной работы - создание программного продукта, реализующего канал биологической обратной связи на основе нейроинтерфейса, позволяющего определить эмоциональный отклик на визуальный стимул на основе данных сигнала ЭЭГ и отобразить полученную информацию на компьютере пользователя.

Задачи

1.Изучение существующих подходов и современных инструментов анализа ЭЭГ человека;

2.Определение наиболее значимых признаков ЭЭГ-сигнала при классификации эмоционального отклика на графический стимул;

3.Сбор и первичный анализ (разметка) экспериментальных данных, включающих в себя значения выделенных признаков ЭЭГ и валентность (тон) эмоционального отклика, испытываемого в определенный момент времени;

4.Выбор оптимального алгоритма анализа данных;

5.Разработка пользовательского интерфейса программы.

Методы

            В качестве аппаратной части используется уникальное оборудование - устройство для регистрации биопотенциалов Balalaika v1.0 (разработка БФУ им. И. Канта).

           Для определения оптимального алгоритма машинного обучения производилась запись обучающих выборок, включающих в себя протоколы биопотенциалов человека и валентностей испытываемых им эмоций.  Далее, для обучения алгоритма выделялись признаки ЭЭГ-сигналов и им сопоставлялись валентности эмоциональных откликов.

           Для реализации программной части нейроинтерфейса написана программа на языке Python 3 с использованием библиотеки scikit-learn, работающая следующим образом:

1. Получение и буферизация данных с устройства;
2. Сегментация данных методом скользящего окна;
3. Расчет признаков сигнала ЭЭГ (ассиметрия по полушариям, авторегрессионные коэффициенты седьмого порядка и др.);
4. Классификация данных с использованием многослойного персептрона;
5. Вывод на экран предсказанного эмоционального отклика.

Результаты

           В результате выполненной работы определены наиболее значимые признаки сигнала ЭЭГ. В качестве алгоритма классификации выбран многослойный персептрон, в силу оптимальности показателей чувствительности и точности.

           С учетом полученных результатов разработана и реализована программа, написанная на языке программирования Python 3 с использованием библиотеки анализа данных sklearn, обладающая простым интерфейсом, определяющая валентность (тон) эмоции человека и отображающая полученную информацию на экране монитора в реальном времени исключая физическое взаимодействие пользователя со стандартными интерфейсами ввода.

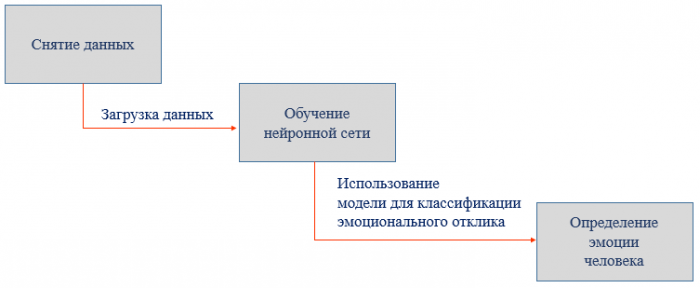
ЗАДАЧА ТОМСОНА 

Масленникова Елизавета Алексеевна 

МБОУ "Физико-математический лицей"

научный руководитель: Забавин Валерий Николаевич

Цель работы: доказать равновесность известных расположений на сфере трех, четырех и шести одинаковых зарядов и предполагаемого расположения пяти зарядов.

В начале XX века, конструируя модель атома, английский физик Джозеф Джон Томсон рассматривал задачу о равновесном расположении зарядов на сфере, то есть о таком расположении, когда потенциальная энергия зарядов наименьшая. . В некоторых случаях равновесное расположение известно (для небольшого числа зарядов). В части этих случаев равновесность доказана. В работе [1] сообщается, что для трех и четырех зарядов доказательства выполнены с помощью неравенств между средним арифметическим, средним геометрическим и средним гармоническим, но самих доказательств не приводится. В этой же работе выполнены доказательства для шести и двенадцати зарядов с помощью методов, известных узкому кругу специалистов.

Точное решение задачи Томсона для пяти зарядов в известной автору литературе отсутствует. Считается, что заряды расположены так: два заряда в концах диаметра сферы,  три - в плоскости, проходящей через центр сферы перпендикулярно этому диаметру, в вершинах правильного треугольника.

При рассмотрении трёх, четырёх и шести зарядов используются методы элементарной математики; рассмотрение пяти зарядов потребовало привлечения методов математического анализа.

Вывод:  доказана равновесность известных расположений на сфере одинаковых зарядов для трёх зарядов (вершины правильного треугольника, плоскость которого проходит через центр сферы), четырёх зарядов (вершины правильного тетраэдра), шести зарядов (вершины правильного октаэдра) и предполагаемого расположения пяти зарядов. Для шести зарядов доказана единственность расположения зарядов (для трех, четырех и пяти зарядов она не требует доказательств).

Литература

1.​ Н. Н. Андреев, В. А. Юдин. Экстремальные расположения точек на сфере // Математическое просвещение (третья серия). Вып. 1 – М.: МЦНМО, 1997.

Геометрическое решение задач с параметрами

Автор работы: Оськина Арина Николаевна, 10 класс МОУ «Лицей №7» г. Саранск

Руководитель: Леонова Татьяна Ивановна, учитель математики МОУ «Лицей №7»

Цель работы: рассмотреть различные геометрические методы решения алгебраических задач с параметрами.

Задачи исследования:

• изучить научную литературу, в поисках таких методов, которые позволили бы оптимизировать решение задач с параметрами;
• научиться решать задачи с параметрами графическим (придание геометрического смысла) методом;
• отработать приемы геометрического метода решения алгебраических задач;
• показать, что преимущество геометрического метода в его наглядности.

Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры, но их решение вызывает значительные затруднения. Это связано с тем, что каждая задача  с параметрами представляет собой целый класс обычных задач, для каждой из которых должно быть получено решение.

В данной работе рассматривается решение некоторых алгебраических задач с параметрами методами, основанными на наглядной геометрической интерпретации. Рассмотрены различные подходы к решениям, проведена классификация задач с параметрами, решаемые геометрическим способом.

Актуальность: умение решать задачи с параметрами во многом является залогом достижения высокого результата на ЕГЭ, на математической олимпиаде.

Новизна  работы заключается в углубленном изучении математики на основе интеграции алгебраического и геометрического методов решения задач.

Итоги: можно выделить несколько преимуществ в решении задач с параметром геометрическим способом:

• наглядность графического способа решения позволяет определить изменения аргумента в зависимости от параметра;
• график дает возможность аналитически сформулировать необходимые и достаточные условия для решения поставленной задачи;
• на основании графической информации можно сделать выводы о количестве решений, их границах и т.д.

Нами была составлена классификация алгебраических задач с параметром по способу их решения.

Список использованных источников

1. Горелов М. О пользе графиков.// Квант. №3. – 2010. – С. 44-47.
2. Прокофьев А.А. Задачи с параметрами. Подготовка к ГИА и ЕГЭ/ А.А. Прокофьев – БИНОМ. – 2014. – 400 с.
3. Сергеев И. Н. Математика. Задачи с ответами и решениями: учебное пособие. – М.: КДУ; Владимир: ВКТ, 2008. – 368 с.
4. Фельдман И.В. ЕГЭ? ОК! [Электронный ресурс]/ И.В. Фельдман//Режим доступа: URL: https://ege-ok.ru/category/zadachi-s-parametrom/page/2

Гемодинамика в сосудах головного мозга

Юськов Александр

МБОУ «Экономический лицей»

Научный руководитель: Дедок Василий Александрович

ИМ СО РАН им. Соболева

В нашей жизни иногда встречаются такие нарушения в развитии сосудов, как мальформации, которые представляют собой плотный клубок расширенных сосудов, в котором вены контактируют с артериями без участия капиллярной сети ввиду ее отсутствия. В результате отклонения, артериальная кровь шунтируется в систему глубоких и поверхностных вен без отдачи питательных веществ и выведения углекислого газа.

В последнее десятилетие в эндоваскулярном лечении пациентов с церебральными артериовенозными мальформациями достигнуты значительные успехи.

В то же время остается достаточно высоким процент осложнений, приводящих к инвалидизации (3,8–7,1%) и смерти (1,5–3,0%). Наиболее тяжкие осложнения связаны с перипроцедуральными кровоизлияниями, частота которых, по разным данным, варьирует от 2,0 до 16,7%

Одной из причин таких кровоизлияний являются изменения гемодинамики, которые происходят в сосудах мальформации и окружающих узел «здоровых» сосудах мозга в результате частичной или полной эмболизации АВМ. Поэтому перед операцией выгодно проводить ее моделирование, для того, чтобы понять, как она скажется на пациенте и какие возможны последствия.

Поскольку существующие модели достаточно сложные то было решено разработать свою, более простую модель. В результате была создана гидродинамическая модель движения крови на заданном участке. В расчетах модели применяется клеточный автомат.

В данном случае сосуды представляют собой последовательность клеток. Состоянием клетки является давление в ней. Кровь с некоторой скоростью перетекает из области с большим давлением в область с меньшим давлением с учетом формулы Пуазейля:$Q=\frac{{\mathrm{\pi r}}^4}{8\eta L}∆P$,где Q – объемная скорость движения жидкости, Р – давление в сосудистой системе, L — длина сосуда, r — радиус сосуда,η — вязкость крови. Некоторые клетки являются входными: в них генерируется давление, некоторые – выходными: в них давление уменьшается. Учитывается пульсирующий характер движения крови. При резком увеличении давления возможен разрыв сосудов.

В данной программе возможно создание карты сосудов с последующей проверкой стабильности. Интерфейс позволяет визуализировать процессы перемещения крови по сосудам до и после изменений. Также есть возможность посмотреть статистические характеристики данного участка сосудов.

По распределению давления и количеству протекающей через данный участок крови мы можем судить о эффективности операции и возможных последствиях. Обладая этой информацией можно более правильно спланировать будущее вмешательство.

В итоге была создана программа для моделирования сети кровеносных сосудов. С ее помощью возможно моделирование движение крови по сосудам и предсказание результатов эмболизационного вмешательства. На данном этапе программа находится на стадии калибровки.

Литература

• А. Л. Кривошапкин, В. А. Панарин, К. Ю. Орлов, В. В. Берестов, Т. С. Шаяхметов, А. В. Горбатых, Д. С. Кислицин, А. П. Чупахин, А. А. Черевко, А. К. Хе, Г. С. Сергеев, Д. В. Чебыкин – 2013. Алгоритм предупреждения гемодинамических кровоизлияний при эмболизации церебральных артериовенозных мальформаций.
• В.А. Панарин, К.Ю. Орлов, А.Л. Кривошапкин, А.П. Чупахин,А.А. Черевко, А.К. Хе, Н.Ю. Телегина, В.И. Баранов – 2012. Использование гидродинамических расчетов в выборе сценария эмболизации церебральной артериовенозной мальформации c фистульным компонентом
• Харьковский национальный медицинский университет – 2016. Физиология сосудистой системы. Основные принципы гемодинамики.
• В.Б.Кошелев, С.И.Мухин, Н.В.Соснин, А.П.Фаворский – 2010. Математические модели квази-одномерной гемодинамики.

Особенности программной реализации криптографических алгоритмов на языке PascalABC.NET

Автор: Румянцев Данила Анатольевич ученик 10 класса ОГАОУ «Белгородский инженерный юношеский лицей-интернат»
Руководители: учитель информатики и ИКТ высшей квалификационной категории

ОГАОУ «Белгородский инженерный юношеский лицей-интернат»

Тополева Наталья Ивановна

учитель математики  высшей квалификационной категории, Почетный работник общего образования РФ

ОГАОУ «Белгородский инженерный юношеский лицей-интернат»

Елисеева Наталья Петровна

Наименование секции: Секция прикладной математики и информатики

Актуальность и новизна темы обуславливается тем, что на сегодняшний день возможности криптографии сложно переоценить, т.к. она способна обеспечить информационную безопасность компьютерных данных. Практическое применение криптографии стало неотъемлемой частью жизни современного общества — её используют в таких отраслях как электронная коммерция, электронный документооборот (включая цифровые подписи), телекоммуникации и других. Исходя из вышесказанного, криптография является перспективным, важным и востребованным направлением. Данная работа может принести пользу школьникам на этапе подготовки к олимпиадам, приоткроет завесу тайны таких специальностей как криптограф, криптоаналитик, шифровальшик и др.

Цель: изучить и реализовать программно некоторые криптографические алгоритмы с помощью языка PascalABC.NET.

Задачи исследования:

Изучить литературу по теме исследования.

Проанализировать современные методы использования криптографических алгоритмов.

Исследовать несколько популярных способов шифрования, дешифровки и стойкость шифра.

Написать на языке PascalABC.NET программу для шифрования и дешифровки некоторых криптографических алгоритмов.

Разработать и реализовать программно  собственный шифр.

Краткое описание работы. За время работы мы:

• познакомились с историей развития криптографии;
• проанализировали современными способы ее использования;
• исследовали варианты шифрования, дешифровки;
• изучили шифрование методом «Цезаря» и «Атбаш»;
• реализовали программно вышеназванные алгоритмы с помощью языка PascalABC.NET;
• разработали, описали и программно реализовали собственный криптографический алгоритм «Миллениум».

Выводы

Реализация алгоритмов на языке программирования показала, что учет всех событий шифровки и дешифровки алгоритмов находится за пределами школьного курса программирования. В наших силах оказалось возможным реализовать лишь частные случаи шифрования и дешифровки с использованием изученных методов.

Во время работы над созданием собственного шифра несколько попыток придумать свой шифр оказались неудачными, т.к., при детальном анализе, в той или иной степени, они являлись разновидностями уже известных шифров. Разработанный нами шифр имеет общность с шифром Лестера Хилла в том, что букве ставится в соответствие цифра. В остальном схожих черт нет.

Список литературы

1. http://kriptografea.narod.ru
2. http://ru.wikipedia.org

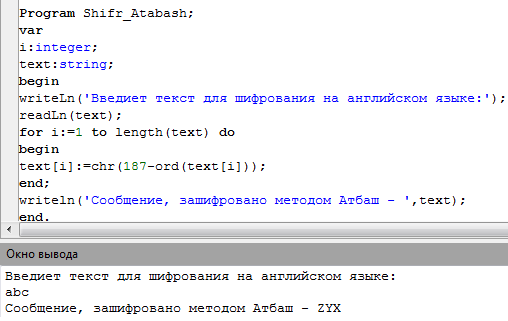
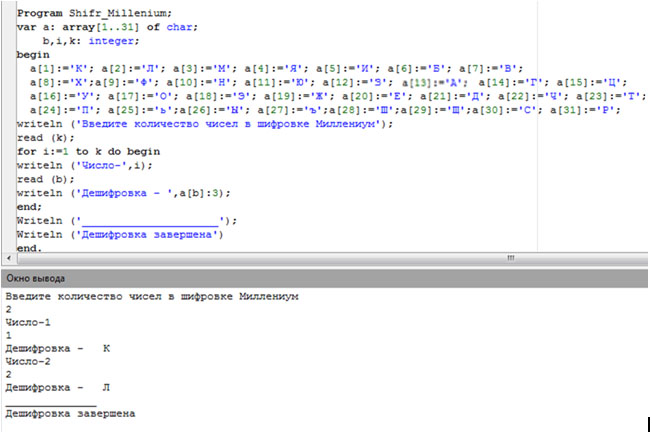
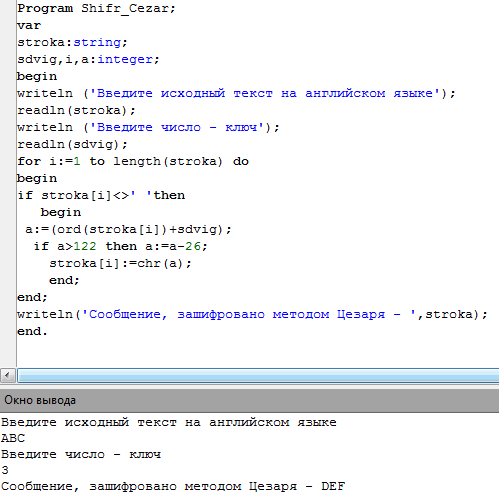
Работа отвечает на вопрос: Почему шифрование с открытым ключем лучше, чем с закрытым?

Как работает метод шифрования  с открытым ключом?

Библиотека для управления мобильными роботами, на примере простейшего робота Linefollower

Автор: Белоусов Евгений Александрович

Гимназия 1576 ФМО, КСР МФТИ

Научный руководитель: Петренко Эдуард Оттович

Цель проекта

• Создание библиотеки для управления мобильным роботом на платформе Arduino. Проверять концепцию программы мы будем на роботе Linefollower.
• Перевести робота linefollower`a «Angel — 1» на новое ПО (программное обеспечение), созданное в результате исследования.
• Создать ПО для нового робота «Light».

Актуальность проекта

Спортивная робототехника — быстроразвивающееся направление научно-технического молодежного творчества. Все больше и больше людей принимают участие в проектировании новых роботов и написании программ под них. Средний код для робота на платформе Arduino занимает 100 — 200 строк. А код для робота, который способен побеждать в соревнованиях может занимать до 2000 строк. Вероятность допущения ошибки в такой программе очень высока, а ее поиск крайне затруднителен. Не говоря уже о том, что это является недопустимым с точки зрения современного программирования. Написание  библиотеки сильно упростит процесс написания и отладки программы, а код сократится до 20 строк.

Требования к простейшему Linefollower

Система должна обеспечивать автономное максимально быстрое следование по контрастной линии.

Анализ

Мобильный робот состоит из сенсоров, микроконтроллера и актуаторов — частей конвейера, слаженная работа которых обеспечивает правильное функционирование системы.

Для дальнейшей работы имеет смысл  выделить три основных вида классов нашей программы: Sensor, Algorithm и Actuator, которые являются частями конвейера.

Дальше мы можем выделить следующие основные классы для linefollower`а: AnalogSensor, ExcAlgorithm, SpeedAlgorithm, Motors. Пронаблюдать иерархии объектов робота мы можем пронаблюдать на рисунке 1.

Проектирование

Для обеспечение гибкости программы был выбран вариант создания объектов данных, с которыми будут взаимодействовать основные классы нашей программы.

Иерархию классов объектов данных можно пронаблюдать на рисунке 2.

Архитектура,построенная нами, представлена на рисунке 3.

Пример работающей программы можно пронаблюдать на рисунке 4.

Готовый код выставлен на github.

Результаты проекта

Создана легко-расширяемая библиотека для управления мобильным роботом, использование которой

• существенно упростит процесс написания программы
• уменьшит время, затрачиваемое на написание кода
• повысит надежность программы

Существенно улучшена программа на роботе «Angel-1»

Создано ПО для нового робота «Light»

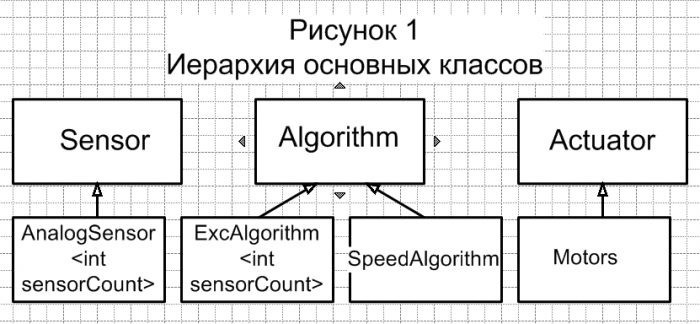
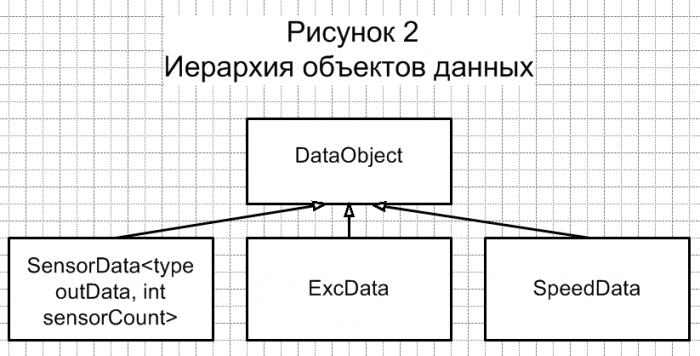
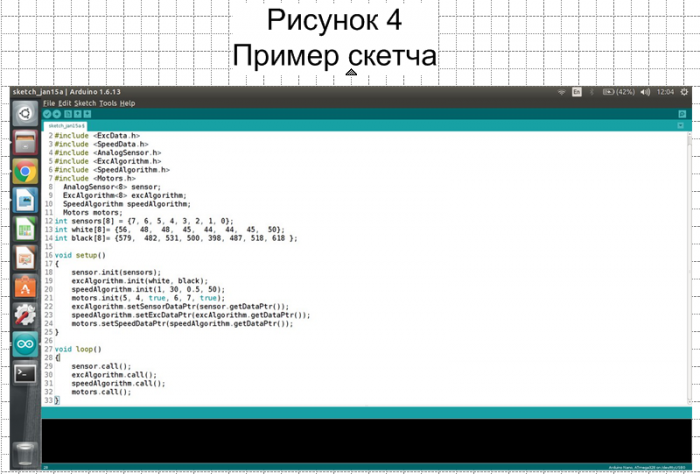
Моделирование белков

Неверов Андрей Вячеславович, 11 класс

МБОУ «Экономический лицей»

Научный руководитель: Дедок Василий Александрович, кандидат ф.-м. наук, институт математики им. С. Л. Соболева СО РАН

Нас заинтересовал вопрос моделирования самосборки белка и возможность ее оптимизации. На данный момент эта задача имеет большое значение, так как процесс фолдинга белков еще полностью не понят, в то время, когда исходя из него можно предсказывать свойства белков, что, следовательно, может помочь в лечении множества болезней.

Молекулярное моделирование начинается с формирования компьютерной модели молекулы путем задания пространственного расположения ее атомов в виде их декартовых координат. Данные о них были взяты из открытых библиотек.

Далее рассчитывается и полная энергия по отношению к атомарным координатам, где:

${}_{}$ E_{total} = E_{str} + E_{bend} + E_{tors} + E_{vdw} + E_{elec}$ ,{}_{}$

где  $E_{total}$- полная энергия молекулы;

$E_{str}$ - энергия связи растягивания;

$E_{bend}$ - энергия угла изгиба;

$E_{tors}$ - энергия кручения;

$E_{vdw}$ - энергия Ван-дер-Ваальса;

и $E_{elec}$ - энергия электростатического взаимодействия.

Основной идей молекулярной механики является то, что связи имеют "нормальные" длины и углы. Таким образом, полная энергия является мерой внутримолекулярного штамма по отношению к гипотетической молекуле с идеальной геометрией. Сама по себе полная энергия не имеет физического смысла.

Дальнейшее моделирование сводится к поиску состояний системы с минимумом энергии. Для этого планируется использовать методы:

Поиска методом Монте-Карло;

Поиска эволюционными алгоритмами;

Моделированием отжига;

После чего выбирается наиболее эффективный.

В любом случае генерация структур со случайными параметрами; позволяет добиться максимального разнообразия конформеров, однако появляется проблема комбинационного взрыва.

В силу сложности моделирования (в зависимости от вычислительных мощностей процесс занимает от нескольких суток до месяцев), создаются модели пептидов, т.е. коротких белков, состоящих из 2-4 аминокислот.

На данный момент реализовано прямое моделирование аминокислоты глицина, состоящего из 10 атомов.

Список используемой литературы

1. Molecular modeling H. D. Holtje and Gerd Folkers 3d edition 1996
2. Моделирование биологических систем на GPU Жмуров А.А., Барсегов В.А. Учебное пособие 2013
3. Лекции по математическим моделям в биологии Г.Ю. Ризниченко 2010

Диагностика заболеваний нейронными сетями

Кандалова Екатерина Алексеевна 10В,

МБОУ «Экономический лицей» г.Новосибирск

Научный руководитель: Дедок Василий Александрович кандидат ф.-м. наук 

Введение

Одним из направлений исследований в области искусственного интеллекта, основанным на попытках воспроизвести нервную систему человека, является нейронная сеть. А именно: способность нервной системы обучаться и исправлять ошибки, что должно позволить смоделировать, работу человеческого мозга.

Значимость и новизна

Наука, а в частности медицина и современные технологии, интенсивно развиваются. За этим развитием следует будущее, именно поэтому подрастающее поколение способствует интенсивному прорыву в этой области.

В настоящее время медицинская диагностика обычно проводится в 
медицинских учреждениях при помощи сложных приборов. Однако, современные  технологии, такие как: умные часы, фитнес-браслеты, телефоны с датчиками  позволяют получать достаточно много информации о сердечном ритме.  Последние научные исследования говорят о том, что используя эти данные, можно много сказать о здоровье человека.
Существуют исследования специалистов по машинному обучению, которые показывают, что ЭКГ-сигнал несет в себе информацию о функционировании всех систем организма, а не только сердца. При этом каждое заболевание по-своему «модулирует» ЭКГ-сигнал, а значит знаки приращений интервалов и амплитуд последовательных кардиоциклов можно использовать для диагностики информации о возможных проблемах со здоровьем у человека, в том числе на ранних этапах их возникновения.

Постановка задачи

В наше время проблема курения стала очень актуальна. Поэтому я решила совместить современные технологии с  современными проблемами. Задача моей работы состоит в том, чтобы создать алгоритм, который мог бы обнаружить курильщика среди некурящих людей на основе их кардиограмм. Обучающая выборка кардиограмм включает: 100 записей, из них 50 курящих и 50 некурящих.

Существуют решения для мониторинга сердечного ритма, например, решение от компании Кардиокварк. Они дают возможность регулярно отслеживать  сердечный ритм пациента даже без визита к врачу. Однако, их решение  требует дополнительного специализированного оборудования, в нашем случае  планируется использовать уже имеющиеся устройства пациента или же любого  из имеющегося на рынке (не обязательно одной модели).

Актуальность проекта
Для постановки диагноза необходимо построить модель 
диагностики. Сильной стороной метода является то, что модель 
формируется путем самообучения нейронных сетей алгоритмами без учителя,  тем самым возможно выделять не только те диагнозы, которые были  определены изначально, но и новые аномалии пациентов, не предъявляемые  ранее модели.

Методика решения                                        

Решение поставленной задачи основывалось на гипотезе о зависимости вариабельности ритма сердца (ВСР) от функционального состояния организма. Данная модель включает в себя обратную связь посредством периферической нервной системы через головной мозг, позволяющую управлять потоком крови, в том числе путем динамического управления частотой ритма сердца. 

Список данных, которые я использовала для построения карты:

1) EnLog — Энтропия «логарифмической энергии»;
2) EnTrs — Пороговая энтропия;
3,4) EnSamp — Две энтропии отсчетов с параметром 1 и 5;
5) NN22 — Число последовательных RR-интервалов, различающихся больше чем на 22 мс;
6) HRVTi — Триангулярный индекс гистограммы ритма сердца;
7) LF/HF — Отношение мощности низкочастотной к высокочастотной части спектра;
8) LFn — Отношение мощности низкочастотной части спектра к сумме мощностей низкочастотной и высокочастотной частей спектра;
9) SBxn — Отношение мощности спектра в диапазоне от 0.093 Гц по 0.125 Гц; 
10) SB1n — Мощность спектра в диапазоне от 0.0039 Гц по 0.0391 Гц.

Проблема в извлечении информации о влиянии никотина и других веществ на организм человека сводится к поиску параметров ВСР, обладающих наибольшей разделяющей способностью классов курящих и не курящих людей. Для создания алгоритма мы использовали самоорганизующиеся карты Кохонена.

Исследование заключалось в вычислении всего набора параметров для классов курящих и не курящих в записях обучающей базы и последующем совместном анализе их распределений. Выбирались только те параметры, плотности распределения которых имели значимые расхождения в какой-либо области.

Рассмотрим как карты Кохонена находят закономерности в исходных данных. Каждый объект характеризуется набором различных параметров, которые описывают его состояние. Таким образом нам надо на основании анализа параметров объектов выделить схожие объекты и представить результат в форме, удобной для восприятия. Будем считать, что объект имеет три признака (на самом деле их может быть любое количество).Теперь представим, что все эти три параметра объектов  представляют собой их координаты в трехмерном пространстве (в том самом пространстве, которое окружает нас в повседневной жизни). Тогда каждый объект можно представить в виде точки в этом пространстве.

После этого этот узел подтягивается к объекту. Затем выбирается другой объект (точка), и процедура повторяется. В результате мы получим карту, расположение узлов которой совпадает с расположением основных скоплений объектов в исходном пространстве.Теперь определяем, какие объекты у нас попали в какие узлы карты. Это также определяется ближайшим узлом – объект попадает в тот узел, который находится ближе к нему. В результате всех этих операций объекты со схожими параметрами попадут в один узел или в соседние узлы. С помощью полученной карты мы можем проанализировать курит человек или нет.

Результат

Из результатов тестирования видно, что в среднем показатели эффективности классификатора находятся в районе 60-70%.
Результат работ демонстрирует наличие теоретической и экспериментально подтвержденной связи между вариабельностью ритма сердца и функциональными изменениями организма, связанными с табакокурением.

Перспективы

Возможности применения алгоритма к другим заболеваниям и методам диагностики.

Персистентная длина полимера

Выполнила: Ю. С. Кащенко, ученица МБОУ “Экономический лицей”

Научный руководитель: кандидат ф.-м. наук Дедок Василий Александрович

Меня заинтересовала возможность получения значения персистентной длины полимера теоретически - при помощи математической формулы. Я решила проверить, возможно ли вывести эту формулу, если смоделировать поведение молекул при помощи метода Монте-Карло.

Высокомолекулярными соединениями, или полимерами, принято называть вещества с молекулярной массой порядка 104 и выше. Эти соединения построены из элементарных звеньев, состав и строение которых зависят от исходных мономеров, количество которых варьируется от 1000 до 1500. [3]

Одной из характеристик, которая помогает знать конфигурацию молекулы, а следовательно, и её химические свойства – персистентная длина полимера. [4]

Персистентной длиной цепочки полимера принято считать среднеквадратичное расстояние между концами этой цепочки.  Величина квадрата среднего расстояния между концами цепи, равна . Это же выражение легко также получить, если длину и направление каждой связи в цепи описать векторами L_i, так что вектор, направленный из одного конца цепи к другому можно представить в виде суммы слагающих цепь векторов.(Приложение. Рисунок 1) Однако, при выведении данной формулы допускаются самопересечения векторов, что на самом деле невозможно в цепи полимера. [5]

Тогда, я решила пересмотреть вид данной формулы, используя случайные блуждания. Для начала, я рассмотрела возможность самонепересекаемых случайных блужданий, они моделируются по методу Монте-Карло [1], который положен в основу моей программы, которая “запускает” случайные блуждания, в трёхмерном пространстве. Для каждого значения n(количества звеньев) строится 1млн значений, из которых затем находится среднеквадратичное расстояние между концами цепи полимера (далее h).

По полученным данным, для количества звеньев от 2х до 50ти с длиной звена единица для каждого, я построила график (Приложение. Рисунок 2). При этом очевидно, что для входных данных 1 и 0, выходные также будут 1 и 0 соответственно. Однако полученный мною график отличается от графика вида (Приложение. Рисунок 3), из чего можно сделать вывод, что общепринятая формула не достаточно точная. А значит, требуется вывести новую, чем я занималась в своей работе.

Подводя итоги - я применила случайные блуждания в области химии, уточнив формулу, описывающую зависимость персистентной длины молекулы от ее количества звеньев, учитывая условие самонепересекаемости звеньев. И хотя, полученая мною формула не сильно отличается от сейчас используемой,  это позволит значительно уменьшить погрешности при расчете упругости полимера, а значит, более точно определять химические свойства молекулы.

Кроме того, в перспективы исследования входит оптимизация программы, а точнее – сокращение время работы, которое сейчас достаточно велико. На данный момент, я рассматриваю возможность распараллеливания построений блужданий (построение блужданий одновременно).

Литература

1. “Компьютерное моделирование в физике. Том 2.” Гулд Х. Тобочник Я. Издательство “Мир”, 1990 год.
2. “Мыльные пленки и случайные блуждания”. А.Б. Сосницкий. Издательство Московского центра непрерывного математического образования, 2000 год.
3. Адельсон С. В., Вишнякова Т. П., Паушкин Я. М. “Технология нефтехимического синтеза: Учеб. для вузов.” — 2-е изд., перераб.—М.: Химия, 1985. —- 608 с., илл.
4. Ахмадеев Р, Г.‚ Данюшенский В.С..”Химия промывочных и тамионажных жидкостей” Учебник для вузов, — М.: Недра, 1981. 152 с.
5. “Руководство по аналитической химии”-Перевод с немецкого: канд. хим. наук В. В. Кузнецова, канд. хим. наук Л. Б. Кузнецовой. Под редакцией заслуж. деятеля науки и техники РСФСР, проф. Ю. А. Клячко. Издательство «Мир» Москва 1975 год.

Приложение:

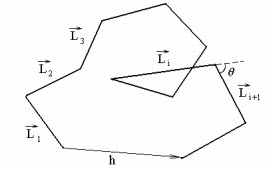  рисунок 1 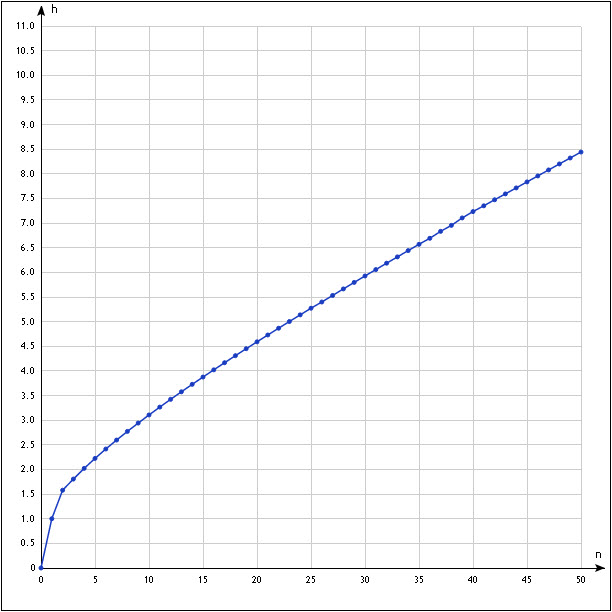рисунок 2

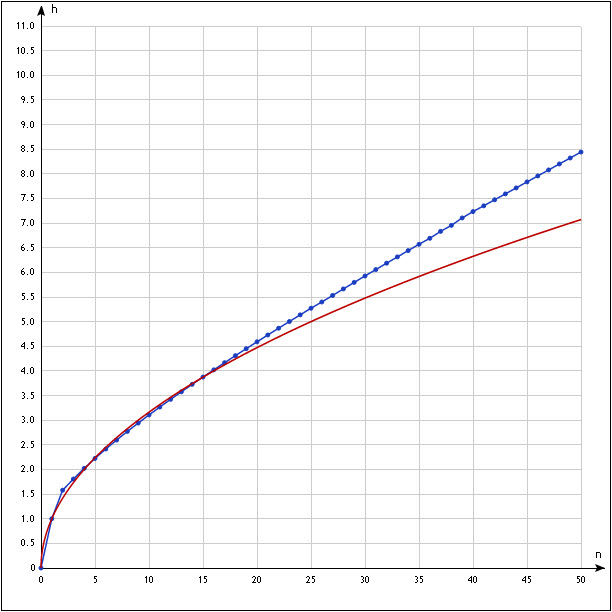
рисунок 3

Анализ изображений с помощью искусственных нейронных сетей

 Михалёв Артур Вячеславович,

ученик 11-а класса МОУ «Бендерский теоретический лицей»

Руководитель: Тереханова Ирина Владимировна, учитель информатики и ИКТ МОУ «Бендерский теоретический лицей»

Целью работы является сравнение возможностей искусственных нейронных сетей различных конфигураций в области распознавания изображений (цифр и знаков).

Для достижения цели были поставлены следующие задачи: изучить литературу по теме исследования, изучить язык программирования Python и математические библиоетки для него, смоделировать работу искусственной нейронной сети прямого распространения, оценить точность распознавания объектов на изображениях

Для достижения поставленных целей был проведен анализ литературы, поставлен вычислительный эксперимент. 

Машинное обучение и методы искусственного интеллекта в последние годы приобретает всё большее распространение. Работа посвящена изучению возможностей применения нейронных сетей (ИНС) как одного из методов машинного обучения для распознавания графических объектов. В результате была разработана компьютерная программа на языке программирования Python для моделирования ИНС прямого распространения. Сеть показала хорошие результаты при распознавании рукописных цифр и меток. Нейронные сети — исключительно мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости.

Список использованной литературы

1. Хайкин С. Нейронные сети: полный курс. — М. Вильямс, 2008.
2. Комарцова Л. Г., Максимов А. В. Нейрокомпьютеры. — М. Изд-во МГТУ им. Н. Э. Баумана, 2004.
3. Золотых Н. Ю. Как обучаются машины?
4. Бизли Д. Python. Подробный справочник. — М. Символ-плюс, 2010.
5. http://keras.io — Официальный сайт библиотеки Keras.
6. http://python.org — Официальный сайт языка Python.

В математической литературе много внимания уделяется внутренним точкам выпуклых многоугольников, для  которых сумма расстояний до сторон или до вершин данного многоугольника является наибольшей или наименьшей. Обычно наличие таких точек называют «экстремальными» свойствами выпуклых многоугольников, а сами такие точки называют «экстремальными».

Работа посвящена исследованию экстремальных свойств внутренних точек выпуклых многоугольников и многогранников. Предметом исследования стали наибольшие и наименьшие значения среднего арифметического, среднего геометрического, среднего гармонического и среднего квадратичного расстояний от внутренних точек выпуклого многоугольника до его сторон, а также от внутренних точек выпуклого многогранника до его граней.

Автором самостоятельно найдено наибольшее значение среднего геометрического, наименьшее значение среднего квадратичного и наибольшее значение среднего гармонического расстояний от внутренней точки выпуклого многоугольника до всех его сторон. В качестве следствий получены экстремальные свойства некоторых замечательных точек треугольника таких, как центроид, точка Лемуана а также точки, названной автором точкой гармонии треугольника.  Найдено наибольшее значение среднего геометрического, наименьшее значение среднего квадратичного и наибольшее значение среднего гармонического расстояний от внутренней точки выпуклого многогранника до всех его граней. В качестве следствия получено экстремальное свойство центроида тетраэдра. Полученные результаты исследования не встречались в математической литературе.

Знание экстремальных свойств некоторых внутренних точек выпуклых многоугольников и многогранников упрощает решение многих задач геометрии,  открывает широкие возможности для дальнейшей исследовательской деятельности, устанавливает тесные предметные связи между алгеброй и геометрией.

Всем нам трудно иногда посчитать двузначые или трёхзначные числа. Мы стоим по 3 часа и думаем, как умножить или разделить то или иное число или мы берём листок бумаги и решаем пример столбиком. Мне пок ахалось интересным узнать, существуют ли формулы для счёта чисел в уме. Именно о них я хочу рассказать!

Данная работа посвящена металлическим пропорциям, в частности серебряному. Числа Пелля (которые определяются с помощью серебряной пропорции) плохо изучены на практике, однако в теории настолько многообещающие, что готовы «соперничать» с числами Фибоначчи. Возможно пройдет еще пару десятилетий, прежде чем мы начнем их использовать в промышленности и естествознании, но они наверняка изменят наше представление о законах природы. Эта работа ставит перед собой задачу разобраться с значением Чисел Пелля и их особенностями.

В своей работе я решил изучить влияние разных антибиотиков и антисептиков на бактерии.

ЧАСТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДОПОЛНИТЕЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ "1С-ОБРАЗОВАНИЕ"

г. Москва

ПРОГРАММА ДЛЯ ЗАЩИТЫ ИНФОРМАЦИИ

CSSDATA

Автор: Большим Максим Антонович

Ученик 10 «Б» класса МБОУ СОШ № 30 г. Подольска

Научный руководитель: Чемисов Сергей Андреевич

Преподаватель ЧОУ ДПО "1С-ОБРАЗОВАНИЕ"

1. Цель проекта:

Создать программу, защищающую информацию (текстовые документы, медиафайлы, приложения и т.д.) от несанкционированного доступа с помощью применения методов криптографии и стеганографии.

Сделать программу доступной для работы неопытным пользователям и пригодной для работы специалистам в области защиты информации.

Предоставить пользователям инструмент для обеспечения безопасности важных для него данных.

2. Актуальность:

С развитием информационных технологий, всё большую актуальность приобретает понятие защиты информации от несанкционированного доступа. Постоянная слежка и новости о взломах различных систем вынуждают задуматься о недоступности информации любого рода и характера для чужих лиц. Программа CSSData создана для решения этой проблемы.

3. Описание:

CSSData- кроссплатформенная программа, созданная на языке Java.

Она представляет собой механизм, объединяющий воедино программы, реализующие методы криптографии стеганографии. При запуске пользователю доступен интуитивно понятный интерфейс, где он сразу может начать работу. В отличие от множества других программ и интернет сервисов программа предоставляет огромное кол-во настроек и методов защиты информации. В разделе криптографии пользователю предоставляется возможность выбрать известные алгоритмы шифрования(AES, BlowFish, DES, Triple DES, RC2, RC4, RSA), настроить длину ключа, IV вектор, режим шифрования, дополнения для блочного типа шифрования и, разумеется, пароль. В разделе стеганографии пользователю предоставляется скрыть два типа информации(файл, текст) в медиафайлах двумя способами: скрыть файл, предварительно зашифровав его; скрыть без шифрования. В конце каждой операции в программе предлагается отправить файл на email пользователя.

4. Задачи:

1) Изучить основы криптографии. Изучить понятия: симметричное, асимметричное, блочные и поточные алгоритмы шифрования; режимы блочного шифрования; хеширование.

2) Изучить основы стеганографии. Изучить LSB метод скрытия данных. Научиться манипулировать с информацией на битовом уровне.

3) Выбрать язык программирования и необходимые библиотеки для реализации проекта.

4) Реализовать механизмы работы стеганографии и криптографии в программе и связать их с удобным для восприятия интерфейсом.

5. Инструменты для реализации:

1) Для разработки проекта выбран язык Java, из-за кроссплатформенности и наличия расширенного кол-ва требуемых библиотек;

2) Для работы с медиафайлами выбрана библиотека Xuggler из-за огромного функционала, большого кол-ва поддерживаемых кодеков и высокоуровневого API;

3) Для отправки сообщений на email выбрана библиотека Mail;

4) Для предотвращения запуска большого количества копий программы, во избежание замедления работы задействована библиотека JNA.

5) Для реализации методов криптографии я использовал встроенные инструменты шифрования Java из библиотеки JCE.

6. Алгоритмы работы:

Как было сказанно выше, программа представляет собой механизм, объединяющий воедино программы, которые выполняют основные задачи.

Таких программ всего две: программа, реализующая методы криптографии; программа, реализующая методы стеганографии.

В свою очередь эти программы состоят из нескольких методов(алгоритмов):

1. Программа криптографии состоит из 2 алгоритмов: шифровка или расшифровка файла и шифровка или расшифровка текста;
2. Программа стеганографии состоит из 1 алгоритма: внедрение или извлечение файла или текста;

Так же в программе существует два протокола шифрования файла: простое шифрование(подходит для взаимодействия с другими программами шифрования) и шифрование с преобразованием(подойдет только простым пользователям, но при этом несколько увеличивается криптостойкость шифруемого файла).

Шифрования с преобразованием было специально создано для простых пользователей. Суть в том, что при дешифровании в программе пользователю достаточно знать алгоритм шифрования, длину ключа, пароль и все. Остальные программы шифрования расшифровать файл этот не смогут. Взломщику будет гораздо сложнее расшифровать файл. Протокол простого шифрования альтернативен протоколу шифрования текста. Этот режим требует знание абсолютно всех настроек, что были введены при шифровании. При расшифровке текста так же нужно знать все настройки. Чтобы пользователь мог не беспокоиться о том, что он может забыть эти настройки, после совершения операции предлагается сохранить параметры шифрования на компьютере и отправить их потом на email пользователя.

Блок-схемы криптографических протоколов находятся в прикрепленном тезисе.

В программе стеганографии я реализовывал LSB метод(замена последних значащих битов в контейнере на биты скрываемого сообщения) для изображений и аудио. Поддержка LSB стеганографии видеофайлов будет добавлена в следующих версиях программы.

7. Новизна:

В интернете не существует программы, выполняющей такой широкий спектр действий для защиты информации. Отдельно существующие сервисы шифрования не предоставляют детальных настроек шифрования и не способны справляться с большими файлами быстро, а сервисы стеганографии иногда не могут должным образом скрыть информацию или извлечь её. Новизна CSSData заключается в том, что:

1) Она быстро и надежно шифрует и скрывает информацию;

2) Не ограничена объёмами обрабатываемой информации;

3) Доступна в работе как специалистам, так и неопытным пользователям.

8. Планы развития:

В ближайшем будущем предполагается сделать WEB версию CSSData, что должно сделать программу доступной всем и одной из самых лучших в рунете. Так же планируется добавление новых возможностей, криптографических алгоритмов, видео-стеганографию, исправление ошибок. Пользователь с помощью данной программы может защитить любую информацию. Примером может стать:

          1) Информация, связанная с денежными средствами;

          2) Личные данные;

          3) Секретная для посторонних лиц информация.

9. Итог:

Изучены основы областей криптографии и стеганографии. Изучены принципы работ некоторых алгоритмов шифрования, строения аудио-файлов и изображений, законы логики для манипуляции битами. Проект успешно создан и в скором времени начнется разработка интернет-клона этой программы. Программа отлично справляется с шифрованием многогигабайтовых файлов и скрытием файлов в контейнере без повреждений. 

10. Используемые интернет-ресурсы и литература:

К. Хорстманн «Java: Библиотека профессионала» 9-е издание, г. Москва, 2016 г.;

Г. Вадим «Цифровая стеганография», 2002 г.;

Citforum.ru – Режимы шифрования –

 http://citforum.ru/security/cryptography/rejim_shifrov/ - [интернет-ресурс, дата последнего обращения – 17.12.2016 г.];

Java.com - Java Cryptography Architecture Sun Providers Documentation - https://docs.oracle.com/javase/8/docs/technotes/guides/security/SunProviders.html -

[интернет-ресурс, дата последнего обращения – 17.12.2016 г.];

Dreamincode.net – Steganography – http://www.dreamincode.net/forums/topic/27950-steganography/  - интернет-ресурс, дата последнего обращения – 15.10.2016 г.];

Javacodegeeks.com - Xuggler Tutorial: transcoding and media change - https://www.javacodegeeks.com/2011/02/xuggler-tutorial-transcoding-media.html - [интернет-ресурс, дата последнего обращения – 20.10.2016 г.];

Википедия – свободная энциклопедия -  http://ru.wikipedia.org/ - [интернет-ресурс, дата последнего обращения – 21.12.2016 г.];

StackOverFlow – Форум  программистов - http://stackoverflow.com - [интернет-ресурс, дата последнего обращения – 25.12.2016 г.];

CyberForum - Форум  программистов и сисадминов - http://www.cyberforum.ru - [интернет-ресурс, дата последнего обращения – 21.11.2016 г.];

Xuggler.com – Xuggler documentation - http://www.xuggle.com/public/documentation/java/api/ - [интернет-ресурс, дата последнего обращения – 15.11.2016 г.];

Oracle.com - Java™ Platform, Standard Edition 8 API Specification - http://docs.oracle.com/javase/8/docs/api/ - [интернет-ресурс, дата последнего обращения – 16.12.2016 г.].

Математическое моделирование движения человека при исполнении прыжков в фигурном катании на примере прыжка тур

Лядова Елизавета Александровна

МБОУ "Лицей №1" г. Перми

Шабрыкина Наталья Сергеевна, к. ф.-м. н., доцент ПНИПУ

Анферов Сергей Дмитриевич, старший преподаватель ПНИПУ

Цели и задачи:

Данная работа посвящена математическому моделированию движения спортсмена при исполнении прыжка тур в фигурном катании. Целью работы является выявление зависимости параметров прыжка (угловой скорости вращения в полете, количества совершенных оборотов) от движения корпуса и рук спортсмена во время подготовки к прыжку, отталкивания и полета. Задачи, которые необходимо решить для достижения цели: построение математической модели движения человека при исполнении прыжка тур; разработка системы захвата движения; разработка методики и проведение эксперимента для получения необходимых при моделировании величин.

Актуальность и новизна исследования:

От сложности и чистоты исполнения прыжков в фигурном катании во многом зависит итоговая оценка выступления фигуриста. На конечный результат влияет большое количество параметров, поэтому часто даже опытные тренеры не могут определить причину возникновения ошибок при исполнении прыжков. Несмотря на это, в научной литературе очень мало работ, посвященных исследованию этой темы. Непосредственно математические модели элементов фигурного катания имеются в работах только двух авторов [2-3]. В отличие от  вышеупомянутых авторов, в данной работе рассматривается комплексная модель, учитывающая взаимосвязь разных этапов выполнения прыжка, и проводятся эксперименты для идентификации и верификации предложенной модели. Результаты данной работы в дальнейшем будут использованы для построения комплексной модели прыжка в фигурном катании, которая сможет помочь спортсменам при освоении новых прыжков, а также при выявлении причин ошибок в исполнении уже изученных многооборотных прыжков.

Описание исследовательской работы:

В работе строится математическая модель прыжка тур. Тур – это прыжок на полу с места с двух ног вертикально вверх, приземление производится на две ноги или в позицию выезда. Для описания движения тела фигуриста в ходе выполнения прыжка тур используется модель человека, состоящая из следующих частей: шара (голова), усеченного конуса (корпус), усеченного конуса (ноги) и четырех стержней (плечо и предплечье правой и левой руки). Угловая скорость вращения фигуриста в полете определяется с помощью теоремы об изменении кинетического момента. Были выведены формулы для нахождения кинетического момента, приобретенного фигуристом при отталкивании за счет скручивания корпуса, и момента инерции тела фигуриста в фазе полета. Для описания движения рук и корпуса в фазах отталкивания и полета необходимо знать положение рук и корпуса в любой момент времени. Поскольку соответствующих экспериментальных данных в литературе не найдено, для определения всех необходимых величин были проведены собственные эксперименты. Для получения необходимых данных была разработана система двумерного захвата движения, включающая в себя набор маркеров с системой крепления и программный комплекс для обработки данных видеосъемки.

Итоги исследования:

В данной работе построена математическая модель прыжка тур, включающая в себя модель закручивания корпуса при отталкивании и модель вращения в воздухе в фазе полета. Для определения положения корпуса и рук фигуриста в ходе выполнения прыжка разработана двумерная система захвата движения: изготовлен набор маркеров с системой крепления (рис.1 а), создан программный комплекс для обработки данных видеосъемки (рис.1 б). Разработана методика проведения эксперимента по исследованию прыжка тур, проведена серия экспериментов с участием фигуриста-любителя. С помощью математической модели и полученных из эксперимента данных о положении частей тела фигуриста при исполнении прыжка, определена угловая скорость фигуриста в фазе полета (рис.2 б) и вычислены момент инерции тела фигуриста в фазе полета (рис.2 а) и  количество оборотов, совершаемых в прыжке. Сделаны предварительные выводы об адекватности предложенной модели.

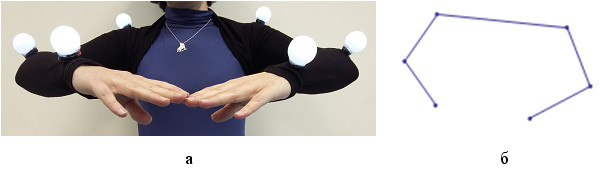
Рис. 1. Внешний вид маркеров (а) и результат обработки видео (б).

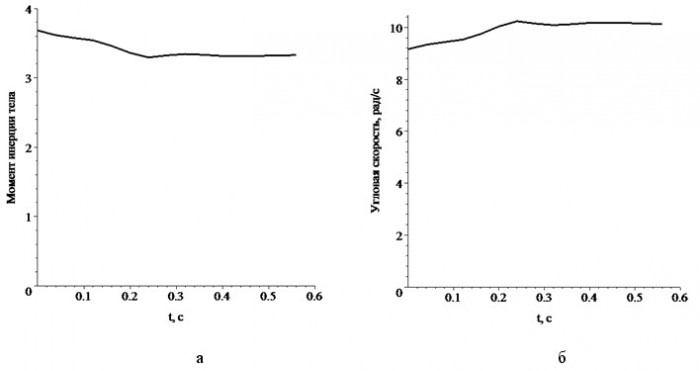
Рис. 2. Изменение момента инерции тела фигуриста (а) и угловой скорости вращения вокруг оси (б) в ходе выполнения прыжка.

Список использованной литературы:

1. Фигурное катание. https://ru.wikipedia.org/wiki/Фигурное_катание.
2. King D. Performing Triple & Quadruple Figure Skating Jumps: Implications for Training // Canadian Journal of Exercise Physiology. – 2005. – № 30(6). – P. 743-753.
3. King D. Generation of Vertical Velocity in Toe-Pick Figure Skating Jumps // Proc. of 19 International Symposium on Biomechanics in Sports, San Francisco. – 2001. – P. 66-69.
4. Kepple T., Trager S., Mattson J., Richards J. Computer Simulation of the Flight Phase of Figure Skating Jumps // Proc. of Iutam Symposium on Human Movement Analysis and Simulation. Iutam. – 2010. – P. 123-125.
5. Kho E. Bone-on-Bone Forces at the Ankle and Knee in Figure Skaters during Loop Jumps: Clinical Implications // A thesis for the degree of Master of Science in Kinesiology. Waterloo, Canada, 1996. – 152 p.
6. Bruening D.A., Richards J.G. Individual Landing Strategies in Figure Skating Jumps // Annual Meeting of the American Society of Biomechanics. Virginia Tech, Blacksburg. – 2006. – P. 210-212.
7. Мишин А.Н. Биомеханика движений фигуриста. – М: Физкультура и спорт, 1981. – 144 c.
8. Мишин А.Н. Прыжки в фигурном катании. – М: Физкультура и спорт, 1976. – 107 c.
9. Виноградова В.И. Основы биомеханики прыжков в фигурном катании на коньках. – М.: Советский спорт, 2013. – 216 с.
10. Яблонский А. А., Никифорова В. М. Курс теоретической механики: Статика. Кинематика. Динамика: Учебное пособие для вузов. – М.: Кронус, 2010. – 608 с.
11. Захват движения, https://ru.wikipedia.org/wiki/Захват_Движения.
12. Борзиков В.В., Рукина Н.Н., Воробьева О.В., Кузнецов А.Н., Белова А.Н. Видеоанализ движений человека в клинической практике (обзор) // СТМ. – 2015. – Т. 7, №4. – C. 201-210.
13. Скворцов Д.В. Методика исследования кинематики движений и современные стандарты. Видеоанализ // Лечебная физкультура и спортивная медицина. – 2012. – № 12 (108). С. 4-10.
14. Wu G. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion – Part II: shoulder, elbow, wrist and hand / Wu G., van der Helm F.C., Veeger H.E., Makhsous M., Van Roy P., Anglin C., Nagels J., Karduna A.R., McQuade K., Wang X., Werner F.W., Buchholz B. // Journal of Biomechanics. – 2005, 38(5). – P. 981-992.

Как -то раз , взяв учебник 10-11 класса "Геометрия "И.М .Смирнова , я обратил внимание , на рисунок , размещённый на обложке .Это был куб с полосками .Выступы на лентах являются визуальным ориентиров того, как расположены полоски в пространстве и как они переплетаются с кубом.И если верите своим глазам , то вы никогда не поверите тому, что нарисовано на этой картине.В каждой главе пресутвуют рисунки с изображением пространственных фигур , с различным способом их моделирования.Я задался вопрос , кто автор этих рисунков , какой математик ? И почему эти картины так и манят к себе, так притягивают? А это потому , что в ней чувствтвуется гармония.

Оказывается, эти пространственные фигуры изобрёл Эшер , после я начал больше интересоваться фигурами в пространстве и вот что я узнал.Каждая работа Эшера это загадка .Можно часами рассматривать его графику , мазунку , пейзажи сферы и другие обЪекты .Даже его пейзади-это головоломки интересным решением . От его работ не возможно устать, вель вам престоит постоянно открывать для себя новые, не замеченные ранее, штрихи.Графика Эшера поражает тем , что в ней нет ничего невозможного.В процессе своей работы он черпал идеи из математических статей , в которх рассказывалось о мозаичном разбиении плоскости, проецировании трёхкамерных фигур на плоскость и неевклидовой геометрии. Он был очарован всевозможными парадоксами в том чесле "невозможными фигурами "Наоболее интересными для изучения идеями Эшера являются всевозможные разбиваня плоскости и логика трехмерного пространства .

Цель:

Создать приложение для операционных систем Android и Windows, позволяющее передавать данные с одного устройства на другое  через беспроводную локальную сеть.

Реализация:

С помощью Java и С# создать программу для двух платформ.Загрузить приложение для общего доступа в Play Маркет и Windows Store.

Демонстрация работы программы(версия с использованием FTP):

 Многогранники привлекали внимание математиков со времен античности. Однако тема до сих пор не исчерпала себя. Так, во второй половине XX столетия абстрактная теория многогранников оформилась в самостоятельный раздел математики.

 Проект посвящен исследованию разбиения выпуклых многогранников на тетраэдры. Рассмотрены вопросы: о минимальном количестве тетраэдров, на которые могут разрезаны многогранники, относящиеся к определенным классам; о всех возможных количествах тетраэдров при использовании разрезания специального вида, являющегося естественным обобщением триангуляции многоугольников диагоналями.

В работе предложен новый подход к классификации выпуклых многогранников, опирающийся на специальный, но вполне естественный способ разбиения многогранников на тетраэдры. Полностью описаны классы многогранников с небольшим количеством рёбер.

Создание единой системы мониторинга ("Умной диспетчерской") - системы слежения за сигналами датчиков электронных систем "Умного города" на основе 3-d модели. Модель города  разработана в MaxonCinema 4DStudioR16.  Обработка сигналов реализована с помощью сети светодиодов, соединённых в электрическую сеть, проложенную через здания макета города.  Для автоматизации модели использован Arduino MEGA 2560.

Подробно о ходе работы и результатах в приложенном файле.

тезисы

Тема: Способы решения нелинейных уравнений

Научный руководитель: Симакова М.Н. Симаков Е.А.

В работе представлены некоторые способы решения уравнений различными способами, в том числе при помощи ЭВМ

Актуальность выбранной темы заключается в том, что без математической грамотности невозможно успешное освоение методов решения задач по физике, химии, биологии и другим предметам. Весь комплекс естественных наук построен и развивается на базе математических знаний. Например, исследование ряда актуальных задач математической физики приводит к необходимости решения нелинейных уравнений. Построение решения таких уравнений эффективными способами  является важной и актуальной задачей. Решение нелинейных уравнений необходимо в нелинейной оптике, физике плазмы, теории сверхпроводимости и физике низких температур. По этой теме есть достаточное количество литературы, но во многих учебниках и статьях трудно разобраться ученику средней школы. В данной работе рассмотрены методы решения нелинейных уравнений, которые можно использовать при решении прикладных задач физики, химии уже в школе. Интересным представляется аспект применения информационных технологий к решению уравнений и задач по математике. Это, с одной стороны, способствует расширению и углублению математических знаний, привитию интереса к математике. Данная тема важна и при дальнейшем получении высшего образования.

Цель работы: изучение методов решения нелинейных уравнений с одним неизвестным при помощи некоторых методов

1.Шаговый метод

2Метод половинного деления

3Метод Ньютона

4  PTC Mathcad

Гипотеза: методы решения нелинейных уравнений имеют свои достоинства и недостатки, рациональность их применения зависит от условий данного уравнения

Перейдем к знакомству с указанными методами. Сначала позвольте сказать общие сведенья о решении нелинейных уравнений

Рассмотрим общий алгоритм решения численными методами

Шаговый метод:

Имеет очень важное достоинство – простота алгоритма решения. Недостаток метода заключается в том что для большей точности результата необходимо существенно уменьшит размер шага, а это существенно увеличит время рассчета

Алгоритм решения

Этап отделения корней.
На этом этапе мы определяем участки, на каждом из которых лежит только один корень уравнения. Есть несколько вариантов реализации этого этапа:

• Вариант 1. Подставляем значения X (желательно с каким-то достаточно мелким шагом) и смотрим где функция сменит знак. Если функция сменила знак, это значит, что на участке между предыдущим и текущим значением X лежит корень (если функция не меняет характер возрастания/убывания, то можно утверждать, что корень на этом интервале один).
• Вариант 2. Графический метод. Строим график и оцениваем на каких интервалах лежит один корень
• Вариант 3. Используем свойства конкретной функции.

Этап уточнения корней

• Вариант 1. Метод половинного деления.
• Вариант 2. Метод Ньютона.

Метод половинного деления

Достоинство метода – быстрая сходимость т.к. при каждом действии интервал сужается в 2 раза. Главный недостаток заключается в том, что если на заданном интервале содержится более одного корня, то метод не работает.

Алгоритм

• Определить новое приближение корня х в середине отрезка [а;b]: х=(а+b)/2.
• Найти значения функции в точках а и х: F(a) и F(x).
• Проверить условие F(a)*F(x) < 0. Если условие выполнено, то корень расположен на отрезке [а;х]. В этом случае необходимо точку b переместить в точку х (b=х). Если условие не выполнено, то корень расположен на отрезке [х;b]. В этом случае необходимо точку а переместить в точку х (а=х).
• Перейти к пункту 1 и вновь поделить отрезок пополам.
• Алгоритм продолжать до достижения необходимой точности

Метод Ньютона

Достоинство метода заключается в том, что он подходит для решения очень сложных уравнений, без изменений обобщается на комплексный случай. Недостаток метода – необходимость вычисления производных на каждом шаге

Рассмотрение алгоритма на конкретном примере

Пусть нам дана возрастающая функция y = f(x) =x²-2, непрерывная на отрезке (0;2), и имеющая f '(x) = 2x > 0 и f ''(x) = 2 > 0.

• Уравнение касательной имеет вид: y-y₀=2x₀·(x-x₀). В качестве точки x₀ выбираем точку B₁(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B₁, и обозначаем точку пересечения касательной и оси Ox точкой x₁. Получаем уравнение первой касательной: y=4x-6.
• Точка пересечения касательной и оси Ox: x₁ =6/4=1.5
• Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₁, получаем точку В₂ =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В₂, и обозначаем точку пересечения касательной и оси Ox точкой x₂.
• Уравнение второй касательной: y = 3x – 4.25.
• Точка пересечения касательной и оси Ox: x₂ = 4.25/3
• Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₂, получаем точку В₃ и так далее.
• В3 = (4.25/3;(4.25/3)^2)
• Первое приближение корня определяется по формуле:

                                               x1=x0-f(x0)/f'(x0)   = 1.5.

• Второе приближение корня определяется по формуле:

                                               x2=x1-f(x1)/f'(x1)   =1.416.

             Третье приближение корня определяется по формуле:                                                                                        x3=x2-f(x2)/f'(x2)   = 1.414215.

• Таким образом, i-ое приближение корня определяется по формуле:                                                                  xi=xi-1-f(xi-1)/f'(xi-1)   
• Вычисления ведутся до тех пор, пока не будет достигнута заданная точность
• В нашем случае, сравним приближение, полученное на третьем шаге с реальным ответом, посчитанном на калькуляторе

 /2=1,414213

 x3=1.414215

Решение уравнения при помощи САПР MathCAD

Для решения простейших уравнений при известном начальном приближении целесообразно использовать ROOT

Если начальное приближение неизвестно или необходимо найти все корни уравнения используется SOLVE

В ходе исследования по теме «Методы решения нелинейных уравнений» рассмотрены как математические методы, так и решение уравнений с использованием программирования, САПР MathCAD. Различные методы имеют свои достоинства и недостатки. Следует отметить, что применение того или иного метода зависит от начальных условий заданного уравнения. Те уравнения, которые хорошо решаются известными в школе методами разложения на множители и т.п., не имеет смысла решать более сложными способами. Прикладные задачи математики, важные для физики, химии и требующие сложных вычислительных операций при решении уравнений успешно решаются, например, с помощью программирования. Их же хорошо решать методом Ньютона.

Для уточнения корней можно применять несколько методов решения одного и того же уравнения. Именно это исследование и легло в основу данной работы. При этом легко проследить, какой метод наиболее удачен при решении каждого этапа уравнения, а какой метод на данном этапе лучше не применять.

Изученный материал, с одной стороны, способствует расширению и углублению математических знаний, привитию интереса к математике. С другой стороны, задачи реальной математики важно уметь решать тем, кто собирается приобрести профессии технического и инженерного направления. Поэтому данная работа имеет значение для дальнейшего образования (например, в высшем учебном заведении).

Представленная работа посвящена одному из важнейших преобразований планиметрии – гомотетии. В исследовании изложены теоретические основы по данному преобразованию, а также приведен ряд задач, где использование преобразований подобия в качестве основного инструмента, позволяет получать краткие и изящные решения.

Актуальность работы, обусловлена тем, что в школьной программе этому разделу геометрии отведено совсем немного времени, несмотря на возможности, которые предоставляет использование метода гомотетии в решении ряда задач.

В связи с этим целью разработки стало расшириние знаний по этой теме и разработка методического материала, способного иллюстрировать это преобразование в процессе обучения решению геометрических задач.

Задачами работы было изучение и подбор теоретического материала, а также поиск решения геометрических задач с помощью изучаемого метода.

В работе представлены 3 раздела: «Свойства гомотетии», «Композиции гомотетий» и «Поворотная гомотетия» .Теоретические сведения предваряют практическую часть. В представленном материале основное внимание сосредоточено на практической части. Приведенные в данной работе задачи являются заданиями математических олимпиад, либо известными классическими примерами из планиметрии, такими как прямая Эйлера, окружность девяти точек, теорема Фейербаха, точка Микеля, лемма Веррьера.

Работа содержит весь материал, касающийся преобразований подобия, за исключением классификации преобразований подобия, системы движущихся подобных фигур и задач на построение. Эти разделы опущены с целью минимизации объема материала. В работе, также, приведено новое решение известной теоремы Фейербаха.

В результате проделанной работы удалось подготовить методический материал, по преобразованиям подобия, способный оказать существенную помощь при изучении геометрии, а использование представленных решений может быть не только интересно, но и полезно, как преподавателям, так и любителям геометрии, изучающим этот раздел планиметрии.

Математика в биоинформатике: как собирают геном

Шамаев С.А., Павлов Л.Е.

Россия, Липецкая область, г. Липецк

Лицей № 44 города Липецка, ГОБОУ «Центр поддержки одаренных детей», 5 класс

Научный руководитель: к.т.н., доц.кафедры прикладной математики Липецкого государственного технического университета Шуйкова И.А.

Целью работы является изучение графов де Брейна и иллюстрация с их помощью решения задачи биоинформатики «сборка генома».

Методы, используемые в работе: в работе используются методы комбинаторики для анализа исследуемых объектов, начальные знания по теории графов, методы оперирования с простейшими геометрическими фигурами.

В ходе исследования были поставлены и решены следующие задачи работы:

1. изучение литературы и видеоматериалов по теме исследования: – изучение истории развития биоинформатики; – изучение модели представления ДНК как строки для компьютерной обработки; – знакомство с графами де Брейна; ‑ изучение алгоритмов построения строки, включающей в себя заданные подстроки.
2. проведение серии практических работ по исследованию алгоритма построения строки, включающей в себя заданные подстроки.
3. выполнения учебной работы по «сборке генома».

Основной текст тезисов

Исследовательская работа является продолжением практического исследования, начатого авторами в младшей школе. Первый год работы был посвящен проблеме четырех красок. Мы, как и математики, начали с проверки утверждения четырех красок для различных карт, раскрашивая их. Затем, мы изучили жадный алгоритм раскраски вершин графов, при помощи которого теперь мы можем расскрашивать графы. Работа по данной теме была доложена в 2016 года на конференции «Старт в науку» МФТИ. Прикладное значение алгоритмов раскраски графов довольно широко и, в частности, одной из современных и развивающихся в настоящее время областей приложения данного алгоритма является бионформатика. Биоинформатика использует математические методы и компьютерные алгоритмы для решения биологических задач. Задача этого исследования заключалась в использовании графов для моделирования задачи сборки генома. В следующем исследовании мы надеемся изучить применение алгоритма раскраски вершин графа в задачах биоинформатики.

Для описания ДНК в виде нуклеотидной последовательности (последовательности символов) применяют секвенирование. Секвенирование производят при помощи секвенаторов – специальной аппаратуры и технологий. Но геномные секвенаторы в настоящее время еще не могут получить полную последовательность ДНК. Вместо длинных фрагментов получают много коротких фрагментов. Задача биоинформатиков заключается в том, чтобы по данным коротким фрагментам получить одну длинную цепочку ДНК. Мы сделали учебный пример сборки генома, используя двоичный алфавит и тримеры (трехбитовый слова, составленные из 0 и 1) на графах де Брейна при помощи поиска гамильтонова и эйлерова цикла в графе.

Итогом исследования является применение алгоритма поиска эйлерова цикла к графам де брейна для поиска циклическое двоичной последовательности наименьшей длины, составленной из фрагментов – двоичных тримеров.

Исследование опирается на следующие библиографические источники:

1. Артем Касьянов: "Как собрать геном из миллиарда кусочков? Компьютеры и современная биология." [Электронный ресурс]. Режим доступа: https://www.youtube.com/watch?v=kq2D2ucX6qI
2. Александр Омельченко. Граф де Брейна. Курс «Основы теории графов» [Электронный ресурс]. Режим доступа: https://stepik.org
3. Алгоритмы в биоинформатике. [Электронный ресурс]. Режим доступа: Лекция 1. https://www.lektorium.tv/lecture/14229

Название работы: Возможность представления алгебраической дробив виде суммы дробей заданной последовательностью

Автор работы: Плотников Иван Дмитриевич

Место обучения: МБОУ г.Магадана «СОШ с УИМ №15»

Научный руководитель: Евсютина Татьяна Хамидовна

Должность научного руководителя: учитель математики

Место работы научного руководителя: МБОУ г.Магадана «СОШ с УИМ №15»

Тема моего доклада: возможность представления алгебраической дроби в виде суммы дробей заданной последовательностью.

Цель работы:

1)Применение метода математической индукции при решении задач на доказательство суммы членов последовательности.

2)нахождение формулы суммы членов последовательности

3)нахождение формулы последовательности при известной формуле суммы

4)подведение итогов

Сперва несколько слов о методе математической индукции:

            Метод математической индукции используется для доказательства утверждений, зависящих от натурального аргумента. Для доказательства утверждения методом математической индукции необходимо:

• проверить справедливость для первого натурального числа, для которого доказывается утверждение.
• В предположении, что утверждение верно для натурального числа n=k, доказать справедливость утверждения для следующего натурального числа n=k+1.

Актуальность данной темы заключается в следующем: в школьном курсе тема «Последовательности» изучается сравнительно недолго, исключив изучение суммирование членов последовательности произвольного вида, хотя решение задач такого типа позволяет развивать логику и математическую интуицию.

Новизна исследования заключается в том, что в процессе решения заданий мною была получена информация о принципе их составления. Эта работа позволила осознать принцип решения заданий как в прямом направлении, так и в обратном.

Итог: мою работу можно использовать при подготовке абитуриентов к поступлению в ВУЗы, на факультативах и элективах. Мне это пригодится при дальнейшем обучении.

При описании течения жидкости в нефтеносных пластах часто используются функции комплексного переменного.

В работе получено описание линий тока жидкости от трещины, образуемой в результате гидроразрыва пласта.

Рассмотрены различные виды трещин. Для решения поставленных задач изучаются некоторые функции (степенная, функция Жуковского).

Описываются свойства функции Жуковского. Показано, что при удалении от трещины течение жидкости фактически близко к радиальному. Для построения линий тока и линий равного давления использовалась система компьютерной математики Maple.

Исследовательский проект: "Криптография. Шифры перестановки."

Жогова Мария Сергеевна,

МАУ ДО ЦДО «Стратегия», МБОУ гимназия №12, 8 класс

Шуйкова Инесса Анатольевна, к.т.н., доцент кафедры прикладной математики ЛГТУ

Целью работы является создание программы, моделирующей работу шифровального устройства.

Задачи, необходимые для выполнения цели работы:

• Изучить теоретический материалы по теме исследования;
• Ознакомиться с основными методами шифрования;
• Создать программу, которая шифрует сообщение методом вертикальной перестановки;
• Создать программу, которая шифрует сообщение методом двойной перестановки;
• Изучить теоретический материалы по теме «взлом шифров»;

Актуальность работы: Необходимость защиты информации возникла задолго до появления информационных технологий, уже в те времена, когда с возникновением письменности появилась и опасность ознакомления с информацией лицами, которым она не предназначена. Первое время вопрос решался достаточно просто: умение читать и писать было уделом избранных.

Описание научно-исследовательской работы: 

В первой главе приведены основные понятия и определения, приведена классификация алгоритмов шифрования. Во второй главе рассказывается о видах перестановочных шифров. В третьей главе показана реализация некоторых видов шифров и представлен теоретический материал по теме «взлом шифров».

Выводы: Итак, в ходе выполнения работы была достигнута поставленная цель: была изучена теоретическая база криптографии; были освоены и реализованы несколько методов шифрования данных.

В процессе исследования были поставлены и решены следующие задачи: изучено применение основных методов шифрования в криптографии; исследована литература; написана программа, шифрующая данные несколькими методами шифрования.

Развитием работы будет дальнейшее изучение других алгоритмов криптографии, их комбинирование и реализация на практике.

Библиографический список:

• Н. Смарт – «Криптография» – Москва: Техносфера, 2005
• А.Ю.Зубов, А.В.Зязин, В.Н.Овчинников, С.М.Рамоданов – «Олимпиады по криптографии и математике для школьников» - Москва: Издательство МЦНМО 2006
• О. Н. Василенко – «Теоретико-числовые алгоритмы в криптографии» - Москва: МЦНМО, 2003
• Романьков В.А. – «Введение в криптографию. Курс лекций» – Москва: ФОРУМ, 2012
• Алферов А. П., Зубов А. Ю., Кузьмин А. С., Черемушкин А. В. – «Основы криптографии Учебное пособие», 2-е изд., испр. и доп. — М.. Гелиос АРВ, 2002.
• Н. Коблиц – «Курс теории чисел и криптографии» – Москва: Научное издательство ТВП, 2001
• Бабаш А.В., Шанкин Г.П. – «Криптография» – Москва: СОЛОНО-ПРЕСС, 2007
• https://habrahabr.ru

Данная работа показывает возможность использования программы AUDACITY для обработки звука и создания звуковых композиций. Подробно описан алгоритм работы, а в презентации представлен материал, который является теоретической основой для работы с программой. Результатом изучения программы явилось создание звуковых файлов, используемых для собственных нужд.

Тема работы "Проблема  глобального потепления и её связь с энергоэффективностью зданий и сооружений".Выполнила:Потехина А.А. Научный руководитель: Нафикова Е.В.

 «Использование JavaScript для расширения возможностей

разработки web-страниц»

Чурбанов Ростислав Юрьевич, 10 класс

МАОУ «Лицей №78 им. А.С. Пушкина»

г. Набережные Челны

Чурбанова  Ольга викторовна,

учитель информатики

МАОУ «Лицей №78 им. А.С. Пушкина»

Сегодня Интернет прочно занял нишу основного информационного поля школьников. Если раньше обращались за помощью в справочники и энциклопедии, то сейчас «Ok, google» ответит практически на все вопросы. Соответственно задача разработчиков сайта сделать так чтобы поиск нужной информации был быстр и точен. Как сделать наполненность страницы контентом максимальным и при этом не отпугнуть пользователя? В этом разработчику сайта может помочь язык JavaScript. Поэтому изучение данной темы актуально.

Изучение возможностей, которые дает JavaScript и проблемы, которые возникают при его использовании, вот основные моменты данного исследования. Объект исследования – язык JavaScript, а предметом исследования являются возможности язык JavaScript.

Цель работы – проанализировать возможности язык JavaScript и испытать их при разработке сайта «А.С. Пушкин. Аргументы».

Задачи работы:

• Изучить возможности язык JavaScript
• Опробовать их на практике
• Создать сайт «А.С. Пушкин. Аргументы» для реализации практической части и проведения экспериментов.

Гипотеза работы: ресурсы языка JavaScript расширяют возможности web-страниц.

При исследовании были использованы методы исследования экспериментально-теоретического уровня: эксперимент и анализ. Они помогли не только собрать теоретический материал по теме, но проверить их на практике, систематизировать.

Теоретическая значимость данной исследовательской работы заключается в изучении возможностей языка JavaScript и привлечения внимания к нему web-разработчиков.

Практическая значимость работы в создании сайта, полезного для выпускников школ, на котором можно продемонстрировать возможностей языка JavaScript.

Характеристика использованной литературы показала, что теоретического материала по этой теме много, хотелось опробовать его на практике.

Для реализации практической части был создан сайт «А.С. Пушкин. Аргументы» на языке разметки гипертекста HTML в текстовом редакторе Atom. Главная особенность Atom — богатые возможности по настройке. Редактор можно настроить на свой вкус. Изначально в него встроены файл-менеджер, продвинутые функции поиска и замены, разнообразные курсоры, опции сворачивания кода, ясный интерфейс.

Для оформления внешнего вида был использован язык CSS – каскадные таблицы стилей, так как он позволяет отделить описание внешнего вида сайта от его основного контента.

Для исследования возможностей JavaScript необходимо было найти оптимальный вариант добавления его на сайт. Существует два способа это сделать:

• Встроить JavaScript-код непосредственно в код страницы;
• Добавить JavaScript-код во внешний файл с расширение js.

Для эксперимента было решено использовать оба способа и сравнить результат. Итак, в результате встроенного сценария у нас получилось три папки: CSS, Fonts, Images и сама страница index.html. При внешнем сценарии у нас добавилась папка Js. Объем сайта сильно не изменился. В чем же разница:

• при внешнем сценарии HTML-файлы проще редактировать, они не перегружены строками JavaScript-кода,
• один и тот же JavaScript-код, как правило, используется на нескольких страницах. Если он будет оформлен внутри HTML-страницы, то для каждой страницы сайта его надо будет писать заново, а во внешнем сценарии один JavaScript-код может быть подключен несколько раз;
• внешний JavaScript-код загружается браузером всего один раз, при первом открытии страницы. Переходя на другие страницы сайта, где используется тот же код, он будет выводить его из кэша браузера, что в свою очередь сделает быстрее загрузку и обработку содержимого веб-страницы.

После определения способа подключения JavaScript-кода на сайт, началась работа над версткой сайта. Для улучшения дизайна и проверки возможностей JavaScript-код были использованы элементы шаблонов Bootstrap: Меню, кнопки, разметка страницы.

Для того чтобы страница стала более «живая» был добавлен JavaScript-код «Открытия книг» для перехода на другие страницы сайта.

Так же было решено с помощью JavaScript-код создать эффект «Обратной связи» для добавления аргументов пользователями сайта. Но в процессе реализации данной идеи стало понятно, что только с помощью JavaScript это реализовать невозможно. Сам процесс отправки аргумента реализован на РНР, а проверка правильности заполнения формы на JavaScript-коде.

Дальнейшей перспективой разработки сайта и демонстрации возможностей JavaScript будет добавление более сложных JavaScript-кодов.

В ходе выполнения работы были сделаны следующие выводы:

• JavaScript – это уникальная технология, позволяющая сделать сайт «живым», динамичным;
• Лучше использовать внешний сценарий встраивания JavaScript-кода;
• Для реализации связи сайта с сервером одного JavaScript-кода мало, без PHP это реализовать не удалось.

Итак, цели и задачи работы были достигнуты. На практике было доказано, что JavaScript действительно расширяет возможности разработки веб-страниц. Гипотеза работы доказана.

 Литература:

1. Гудман Д., Моррисон М., JavaScript. Библиотека пользователя. 5-е издание. –2006.
2. Колисниченко Д.Н. Современный сайт на РНР и JavaScript. –2009.
3. Крокфорд Д. JavaScript: сильные стороны. –2013.
4. Моррисон М. Изучаем JavaScript. –2012.
5. Никсон Р. Создаем динамические веб-сайты с помощью РНР, MySQL, JavaScript и –2013.
6. Уэнц К., JavaScript.Карманный справочник: – 2007.

Содержание

I. Что такое радиационный фон?
1.1. Из истории создания камеры Вильсона: прибор для регистрации заряженных частиц. Современные приборы для измерения радиации.
II. Основная. Экспериментальная.
2.1. Измерение радиационного фона на территории нашей школы.
2.2. Наблюдение и изучение корпускулярной составляющей радиационного фона.

Как считать различные ожерелья?

РКузнецов А., Титов Ф.

оссия, Липецкая область, г. Липецк

Гимназия № 12, школа № 55 города Липецка,

ГОБОУ «Центр поддержки одаренных де-тей», 6 класс, 5 класс

Научный руководитель: к.т.н., доц.кафедры прикладной математики Липецкого государственного технического университета Шуйкова И.А.

Целью работы является постановка и решение задачи «Как считать различ-ные ожерелья?»

Методы, используемые в работе: в работе используются методы наглядного оперирования объектами и наблюдения, методы комбинаторики для анализа ис-следуемых объектов.

В ходе исследования были поставлены и решены следующие задачи работы:

1. Постановка задачи «Как считать ожерелья?».

2. решение серии задач с разным количеством бусинок и цветов наглядно-практическим способом.

3. Написание компьютерной программы, позволяющей генерировать различные ожерелья из двух цветов и считать различные из них.

Основной текст тезисов

 Постановка задачи об ожерельях заключается в том, что нужно составить ожерелье из n бусинок различных цветов. Предварительно бусинки находятся в r коробках разных цветов (различные цвета и у коробок, в которых они лежат и у самих бусинок). Количество бусинок в каждой коробке неограниченно. Мы знаем, что всего в этом случае можно составить r^n ожерелий. Но среди них будут одина-ковые, то есть те, которые не отличаются друг от друга, если одно совместить с другим поворотом. Возникает вопрос – сколько же различных ожерелий получится.

Мы решили простейший вариант: r=2, n=3 задачи наглядно. Из бусинок двух цветов при длине ожерелья 3, можно составить 8 ожерелий: 000, 001, 010, 011, 100, 101, 110, 111. Но как видим, здесь всего 4 различных ожерелья: ( 000), (001, 010, 100), (011, 110, 101), (111). В работе также приведены другие конкретные примеры подсчета различных ожерелий. Написана программа, которая позволяет решать за-дачу перебором.

Рассмотрена вторая задача: подсчет количества различных слов длины l, ес-ли слова могут составлять из m букв и не различаются друг от друга, если у них совпадают крайняя левая и правые буквы. Задача также решена перебором и наглядно-практическим способом. В дальнейшем мы ставим перед собой задачу проанализировать полученные решения и сделать вывод о том, как они решаются методами комбинаторики.

Исследование опирается на следующие библиографические источники:

Задача об ожерельях, функция Мёбиуса и синхронизируемые коды.

//Электронный источник http://mathemlib.ru/books/item/f00/s00/z0000023/st040.shtml

Как считать различные ожерелья?

Титов Федор Александрович, Кузнецов Андрей Дмитриевич

Россия, Липецкая область, г. Липецк

МАУ ДО ЦДО «Стратегия», гимназия 12, школа 55,

Научный руководитель: к.т.н., доц.кафедры прикладной математики Липецкого государственного технического университета Шуйкова И.А.

Целью работы является изучение способов подсчета различных ожерельев, составленных из бусинок различных цветов.

В ходе исследования были поставлены и решены следующие задачи:

- формализована задача подсчета различных ожерельев;

- проведены вычисления для различного количества бус в ожерелье и двух цветов бусинок;

- написана программа, которая генерирует все двоичные последовательности заданной длины, по которым в дальнейшем можно группировать бусы в классы одинаковых бус.

Основной текст тезисов

Для подсчета возможного варианта расположения бусин в ожерелье рассматривается различное количество бусин и их цветов.

Пусть у нас имеется неограниченное количество бусин r цветов.

Необходимо подсчитать, сколько различных вариантов ожерелий, состоящих из n бусин можно сделать?  Различными будем считать те ожерелья, которые не совмещаются друг с другом при поворотах.

В приведенных примерах ведется подсчет для

n=8, r=3;   n=5, r=1; n=2, r=1; n=16, r=1

Для n=4, а r=2 у нас получилось 16 ожерельев, но некоторые из них совпали.

для примера n=5, r=2 у нас получилось 8 ожерельев.

Мы написали программу, которая при n = 5 и r = 2  генерирует и выводит все возможные двоичные последовательности, а из них мы уже сами делаем группы и получаем количество различных ожерелий.

В дальнейшем мы ставим задачу изучения математического аппарата, который позволит оптимально считать количество ожерелий и написания программы, которая позволит это сделать для различных n и r.

Итогом исследования является

написанная программа, которая генерирует все двоичные последовательности заданной длины, по которым в дальнейшем можно группировать бусы в классы одинаковых бус.

Исследование опирается на следующие библиографические источники:

1. На материалы занятий дополнительной образовательной программы «Информатика 5» МАОУ ДО ЦДО «Стратегия»
2. сайт http://neerc.ifmo.ru/wiki/index.php?title=Лемма_Бёрнсайда_и_Теорема_Пойа

Данная работа представляет собой одно из решений практически значимой и актуальной задачи по оценке величин физических параметров высокочастотного электромагнитного поля переносных малогабаритных устройств связи (бытовых раций и мобильных телефонов) в различных режимах их работы. Оценка осуществляется с использованием показаний, полученных с помощью разработанного компактного и простого измерительного прибора (датчика), ориентированного на его широкое применение пользователями устройств связи.

Авторы проекта: Блохин Иван, Волков Павел. Ульяновск, лицей при УлГТУ.

FastCast – абсолютно новая социальная сеть, позволяющая Вам и Вашим друзьям мгновенно делиться своими впечатлениями в формате "подкастов".

За пару кликов вы создадите своё уникально оформленное аудиосообщение и мгновенно поделитесь им со своими друзьями.

С помощью интеллектуальной системы подбора подкастов на любую тематику вы всегда будете в курсе интересующих вас трендов.

Fastcast для тех, кому не хватает текста, чтобы выразить свои эмоции. 

Очки для слабовидящих

Авторы: Филатов Роман Александрович

                 Никитин Дмитрий Максимович

МБОУ Экономический лицей №95 г. Новосибирск

Научный руководитель: Глоба А.А., учитель информатики и ИКТ, МБОУ Экономический лицей №95 г. Новосибирск

Постановка целей и задач:

• Разработать программу для очков
• Разработать корпус и устройство очков
• Оптимизировать работу очков в сборе
• Протестировать работу очков

Нами был придуман проект по созданию специальных очков для слабовидящих. С их помощью незрячие люди смогут облегчить свою жизнь. Очки будут работать благодаря компьютерному зрению. Для этого мы будем использовать язык программирования C++, с подключённой библиотекой OpenCV. Данная библиотека позволит нам распознавать препятствия и предметы. Распознавание – главная функция наших очков.

Функционал очков:

Актуальность и значимость

В мире инвалидами по зрению являются 3.5% населения Земли, что равно, примерно, 300 миллионам человек – это актуальная проблема. Мы решили сделать что-то такое, что поможет слабовидящим людям. Поэтому мы разрабатываем очки.

Мир технологий не стоит на месте. Сейчас для незрячих людей уже сделано многое: библиотеки, светофоры, шрифт Брайля и т.д. Но действительно важным изобретением будет являться прибор, который будет содержать в себе функционал, использующий не специально изобретённые устройства для незрячих, а обычные.

Итоги исследования

Нами было придумано устройство, позволяющее незрячим людям комфортно жить в окружающем их мире. На данный момент устройство разрабатывается и совершенствуется.

Список использованной литературы

1. https://habrahabr.ru/company/dataart/blog/303482
2. http://profmed.blogspot.ru/2014/02/blog-post_1230.html
3. http://logic.pdmi.ras.ru/csclub/sites/default/files/CS_Club_2011_February_Vision.pdf

Очки для слабовидящих

Авторы: Филатов Роман Александрович

                 Никитин Дмитрий Максимович

МБОУ Экономический лицей №95 г. Новосибирск

Научный руководитель: Глоба А.А., учитель информатики и ИКТ, МБОУ Экономический лицей №95 г. Новосибирск

Постановка целей и задач:

• Разработать программу для очков
• Разработать корпус и устройство очков
• Оптимизировать работу очков в сборе
• Протестировать работу очков

Нами был придуман проект по созданию специальных очков для слабовидящих. С их помощью незрячие люди смогут облегчить свою жизнь. Очки будут работать благодаря компьютерному зрению. Для этого мы будем использовать язык программирования C++, с подключённой библиотекой OpenCV. Данная библиотека позволит нам распознавать препятствия и предметы. Распознавание – главная функция наших очков.

Функционал очков:

Актуальность и значимость

В мире инвалидами по зрению являются 3.5% населения Земли, что равно, примерно, 300 миллионам человек – это актуальная проблема. Мы решили сделать что-то такое, что поможет слабовидящим людям. Поэтому мы разрабатываем очки.

Мир технологий не стоит на месте. Сейчас для незрячих людей уже сделано многое: библиотеки, светофоры, шрифт Брайля и т.д. Но действительно важным изобретением будет являться прибор, который будет содержать в себе функционал, использующий не специально изобретённые устройства для незрячих, а обычные.

Итоги исследования

Нами было придумано устройство, позволяющее незрячим людям комфортно жить в окружающем их мире. На данный момент устройство разрабатывается и совершенствуется.

Список использованной литературы

1. https://habrahabr.ru/company/dataart/blog/303482
2. http://profmed.blogspot.ru/2014/02/blog-post_1230.html

3.http://logic.pdmi.ras.ru/csclub/sites/default/files/CS_Club_2011_February_Vision.pdf

В работе рассмотрены прямая и обратная задачи теории погрешностей и приведены примеры их применения для решения прикладных задач. В работе показано, что несмотря на некий уровень математической абстракции излагаемого материала, он вполне доступен и имеется возможность построить алгритм применения методов прямой и обратной задач теории погрешностей к решению прикладных задач. Работа сделана по мотивам решения задач на теоретическом и практическом турах регионального этапа (Победитель, 2017 г., Сочи (Краснодар)) Всероссийской олимпиады школьников по физике. Использовался материал Всероссийской олимпиадной школы по физике (Белоруссия, 2016 г.), физической смены в Сириусе (2016 г.) и др.

Работа набрана в LaTex2e

Бочаров Дмитрий Сергеевич

РАЗРАБОТКА И ПРИМЕНЕНИЕ ЧИСЛЕННОГО МЕТОДА, ДЛЯ МОДЕЛИРОВАНИЯ УДАРНИКА ПЕРЕМЕННОГО СЕЧЕНИЯ

МБ НОУ «Гимназия №44» г. Новокузнецк

Научный руководитель: учитель физики Евгений Геннадьевич Тимофеев

Актуальность: разработка численного метода, реализованного посредством алгоритмического языка программирования, является актуальной. Так как данный метод позволяет уйти от использования коммерческого программного обеспечения, что является экономически выгодными при практическом применении.

Цель работы: разработка алгоритмамоделированияцилиндрического ударника переменного сечения с учетом потребностей имеющегося численного метода расчета ударного импульса. Новизна работы: созданный в ходе работы алгоритм формирования ударника из цилиндрических ступеней позволяет использовать имеющийся численный метод расчета ударного импульса без применения элементов интегрального исчисления.

Итоги работы: в ходе выполнения практического исследования был создан алгоритм, позволяющий смоделировать ударник переменного сечения из цилиндрических ступеней конечной длины. Итогом выполнения этого расчета является массив, содержащий численные значения диаметров ступеней, формирующих боек. Данный массив является входным элементом численного метода, рассчитывающего ударный импульс, который формируется при ударе смоделированным ударником по цилиндрическому волноводу полубесконечной длины. Так же показана реализация этого алгоритма на языке программирования ObjectPascal с использованием циклической структуры с предусловием. Практическая значимость: разработанный нами алгоритм был использован при создании расчетной программы «Ударный импульс 2.0», которая прошла государственное освидетельствование и получила номер №2015662766.

Список литературы

1. Открытие №13. Александров. Е.В. Бюл. №7, 1964.
2. Дворников Л.Т. К проблеме описания и оптимизации процесса генерирования волн продольных колебаний в стержневых системах ударных механизмов/ Л.Т. Дворников, А.А. Мясников// тезисы докладов Конференции по распространению упругих и упруго пластических волн. Часть I. – Фрунзе, 15-17 сентября 1983г.
3. Бегагоен И.А. Бурильные машины. Расчет, конструкции, долговечность / И.А. Бегагоен, А.Г. Дядюра, А.И. Бажал. – М.: Недра, 1972. – 368 с.
4. Алимов О.Д. Бурильные машины / О.Д. Алимов, Л.Т. Дворников – М.: Машиностроение, 1976. – 295 с.
5. Манжосов В.К. Модели продольного удара. – Ульяновск: УлГТУ, 2006. – 160 с.
6. Тимофеев Е.Г. Инструментальные средства для автоматизации проектирования машин и механизмов ударного действия/ Е.Г. Тимофеев, И.А. Жуков// тезисы докладов международной Конференции Современные проблемы машиностроения. Часть III. – Улан-Удэ, 2015г.
7. Тимофеев Е.Г. К разработке специализированного программного обеспечения для анализа сложных форм бойков ударных механизмов / Е.Г. Тимофеев, И.А.Жуков // Автоматизированное проектирование в машиностроении. – 2014. – №2.
8. Свидетельство о государственной регистрации программ для ЭВМ №2015662766 от 01.12.2015

Математические знания имеют широкое применение в различных предметных областях. В ландшафтном дизайне математика помогает определить положение объектов для гармоничного восприятия окружающей природы...

    Цель - научиться применять математические методы для решения социальных проблем.

    Задачи:

• Исследовать метод анализ иерархий как способ выбрать одну из набора многих альтернатив при наличии многих критериев.
• Научиться оценивать согласованность данных при голосовании групп людей по нескольким критериям.
• Научиться умножать матрицы.
• Применить полученные знания для выбора старосты класса.
• МАИ - способ выработки решения на основе анализа нескольких критериев.

Актуальность. Тема данного научного исследования посвящена важной проблеме использования математических средств в социальных науках, например, в социологии, психологии, экономике и других. Математические методы можно применять даже в таком важном для школьников вопросе, как выбор старосты класса. Это вопрос актуален для каждого школьника. Так как ответственный староста помогает координировать работу класса и помогает во всевозможных ответственных мероприятиях, являясь во многом эталоном для одноклассников.

Значимость и новизна:

Староста класса должен отвечать ряду требований, чтобы справляться со своими обязанностями по организации совместных школьных мероприятий. Такими качествами должны быть ответственность, активное участие в общественных мероприятиях, высокие результаты в учебе, ну и, конечно, общительность и умение ладить с одноклассниками. А так как претендентов, как правило, несколько, нужно каждого из них проанализировать на наличие и степень выраженности этих важных качеств. И вот здесь нам поможет математика, но математика не простая, которую мы сейчас изучаем в рамках школьной программы, а социальная, то есть применимая к изучению процессов, которые происходят в социальных группах, например, в нашем классе.

Итоги:

• В проведенном эксперименте - выборах староста класса - использованы четыре критерия: умение находить общий язык со всеми, ответственность, дисциплинированность и общительность; в качестве кандидатов выступали четыре ученицы.
• В перспективе планируется пересмотреть набор критериев, по которым производить отбор старосты, провести голосование для классного руководителя и сравнить результаты класса и учителя.

Литература:

1. Саати Т. Принятие решений. Метод анализа иерархий: Пер. с англ. – М.: Радио и связь, 1989. – 316 с.
2. Трахтенгерц Э.А. Компьютерная поддержка принятия решений: Научно-практическое издание. – М.: СИНТЕГ, 1998. – 376 с.
3. Варфоломеев В.И., Воробьев С.Н. Принятие управленческих решений: Учеб пособие для вузов. – М.: КУДИЦ-ОБРАЗ, 2001. – 288 с.

Выполнил: Каплин Артем

[1] имеется ввиду: число идущее следующем не имеет вид (число предшествующее+1)

изучается скорость деградации метоморфных наногетероструктур в зависимости от температуры

ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТРАСОЛОГИЧЕСКИХ МОДЕЛЕЙ В КРИМИНАЛИСТИЧЕСКОЙ ЭКСПЕРТИЗЕ

Королева Ольга

Ученица 7 А класса

МАОУ СОШ 59 «Перспектива», г. Липецк

Сысоев Антон Сергеевич

к.т.н., доцент кафедры прикладной математики ЛГТУ

Хабибуллина Елена Леонидовна

ассистент кафедры прикладной математики ЛГТУ

    Цель - исследовать существующие трасологические модели применительно к подросткам.

    Задачи:

• изучить классические трасологические модели;
• собрать экспериментальные данные среди школьников в возрасте от 12 до 15лет;
• исследовать классические трасологические модели на основе экспериментальных данных;
• построить и проанализировать трасологические модели, построенные по экспериментальным данным.

Актуальность. Но в последнее время, к сожалению, наблюдается рост преступности среди несовершеннолетнего населения. Пропорции частей тела у подростков отличаются от пропорций взрослого человека. Поэтому актуальной является задача исследования трасологических моделей применительно к подросткам.

Итоги:

В результате проделанной работы можно сделать следующие выводы:

– классические трасологические модели плохо подходят для определения роста преступника-подростка;

– построенные регрессионные трасологические модели по экспериментальным данным позволяют гораздо точнее определить рост преступника-подростка;

­– наилучший результат среди построенных моделей показала модель с факторами «длина_следа», «ширина_следа», «длина_шага_правой_ноги», «длина_шага_левой_ноги», «ширина_шага».

Полученные модели помогут определить рост преступник-подростка с допустимым отклонением, но гораздо важнее задача профилактики правонарушений среди несовершеннолетних и поиске эффективных методов борьбы с растущей подростковой преступностью.

Литература:

1. Железняк А.С. Основы криминалистической техники. Учебное пособие. Загл. с экрана. URL: http://www.bnti.ru/showart.asp?aid=979&lvl=01.
2. Размеры тела и их взаимосвязь. Загл. с экрана. URL: http://anfiz.ru/books/item/f00/s00/z0000029/

/st051.shtml

3. "Тревожный показатель": в России уровень детской преступности за год вырос на 5%. Загл. с экрана. URL: https://kprf.ru/activity/children/147084.html
4. Следы ног и обуви. Загл. с экрана. URL: http://www.grandars.ru/college/pravovedenie/sledy-nog.html

ЗАДАЧА О РЮКЗАКЕ И АЛГЕБРА ЛОГИКИ

В ЗАДАЧЕ СОСТАВЛЕНИЯ ШКОЛЬНОГО РАСПИСАНИЯ

Ковалева Екатерина

Ученица 7 А класса

МАОУ СОШ 59 «Перспектива» г. Липецк

Хабибуллина Елена Леонидовна

ассистент кафедры прикладной математики Липецкого государственного технического университета

Меньщикова Татьяна Викторовна

Залуженный учитель РФ, заместитель директора МАОУ СОШ №59 «Перспектива»

    Цель – проверить, ускорит ли процесс составления расписания, соответствующего нормам СанПиН, использование математических методов.

    Задачи:

• изучить требования и пожелания для составления расписаний;
• распределить учебные предметы по дням учебной недели;
• определить порядок учебных предметов в каждый из дней учебной недели;
• провести анализ получившегося расписания.

Актуальность. Одной из важнейших и актуальных задач, решаемых системой управления образовательным учреждением, является составление расписания занятий. При этом формирование расписания учебных занятий для многих школ проблемно, поскольку требует значительных затрат времени и материальных ресурсов.

Значимость:

Удачно составленное расписание в значительной степени определяет:

а) качество обучения;

б) физическое и психологическое здоровье школьников;

в) комфортность учебы школьников и работы преподавательского состава и т. д.

Итоги:

В рамках исследовательской работы были изучены требования к составлению расписания; написана программа «Комбинатор», помогающая распределять предметы по дням недели; при помощи методов алгебры логики были найдены все возможные варианты порядка предметов с учетом пожеланий учителей и требований СанПиН; приведен пример одного из вариантов расписания для 7 «А» класса.

Литература:

1. Информатика. 8 класс: учебник / Л.Л. Босова, А.Ю. Босова. — М.: БИНОМ. Лаборатория знаний.
2. Н.Н. Зепнова, О.В. Кузьмин Применение методов дискретной математики при решении логических задач. Омский научный вестник №2 (130) 2014. С.14-17. [Электронный ресурс]
3. Санитарные правила ст. 28 Федерального закона “О санитарно-эпидемиологическом благополучии населения” программы, методики и режимы воспитания и обучения в части гигиенических требований.

Целью данной работы является знакомство с Египетскими дробями, их исследование и выявление области применения. Я собираюсь выяснить происхождение Египетских дробей, разобраться с основными операциями с ними, научиться решать с их помощью стандартные и нестандартные задачи.

Тезисы к работе.

Метод аутентификации и идентификации пользователей в облачных системах.

Автор: Карташев Павел Юрьевич, 11 класс.

ГБОУ Гимназия №491 "Марьино"

Научный руководитель: отсутствует

Проект посвящен созданию нового алгоритма аутентификации и идентификации пользователя в облачных системах.

В данном проекте исследуются существующие методы и алгоритмы аутентификации и идентификации, из вывода об их недостатках и достоинствах разрабатывается новый метод аутентификации и идентификации, который имеет преимущества как в безопасности, так и в удобстве по сравнению с существующими методами.

Данные проект актуален как никогда в нынешнее время, ведь сейчас так важно позаботиться о защите информации в сети интернет, а также об удобстве её использования пользователями.