
Функция `f(x,y)` называется симметрической, если `f(x,y) = f(y,x)`.
Система уравнений вида , где `f(x,y)`, `g(x,y)` - симметрические, называется симметрической системой. Такие системы решаются чаще всего с помощью введения новых переменных `x+y=u`, `xy=v`.
Решите систему уравнений
Эта алгебраическая (симметрическая) система, обычно она решается заменой `x+y=u`, `xy=v`. Заметив, что
`x^3 +x^3 y^3 +y^3 =(x+y)(x^2 -xy+y^2 )+x^3 y^3 =`
`=(x+y)((x+y)^2 -3xy)+x^3 y^3 =u(u^2 -3v)+v^3`,
перепишем систему в виде
(в старых переменных)
`(2;1), (1;2)`.
Для успешного выполнения задания необходимо помнить, что строго монотонная функция любое своё значение принимает только один раз, т. е. если функция `y(x)` строго монотонна, то для любых `x^** in D(y)`, `x^(** **) in D(y)` следует, что `y(x^**) = y(x^(** **)) iff x^** = x^(** **)`.
Вспомним ещё свойства не просто монотонных функций, а нечётных монотонных.
Если функция нечётная, то при любом `x` из области определения
`f(x) =-f(-x) iff f(x) + f(-x) =0`,
т. е. функция в симметричных точках принимает «противоположные» значения.
В случае произвольной нечётной функции равенство `f(x_1) =-f(x_2)` может выполняться в нескольких точках (не только в симметричных): например,
`sin pi/3 =-sin (- (pi)/3) =- sin (- (2pi)/3)`.
Если же функция нечётная, а к тому же и строго монотонная, то равенство `f(x_1) + f(x_2) =0` выполняется только в симметричных точках - вспомним график функции `y=x^3` - рис. 9.
| Рис. 9 |
Итак, если нечётная и строго монотонная функция, то
`f(x_1) =- f(x_2) iff f(x_1) + f(x_2) =0 iff x_2 =- x_1`.
Поэтому для такой функции `f(x):`
`f(x) + f(g(x)) =0 iff x=- g(x)`.

Основное внимание, как во всех Заданиях, уделяется методам и приёмам решения задач. Именно решение задач делает изучение вообще, и геометрии в частности, активным. Ведь каждая решённая задача - это некоторый поиск и, пусть небольшое, но открытие. «То, что вы были принуждены открыть сами, оставляет в вашем уме дорожку, которой вы сможете воспользоваться, когда в том возникнет необходимость» (это слова немецкого физика XVII столетия Лихтенберга, который известен своими афоризмами).
Итак, если хотите научиться решать задачи, приобрести навыки решения – учитесь этому, разбирайте решения в учебнике и нашем Задании, повторяйте эти решения (ведь так учатся всему), а затем пробуйте свои силы. У Вас получится.
Задание состоит из четырёх параграфов. В параграфе 1 повторяются признаки подобия треугольников, решается несколько характерных задач на эту тему, повторяются свойства медиан, биссектрис и высот треугольника. Во втором параграфе обсуждаются «задачи в делении отрезка» и доказывается теорема Менелая. Третий параграф посвящён свойствам касательных, хорд, секущих, вписанных и описанных четырёхугольников. В параграфе 4 рассматривается применение теорем синусов и косинусов, разобраны задачи, решение которых требует применение тригонометрии. Почти все эти темы разбирались в заданиях по геометрии в 9 и 10 классах ЗФТШ, поэтому более простые утверждения здесь приводятся без доказательства. Тем, кто поступил в ЗФТШ в 11 класс, рекомендуется доказать эти утверждения самостоятельно, а те, кто учится в ЗФТШ не первый год, найдут много новых интересных задач, подробно решённых в 19 примерах.
Задание оканчивается контрольными вопросами и задачами для самостоятельного решения; они оценены по трудности в очках, которые указаны в скобках после номера. Знаком * «звёздочка» отмечены более трудные вопросы и задачи.
За правильный ответ и верное решение задачи ставится полное число очков, за недочёты и ошибки определённое число очков снимается.
Работу над заданием рекомендуется начать с внимательного чтения его и самостоятельного решения (после ознакомления) всех приведённых в нём задач. Ответы на контрольные вопросы следует давать подробные, со ссылками на соответствующие теоремы учебника или данного задания, с доказательствами своих ответов. В случае отрицательного ответа должен быть приведён опровергающий пример. Приведём примеры ответов на контрольные вопросы.
Можно ли утверждать, что треугольник равнобедренный, если его биссектриса является медианой?
Ответ
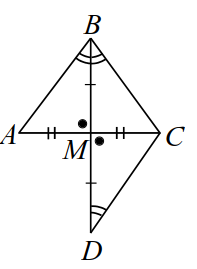 |
| Рис. 1 |
Да, можно. Докажем это. Пусть в треугольнике биссектриса `BM` является медианой: (рис. 1). На продолжении биссектрисы отложим отрезок , равный . Треугольники и равны по первому признаку: у них углы при вершине равны как вертикальные и , . Из равенства треугольников следует
(1)
и . Но , поэтому , т. е. в треугольнике углы при основании равны. По теореме этот треугольник равнобедренный: . Отсюда и из (1) заключаем: . Утверждение доказано.
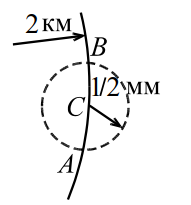 |
| Рис. 2 |
Могут ли длины сторон треугольника быть меньше `1` мм, а радиус описанной окружности больше `1` км?
ОТвет
Да, могут. Приведём пример. Из точки , лежащей на окружности радиуса `2` км, дугой радиуса мм отмечаем точки и , лежащие на большей окружности (рис. 2); очевидно, мм.
Треугольник вписан в окружность радиуса `2` км, а его наибольшая сторона < мм.
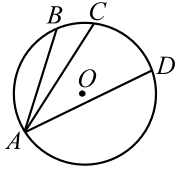 |
| Рис. 3 |
Можно ли через точку окружности провести три равные между собой хорды?
Нет, нельзя. Действительно, предположим противное, т. е. предположим, что хорды , и окружности с центром в точке равны между собой (рис. 3). Тогда точки , и одинаково удалены от точки `A`, т. е. они лежат на окружности с центром в точке . Однако, этого не может быть, так как две окружности с разными центрами не могут иметь более двух общих точек. Значит предположение неверно.
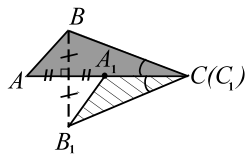 |
| Рис. 4 |
Верно ли, что , если , , ?
Нет, например, на рис. 4 показаны треугольники и , для которых, как легко видеть, выполнены все заданные равенства, но , так как .
Итак, при утвердительном ответе надо либо привести доказательство того, что данное утверждение верно (как в ответе на вопрос 1), либо привести конкретный пример реализации заданных условий (как в ответе на вопрос 2).
При отрицательном ответе надо либо привести рассуждения, приводящие к противоречию заданных условий аксиоме, теореме или определению (как в ответе на вопрос 3), либо построить один опровергающий пример (как в ответе на вопрос 4).
После повторения тем в §1 – 4 в заключительном пятом параграфе обсудим вопросы подходов к решению, важность хорошего рисунка, выбора переменных, а также остановимся на некоторых ошибках, допускаемых учащимися и абитуриентами.
Это задание вместе с присланным решением будут Вам полезны при подготовке к экзаменам.

Две фигуры $$ F$$ и $$ {F}^{\text{'}}$$ называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры $$ F$$ и $$ {F}^{\text{'}}$$ подобны, то пишется $$ F\sim {F}^{\text{'}}$$Напомним, что в записи подобия треугольников $$ ∆ABC~∆{A}_{1}{B}_{1}{C}_{1}$$ предполагается, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. $$ A$$ переходит в $$ {A}_{1}$$, $$ B$$ - в $$ {B}_{1}$$, $$ C$$ - в $$ {C}_{1}$$. Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если $$ ∆ABC~∆{A}_{1}{B}_{1}{C}_{1}$$
$$ \angle A=\angle {A}_{1}, \angle B=\angle {B}_{1}, \angle C=\angle {C}_{1}, {\displaystyle \frac{AB}{{A}_{1}{B}_{1}}}={\displaystyle \frac{BC}{{B}_{1}{C}_{1}}}={\displaystyle \frac{AC}{{A}_{1}{C}_{1}}}$$.
Два треугольника подобны:
Из признаков подобия следует утверждения, которые удобно использовать в решении задач:
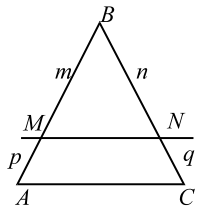
1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.
 |
| Рис. 5 |
2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если $$ MN\left|\right|AC$$ (рис. 5), то
$$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{p}{q}}=\frac{m+p}{n+q}$$
3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)
$$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{m+p}{n+q}}$$ или $$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{p}{q}}$$,
то $$ MN$$ параллельна $$ AC$$ (доказательство было дано в задании для 9 класса).
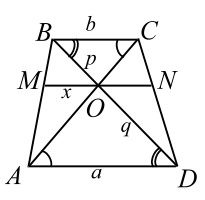
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках $$ M$$ и $$ N$$. Найти длину отрезка `MN`, если основания трапеции равны $$ a$$ и $$ b$$.
Пусть $$ O$$ точка пересечения диагоналей трапеции (рис. 6). Обозначим:
$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$
$$1.\;\left.\begin{array}{l}BC\parallel AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(\mathrm{по}\;\mathrm{двум}\;\mathrm{углам})\end{array}\right|\Rightarrow\dfrac ba=\dfrac pq$$ (1)
$$2.\;\left.\begin{array}{l}MO\parallel AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end{array}\right|\Rightarrow\dfrac xa=\dfrac p{p+q}$$. (2)
Из (1) и (2) следует $$ x=a{\displaystyle \frac{p}{p+q}}=q{\displaystyle \frac{p/q}{p/q+1}}={\displaystyle \frac{ab}{a+b}}$$, т. е. $$ MO={\displaystyle \frac{ab}{a+b}}.$$
Аналогично устанавливаем, что $$ NO={\displaystyle \frac{ab}{a+b}}$$, поэтому $$ \overline{)MN={\displaystyle \frac{2ab}{a+b}}}$$.
Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.
 |
| Рис. 6 |
Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.
 |
| Рис. 7 |
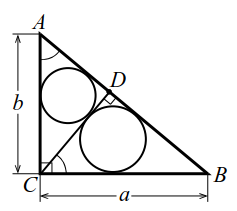
В прямоугольном треугольнике $$ ABC$$ из вершины $$ C$$ прямого угла проведена высота $$ CD$$ (рис. 7). Радиусы окружностей, вписанных в треугольники $$ ACD$$ и $$ BCD$$ равны соответственно $$ {r}_{1}$$ и $$ {r}_{2}$$. Найти радиус окружности, вписанной в треугольник $$ ABC$$.
Обозначим искомый радиус $$ r$$, положим $$ AB=c$$, $$ AC=b$$, $$ BC=a$$. Из подобия прямоугольных треугольников $$ ACD$$ и $$ ABC$$ (у них равные углы при вершине $$ A$$) имеем $$ {\displaystyle \frac{r}{{r}_{1}}}={\displaystyle \frac{c}{b}}$$, откуда $$ b={\displaystyle \frac{{r}_{1}}{r}}c$$. Прямоугольные треугольники $$ BCD$$ и $$ BAC$$ также подобны, поэтому $$ {\displaystyle \frac{r}{{r}_{2}}}={\displaystyle \frac{c}{a}}$$, - откуда $$ a={\displaystyle \frac{{r}_{2}}{r}}c$$. Так как $$ {a}^{2}+{b}^{2}={c}^{2}$$ то, возводя в квадрат выражения для $$ a$$ и $$ b$$ и складывая их, получим $$ {\left(\frac{{r}_{1}}{r}\right)}^{2}{c}^{2}+{\left(\frac{{r}_{2}}{r}\right)}^{2}{c}^{2}={c}^{2}$$ или $$ {\displaystyle \frac{{r}_{1}^{2}+{r}_{2}^{2}}{{r}^{2}}}=1$$. Находим $$ r=\sqrt{{{r}_{1}}^{2}+{{r}_{2}}^{2}}$$.
Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.
 |
| Рис. 8 |
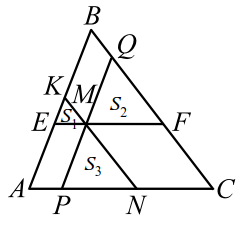
Через точку $$ M$$, лежащую внутри треугольника $$ ABC$$, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны $$ {S}_{1}$$, $$ {S}_{2}$$ и $$ {S}_{3}$$. Найти площадь треугольника $$ ABC$$.
Легко видеть, что треугольники $$ EKM$$, $$ MQF$$ и $$ PMN$$ подобны треугольнику $$ ABC$$.
Пусть $$ S$$ -площадь треугольника $$ ABC$$, тогда
$$ {\displaystyle \frac{{S}_{1}}{S}}={\left({\displaystyle \frac{EM}{AC}}\right)}^{2}; {\displaystyle \frac{{S}_{2}}{S}}={\left({\displaystyle \frac{MF}{AC}}\right)}^{2}; {\displaystyle \frac{{S}_{3}}{S}}={\left({\displaystyle \frac{PN}{AC}}\right)}^{2}.$$
Откуда находим
$$ EM=\sqrt{{\displaystyle \frac{{S}_{1}}{S}}}AC, MF=\sqrt{{\displaystyle \frac{{S}_{2}}{S}}}AC, PN=\sqrt{{\displaystyle \frac{{S}_{3}}{S}}}AC.$$
А так как $$ EM=AP, MF=NC$$, то $$ EM+PN+MF=AP+PN+NC=AC$$.
Таким образом, $$ AC=AC·\left(\sqrt{{\displaystyle \frac{{S}_{1}}{S}}}+\sqrt{{\displaystyle \frac{{S}_{2}}{S}}}+\sqrt{{\displaystyle \frac{{S}_{3}}{S}}}\right)$$, откуда следует
$$ S={\left(\sqrt{{S}_{1}}+\sqrt{{S}_{2}}+\sqrt{{S}_{3}}\right)}^{2}$$.
Свойства медиан, высот, биссектрис треугольника
В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.
 |
| Рис. 9 |
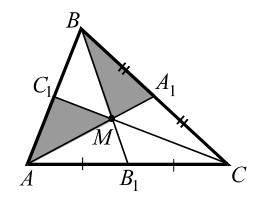
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.
Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.
(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна $$ {\displaystyle \frac{1}{2}}{S}_{ABC}$$. Точка пересечения медиан называется центром тяжести треугольника.
Теорема 3. Пусть $$ BD$$ - медиана треугольника
$$ ABC (BC=a, AC=b, AB=c, BD={m}_{a})$$, тогда
$$ {m}_{c}^{2}={\displaystyle \frac{{a}^{2}+{b}^{2}}{2}}-{\displaystyle \frac{{c}^{2}}{4}}$$. (Доказательство приведено далее в §4 Задания).
 |
| Рис. 10 |
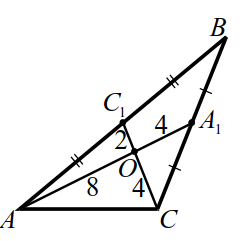
Медианы $$ A{A}_{1}$$ треугольника $$ ABC$$ пересекаются в точке $$ O$$, $$ A{A}_{1}=12$$ и $$ C{C}_{1}=6$$ и одна из сторон треугольника равна `12`. (рис. 10). Найти площадь треугольника $$ ABC$$.
1. По теореме 1 имеем $$ AO={\displaystyle \frac{2}{3}}A{A}_{1}=8$$, $$ CO={\displaystyle \frac{2}{3}}C{C}_{1}=4$$.
Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона $$ AC$$ не может равняться `12`, иначе $$ AC=AO+OC$$ - нарушено неравенство треугольника. Также не может равняться `12` сторона $$ AB$$, так в этом случае $$ A{C}_{1}=6$$ и треугольник $$ AO{C}_{1}$$ со сторонами `8`, `2`, `6` не существует. Значит, $$ BC=12$$ и $$ A{C}_{1}=6$$.
2. Площадь треугольника находим по формуле Герона:
$$ p=7, {S}_{{A}_{1}OC}=\sqrt{7·1·3·3}=3\sqrt{7}$$.
По теореме 2 площадь треугольника $$ ABC$$ в `6` раз больше, находим $$ {S}_{ABC}=18\sqrt{7}$$.
Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.
Были доказаны также две леммы о высотах
1-ая лемма.
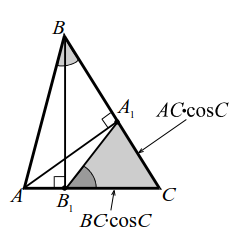
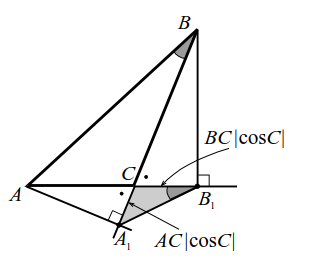
Если $$ A{A}_{1}$$ и $$ B{B}_{1}$$ - высоты треугольника $$ ABC$$, то треугольник $$ {A}_{1}{B}_{1}C$$ подобен треугольнику $$ ABC$$ с коэффициентом подобия $$ k={\displaystyle \frac{{A}_{1}{B}_{1}}{AB}}=\left|\mathrm{cos}C\right|$$. Можно это утверждение сформулировать так: Если соединить основания двух высот $$ A{A}_{1}$$ и $$ B{B}_{1}$$ треугольника $$ ABC$$, то образуется треугольник, подобный данному: $$ ∆{A}_{1}{B}_{1}C~∆ABC$$.
Из прямоугольных треугольников $$ AC{A}_{1}$$ следует $$ {A}_{1}C=AC·\mathrm{cos}C$$ или $$ {A}_{1}C=AC·\mathrm{cos}(180°-C)=AC\left|\mathrm{cos}C\right|$$ (рис. 11а, б), а из прямоугольных треугольников $$ BC{B}_{1}$$ следует $$ {B}_{1}C=BC·\mathrm{cos}C$$ или $$ {B}_{1}C=BC·\mathrm{cos}(180°-C)=BC\left|\mathrm{cos}C\right|$$. Далее рассуждения очевидны.
 |
 |
| Рис. 11a | Рис. 11б |
2-ая лемма.
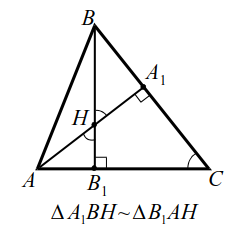
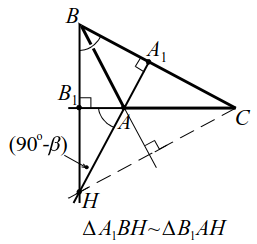
Если высоты $$ A{A}_{1}$$ и $$ B{B}_{1}$$ (или их продолжения) пересекаются в точке $$ H$$, то справедливо равенство $$ AH·H{A}_{1}=BH·H{B}_{1}$$ (рис. 12а, б).
 |
 |
| Рис. 12a | Рис. 12б |
 |
| Рис. 13 |
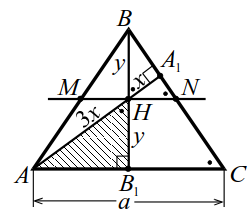
Высоты $$ A{A}_{1}$$ и $$ B{B}_{1}$$ пересекаются в точке $$ H$$ (рис. 13), при этом $$ AH=3H{A}_{1}$$ и $$ BH=H{B}_{1}$$. Найти косинус угла $$ ACB$$ и площадь треугольника $$ ABC$$, если $$ AC=a$$.
Обозначим $$ H{A}_{1}=x, H{B}_{1}=y$$,
1. Точка $$ H$$ - середина высоты (рис. 13). Если отрезок $$ MH$$ проходит через точку $$ H$$ и параллелен основаниям, то `MN` - средняя линия; `MN=a/2`.
2. $$\left.\triangle HA_1N\sim\triangle AA_1C\right|\Rightarrow\dfrac{HN}{AC}=\dfrac x{4x},\;HN=\dfrac14a.$$ Значит, $$ MH=HN={\displaystyle \frac{a}{4}}$$ и $$ A{B}_{1}={B}_{1}C={\displaystyle \frac{a}{2}}$$ Треугольник $$ ABC$$ равнобедренный, $$ AB=BC$$.
3. $$ \angle {B}_{1}BC=90°-\angle C$$, поэтому `ul(/_BHA_1=/_AHB_1=/_C)`, а по второй лемме о высотах $$ AH·H{A}_{1}=BH·H{B}_{1}$$ т. е. $$ 3{x}^{2}={y}^{2}, y=x\sqrt{3}$$.
Далее, $$ \mathrm{cos}C=\mathrm{cos}(\angle AH{B}_{1})={\displaystyle \frac{y}{3x}}$$, находим $$ \mathrm{cos}C={\displaystyle \frac{1}{\sqrt{3}}}$$.
4. $$ △AH{B}_{1}: A{B}_{1}^{2}=(3x{)}^{2}-{y}^{2}$$, $$ {\displaystyle \frac{{a}^{2}}{4}}=6{x}^{2}$$, $$ x={\displaystyle \frac{a}{2\sqrt{6}}}$$, $$ y={\displaystyle \frac{a}{2\sqrt{2}}}$$, тогда
$$ {S}_{ABC}={\displaystyle \frac{1}{2}}AC·B{B}_{1}=ay={\displaystyle \frac{{a}^{2}\sqrt{2}}{4}}$$.
Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если $$ AD$$ - биссектриса треугольника $$ ABC$$ (рис. 14), то
$$ {\displaystyle \frac{BD}{DC}}={\displaystyle \frac{AB}{AC}} \left({\displaystyle \frac{x}{y}}={\displaystyle \frac{c}{b}}\right)$$
Доказательство легко выполните сами, применяя теорему синусов к треугольникам $$ ADB$$ и $$ ADC$$.
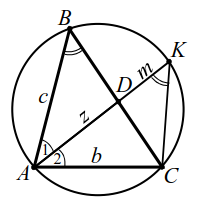
Теорема 6. Пусть $$ AD$$ - биссектриса треугольника $$ ABC$$ (рис. 14), тогда $$ AD=\sqrt{AB·AC-DB·DC}$$ (в обозначениях рисунка 14а)
`ul(AD=sqrt(bc-xy))`.
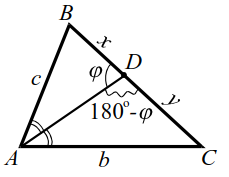 |
 |
||
| Рис. 14 | Рис. 14а |
Эту теорему докажем. Опишем около треугольника $$ ABC$$ окружность, точку пересечения прямой $$ AD$$ и окружности обозначим $$ K$$ (рис. 14а).
Обозначим $$ AD=z, DK=m.△ABD\sim ∆AKC$$ $$ (\angle ABD=\angle AKC$$ и $$ \angle 1=\angle 2)$$. Из подобия следует $$ {\displaystyle \frac{AB}{AK}}={\displaystyle \frac{AD}{AC}}$$, т. е. $$ {\displaystyle \frac{c}{z+m}}={\displaystyle \frac{z}{b}}$$, откуда $$ {z}^{2}+zm=bc$$, $$ {z}^{2}=bc-zm$$.
По свойству пересекающихся хорд: $$ AD·DK=BD·CD$$, т. е. $$ z·m=x·y$$, тогда $$ {z}^{2}=bc-xy$$, $$ z=\sqrt{bc-xy}$$.
В треугольнике $$ ABC$$ со сторонами $$ AB=5$$, $$ AC=3$$ биссектриса $$ AD={\displaystyle \frac{15}{8}}$$. Найти сторону $$ BC$$ и радиус вписанной окружности.
По теореме 5 (см. рис. 14) имеем $$ {\displaystyle \frac{x}{y}}={\displaystyle \frac{5}{3}}$$ Обозначим $$ x=5z$$, тогда $$ y=3z$$. По теореме 6 выполнено равенство $$ {\left({\displaystyle \frac{15}{8}}\right)}^{2}=5·3-5z·3z.$$ Легко находим $$ z={\displaystyle \frac{7}{8}}$$ значит `ul(BC=7)`. Радиус вписанной окружности найдём по формуле $$ S=pr$$ (`S` - площадь треугольника, `p` -полупериметр). Имеем $$ p={\displaystyle \frac{15}{2}}$$, по формуле Герона $$ S=\sqrt{{\displaystyle \frac{15}{2}}·{\displaystyle \frac{1}{2}}·{\displaystyle \frac{10}{2}}·{\displaystyle \frac{9}{2}}}={\displaystyle \frac{15\sqrt{3}}{2}},$$ поэтому $$ r={\displaystyle \frac{S}{p}}={\displaystyle \frac{\sqrt{3}}{2}}.$$

Задача о «делении отрезка», как правило, решаются дополнительным построением – проведением прямой, параллельной рассекающей, и использованием подобия или теоремы о пересечении сторон угла параллельными прямыми. Общий подход к решению таких задач даёт теорема Менелая (далее напомним формулировку и доказательство, в задании 9-го класса это уже было сделано).
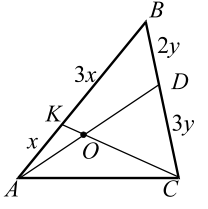
Точка $$ D$$ лежит на стороне $$ BC$$, точка $$ K$$ - на стороне $$ AB$$ треугольника $$ ABC$$, прямые $$ AD$$ и $$ CK$$ пересекаются в точке $$ O$$ (рис. 15). Найти отношение $$ AO:OD$$, если $$ AK:KB=1:3$$ и $$ BD:DC=2:3$$.
 |
| Рис. 15 |
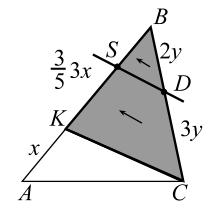
Расставим на рисунке данные о делении сторон. Чтобы решение стало более понятным, сделаем ещё один рисунок (рис. 15а), на нём проведём $$ DS\left|\right|CK$$.
Рассматриваем треугольник $$ KBC$$. Из `DS``||``CK`
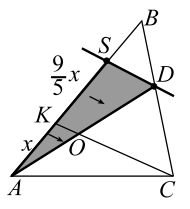
(второй признак подобия треугольников) следует $$ KS:KB=CD:CB$$, откуда $$ KS={\displaystyle \frac{3}{5}}·3x={\displaystyle \frac{9}{5}}x$$. (Ставим это на рисунке). На этом этапе удобно сделать ещё один рисунок (рис. 15б), либо на рисунке 15а провести прямую `AD` и отметить точку $$ O$$.
В треугольнике $$ ASD$$ по построению $$ SD\left|\right|KO$$, По утверждению $$ 2°$$ имеем $$ AO:OD=AK:KS$$, откуда следует $$ AO:OD=5:9$$
 |
 |
| Рис. 15a | Рис. 15б |
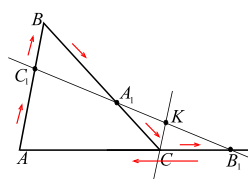
Точки `A_1` и `C_1`, расположенные на сторонах `BC` и `AB` треугольника `ABC`, и точка `B_1`, расположенная на продолжении стороны `AC` за точку `C`, лежат на одной прямой тогда и только тогда, когда имеет место равенство:
$$ {\displaystyle \frac{A{C}_{1}}{{C}_{1}B}}·{\displaystyle \frac{B{A}_{1}}{{A}_{1}C}}·{\displaystyle \frac{C{B}_{1}}{{B}_{1}A}}=1$$. (`**`)
Проводим $$ CK\left|\right|AB$$ (рис. 16а):
$$\begin{array}{l}\left.\triangle A_1CK\sim\triangle A_1BC_1\right|\Rightarrow\dfrac{CK}{C_1B}=\dfrac{A_1C}{BA_1};\\\left.\triangle B_1AC_1\sim\triangle B_1CK\right|\Rightarrow\dfrac{AC_1}{CK}=\dfrac{B_1A}{B_1C}.\end{array}$$
Почленно перемножив, получим
$$ {\displaystyle \frac{A{C}_{1}}{{C}_{1}B}}={\displaystyle \frac{{A}_{1}C}{B{A}_{1}}}·{\displaystyle \frac{{B}_{1}A}{C{B}_{1}}}$$,
откуда и следует
$$ {\displaystyle \frac{A{C}_{1}}{{C}_{1}B}}·{\displaystyle \frac{B{A}_{1}}{{A}_{1}C}}·{\displaystyle \frac{C{B}_{1}}{{B}_{1}A}}=1$$
(стрелочки на рис. 16а показывают последовательность взятия отрезков, движение начинается в точке `A` и в ней же заканчивается).
 |
 |
| Рис. 16а | Рис. 16б |
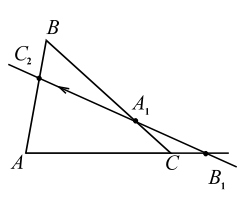
2. Пусть имеет место равенство (`**`). Через две точки $$ {B}_{1}$$ и $$ {A}_{1}$$ проводим прямую, точку пересечения с отрезком $$ AB$$ обозначаем $$ {C}_{2}$$ (рис. 16б). Точки $$ {A}_{1},{B}_{1}$$ и $$ {C}_{2}$$ лежат на одной прямой, по доказанному имеет место
$$ {\displaystyle \frac{A{C}_{1}}{{C}_{1}B}}·{\displaystyle \frac{B{A}_{1}}{{A}_{1}C}}·{\displaystyle \frac{C{B}_{1}}{{B}_{1}A}}=1.$$
Сравнивая с равенством (`**`), устанавливаем, что $$ {\displaystyle \frac{A{C}_{2}}{{C}_{2}B}}={\displaystyle \frac{A{C}_{1}}{{C}_{1}B}}$$ и показываем, что точки $$ {C}_{2}$$ и $$ {C}_{1}$$ совпадают, т. к. делят отрезок $$ AB$$ на равные отрезки.
Применим теорему Менелая к решению примера 7 (см. рис. 15): рассматриваем треугольник $$ BAD$$ и секущую $$ CK$$ (она определяет три точки: $$ K,O,C$$ ). Имеем: $$ {\displaystyle \frac{BK}{KA}}·{\displaystyle \frac{AO}{OD}}·{\displaystyle \frac{DC}{CB}}=1$$,
т. е. $$ {\displaystyle \frac{3x}{x}}·{\displaystyle \frac{AO}{OD}}·{\displaystyle \frac{3y}{5y}}=1$$ откуда $$ {\displaystyle \frac{AO}{OD}}={\displaystyle \frac{5}{9}}$$.
Если при тех же условиях задачи 7 требуется определить, какую часть площади треугольника составляет, например, площадь четырёхугольника $$ KODB$$ то полезно сначала решить задачу о «делении отрезка» и найти, например, $$ AO:OD=5:9$$, а затем использовать тот факт, что площади треугольников с одинаковыми высотами относятся как длины их оснований:
$$ {S}_{ABC}=S; {S}_{ADC}={\displaystyle \frac{3}{5}}S$$ $$ ($$ т. к. $$ DC={\displaystyle \frac{3}{5}}BC$$$$ )$$;
$$ {S}_{OCD}={\displaystyle \frac{9}{14}}{S}_{ADC}={\displaystyle \frac{9}{14}}\left({\displaystyle \frac{3}{5}}S\right)={\displaystyle \frac{27}{70}}S$$ $$ ($$ т. к. $$ OD={\displaystyle \frac{9}{14}}AD$$$$ )$$;
$$ {S}_{KCB}={\displaystyle \frac{3}{4}}S$$ $$ ($$ т. к. $$ BK={\displaystyle \frac{3}{4}}AB$$$$ )$$, поэтому
$$ {S}_{KODB}={S}_{KCB}-{S}_{OCD}={\displaystyle \frac{3}{4}}S-{\displaystyle \frac{27}{70}}S={\displaystyle \frac{51}{140}}S$$.

 |
| Рис. 17 |
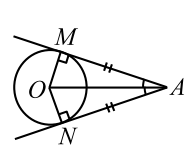
Если из точки к окружности проведены две касательные, то длины отрезков от этой точки до точек касания равны и прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам (рис. 17).
Используя это свойство, легко решить следующую задачу.
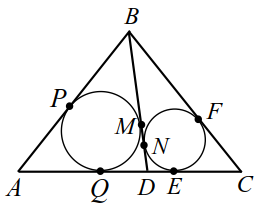
На основании $$ AC$$ равнобедренного треугольника $$ ABC$$ расположена точка $$ D$$ так, что $$ AD=a,CD=b$$. Окружности, вписанные в треугольники $$ ABD$$ и $$ DBC$$, касаются прямой $$ BD$$ в точках $$ M$$ и $$ N$$ соответственно. Найти отрезок $$ MN$$.
 |
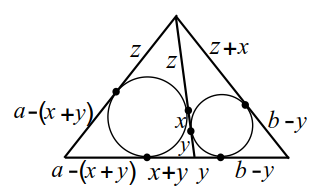 |
| Рис. 18 | Рис. 18a |
Пусть $$ a>b.$$ Точки касания окружностей со сторонами треугольника $$ ABC$$ обозначим и $$ F$$ (рис. 18). Положим По свойству касательных:
$$ DE=y$$, $$ QD=x+y$$, $$ AQ=AP=a-(x+y)$$, $$ EC=CF=b-y$$, $$ PB=BM=z, BF=BN=z+x$$ (рис. 18а). Выразим боковые стороны:
$$ AB=z+a-x-y$$, $$ BC=z+x+b-y$$. По условию $$ AB=BC$$; получим
$$ z+a-x-y=z+x+b-y$$, откуда находим $$ x={\displaystyle \frac{a-b}{2}}$$.
Если $$ a
Итак: $$ MN={\displaystyle \frac{\left|a-b\right|}{2}}.$$
Четырёхугольник называется описанным около окружности, если окружность касается всех его сторон.
В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин противолежащих сторон равны.
 |
| Рис. 19 |
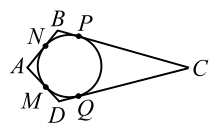
Пусть четырёхугольник $$ ABCD$$ описан около окружности (рис. 19).
По свойству касательных: $$ AM=AN$$, $$ NB=BP$$, $$ PC=CQ$$ и $$ QD=DM$$, поэтому
$$ AM+MD+BP+PC=AN+NB+CQ+QD$$, что означает
$$ AD+BC=AB+CD$$.
Докажем обратное утверждение. Пусть в выпуклом четырёхугольнике $$ ABCD$$ стороны удовлетворяют условию $$ AB+CD=BC+AD.$$ Положим $$ AD=a, AB=b, BC=c, CD=d.$$
По условию $$ a+c=b+d,$$ что равносильно $$ c-b=d-a.$$
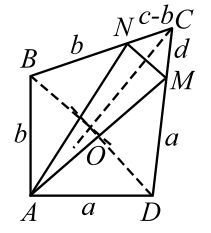
Пусть $$ d>a.$$ Отложим на большей стороне $$ CD$$ меньшую сторону `DM=a` (рис. 20). Так как в этом случае $$ c>b$$, то также отложим $$ BN=b$$, получим три равнобедренных треугольника `ABN`, `ADM` и `MCN`.
 |
| Рис. 20 |
В равнобедренном треугольнике биссектриса угла при вершине является медианой и высотой, отсюда следует, что если провести биссектрисы углов `B`, `C` и `D`, то они разделят пополам соответственно отрезки `AN`, `MN` и `AM` и будут им перпендикулярны. Это означает, что биссектрисы будут серединными перпендикулярами трёх сторон треугольника $$ ANM$$, а они по теореме пересекаются в одной точке. Обозначим эту точку $$ O$$. Эта точка одинаково удалена от отрезков `AB` и `BC` (лежит на $$ OB$$), `BC` и `CD` (лежит на $$ OC$$) и `CD` и `AD` (лежит на $$ OD$$), следовательно, точка $$ O$$ одинакова удалена от всех четырёх сторон четырёхугольника $$ ABCD$$ и является центром вписанной окружности. Случай $$ d=a$$, как более простой, рассмотрите самостоятельно.
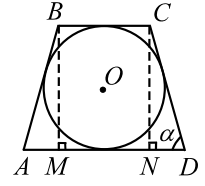
Равнобокая трапеция описана около окружности. Найти радиус окружности, если длины оснований равны $$ a$$ и $$ b$$.
 |
| Рис. 21 |
Пусть в равнобокой трапеции $$ ABCD$$ `BC=b`, `AD=a` (рис. 21). Эта трапеция равнобокая $$ (AB=CD)$$, она описана около окружности, следовательно, $$ AB+CD=AD+BC$$ Отсюда получаем:
$$ AB=CD={\displaystyle \frac{a+b}{2}}.$$
Проведём $$ BM$$ и $$ CN$$ перпендикулярно $$ AD$$. Трапеция равнобокая, углы при основании равны, следовательно, равны и треугольники $$ ABM$$ и $$ DCN$$ и $$ AM=ND$$. По построению $$ MBCN$$ - прямоугольник, $$ MN=BC=b$$ поэтому $$ AM={\displaystyle \frac{1}{2}}(AD-BC)-{\displaystyle \frac{1}{2}}(a-b)$$. Из прямоугольного треугольника $$ ABM$$ находим высоту трапеции $$ ABCD$$:
$$ BM=\sqrt{A{B}^{2}-A{M}^{2}}=\sqrt{{\left({\displaystyle \frac{a+b}{2}}\right)}^{2}-{\left({\displaystyle \frac{a-b}{2}}\right)}^{2}}=\sqrt{ab}$$.
Очевидно, что высота трапеции равна диаметру окружности, поэтому
радиус вписанной окружности равен $$ \overline{)r={\displaystyle \frac{1}{2}}\sqrt{ab}}$$.
Очень полезная задача. Заметим, что из решения также следует, что в равнобокой описанной трапеции $$ \overline{)\mathrm{cos}\alpha ={\displaystyle \frac{a-b}{a+b}}}$$.
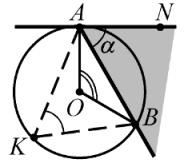
Градусная мера угла, образованного хордой и касательной, имеющими общую точку на окружности, равна половине градусной меры дуги, заключённой между его сторонами (рис. 22).
 |
| Рис. 22 |
Рассматриваем угол $$ NAB$$ между касательной $$ NA$$ и хордой $$ AB$$. Если $$ O$$ - центр окружности, то $$ OA\perp AN$$, `/_OAB=/_OBA=90^@alpha`. Сумма углов треугольника равна `180^@`, следовательно, $$ \angle AOB=2\alpha $$. Итак, $$ \alpha =\angle NAB={\displaystyle \frac{1}{2}}\angle AOB.$$
Обратим внимание, что угол $$ NAB$$ равен любому вписанному углу $$ AKB$$, опирающемуся на ту же дугу $$ AB$$.
Случай `/_alpha>=90^@` рассматривается аналогично.
Из этого свойства следует важная теорема «о касательной и секущей», которая часто используется при решении задач.
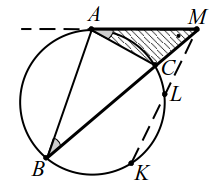
Пусть к окружности проведены из одной точки касательная $$ MA$$ и секущая $$ MB$$, пересекающая окружность в точке $$ C$$ (рис. 23). Тогда справедливо равенство
$$ M{A}^{2}=MB·MC$$
т. е. если из точки `M` к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки `M` до точки касания равен произведению длин отрезков секущей от точки `M` до точек её пересечения с окружностью.
Угол $$ MAC$$ образован хордой и касательной, $$ \angle MAC=\angle ABC$$. Так как в треугольниках $$ MAC$$ и $$ MBA$$ угол $$ M$$ общий, то по двум углам они подобны. Из подобия следует:
$$ {\displaystyle \frac{MA}{MB}}={\displaystyle \frac{MC}{MA}}$$
Откуда получаем: $$ M{A}^{2}=MB·MC$$.
 |
| Рис. 23 |
Если из точки $$ M$$ к окружности проведены две секущие: $$ MB$$, пересекающая окружность в точке $$ C$$ и $$ MK$$, пересекающая окружность в точке $$ L$$ (рис. 23), то справедливо равенство $$ MB·MC=MK·ML$$.
Проведём касательную $$ MA$$. По доказанной теореме $$ M{A}^{2}=MB·MC$$ и $$ M{A}^{2}=MK·ML$$, следовательно $$ MB·MC=MK·ML$$.
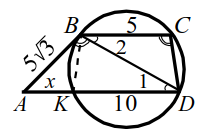 |
| Рис. 24 |
Окружность проходит через вершины $$ C u D$$ трапеции $$ ABCD,$$ касается боковой стороны $$ AB$$ в точке $$ B$$ и пересекает большее основание $$ AD$$ в точке $$ K$$ (рис. 24). Известно, что $$ AB=5\sqrt{3}$$, $$ BC=5$$ и $$ KD=10$$.
Найти радиус окружности.
1. Пусть $$ AK=x$$ тогда $$ AD=10+x$$ю
По теореме о касательной и секущей:
$$ A{B}^{2}=AK·KD$$ т. е. $$ 75=x(x+10)$$, откуда $$ x=5$$. Итак $$ AD=15$$.
2. Заметим теперь, что угол $$ ABD$$ между касательной $$ AB$$ и хордой $$ BD$$ равен вписанному углу $$ BCD$$, а из параллельности прямых $$ AD$$ и $$ BC$$ следует равенство углов `1` и `2`. По первому признаку подобия $$ △ABD\sim △DCB$$. Из подобия имеем $$ {\displaystyle \frac{AB}{CD}}={\displaystyle \frac{AD}{BD}}{\displaystyle \frac{BD}{BC}}$$. Из последнего равенства находим, что $$ B{D}^{2}=AD·BC$$, т. е. $$ BD=\sqrt{AD·BC}=5\sqrt{3}$$, а из первого равенства находим $$ CD={\displaystyle \frac{AB·BD}{AB}}=5$$.
3. Так как $$ KB=CD$$ ($$ KBCD$$ - вписанная трапеция, она равнобокая), и $$ K{B}^{2}+B{D}^{2}=K{D}^{2},$$ то `/_ KBD=90^@` и $$ KD$$ - диаметр окружности.
Значит, её радиус равен `5`.
Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противолежащих углов равна `180^@`.
Из этой теоремы следует:
a) из всех параллелограммов только около прямоугольника можно описать окружность;
б) около трапеции можно описать окружность только тогда, когда она равнобокая.
 |
| Рис. 25 |
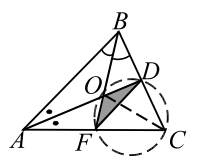
В треугольнике $$ ABC$$ биссектрисы $$ AD$$ и $$ BF$$ пересекаются в точке $$ O$$ (рис. 25). Известно, что точки $$ F, O, D$$, и `C` лежат на одной окружности и что $$ DF=\sqrt{3}.$$ Найти площадь треугольника $$ ODF$$.
Так как
$$ \angle BAO={\displaystyle \frac{1}{2}}\angle A$$ и $$ \angle ABO={\displaystyle \frac{1}{2}}\angle B$$, то
$$ \angle DOF=\angle AOB=\pi -{\displaystyle \frac{1}{2}}(\angle A+\angle B)$$.
Четырёхугольник $$ DOFC$$ вписан в окружность, по теореме 9:
$$ \angle DOF=\pi -\angle C$$, т. е. $$ \pi -{\displaystyle \frac{1}{2}}(\angle A+\angle B)=\pi -\angle C$$, откуда, учитывая, что $$ \angle A+\angle B+\angle C=\pi $$, находим $$ \angle С={\displaystyle \frac{\pi }{3}}$$.
Теперь заметим, что $$ O$$ - точка точка пересечения биссектрис, $$ CO$$ - биссектриса угла $$ C,$$ следовательно, углы $$ OCD$$ и $$ OCF$$ равны друг другу. Это вписанные углы, поэтому вписанные углы $$ ODF$$ и $$ OFD$$ равны им и равны друг другу. Таким образом,
$$ \angle ODF=\angle OFD={\displaystyle \frac{1}{2}}\angle C={\displaystyle \frac{\pi }{6}}$$.
Треугольник $$ DOF$$ равнобедренный с основанием $$ DF=\sqrt{3}$$ и углом при основании `30^@`. Находим его высоту, опущенную из вершины $$ O$$ и площадь треугольника $$ ODF: S={\displaystyle \frac{1}{2}}h·DF={\displaystyle \frac{\sqrt{3}}{4}}$$.

Как обычно, в треугольнике $$ ABC$$ стороны, противолежащие углам `A`, `B` и `C`, обозначим `a`, `b` и `c`. Справедливы две теоремы, устанавливающие соотношения между сторонами и углами треугольника, утверждения которых можно кратко записать так:
теорема косинусов: $$ {c}^{2}={a}^{2}+{b}^{2}-2ab\mathrm{cos}C;$$
теорема синусов: $$ {\displaystyle \frac{a}{\mathrm{sin}A}}={\displaystyle \frac{b}{\mathrm{sin}{\displaystyle B}}}={\displaystyle \frac{c}{\mathrm{sin}{\displaystyle C}}}=2R$$.
Покажем на примерах, как применяются эти теоремы.
 |
| Рис. 26 |
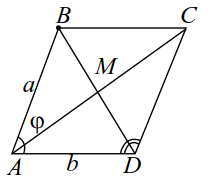
Доказать, что в параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его сторон.
Пусть в параллелограмме $$ ABCD$$ (рис. 26) длины сторон равны длины диагоналей равны $$ {d}_{1}$$ и $$ {d}_{2}: AC={d}_{2}$$, $$ AB=DC=a$$, $$ BD={d}_{1}$$.
Если то Из треугольников $$ ABD$$ и $$ ACD$$ по теореме косинусов будем иметь:
Складывая почленно эти равенства и учитывая, что получим требуемое равенство: .
 |
| Рис. 26 |
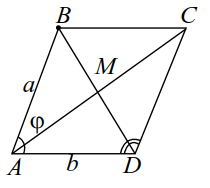
Из решения данной задачи легко получить выражение медианы $$ {m}_{c}$$ треугольника через его стороны $$ a, b$$ и $$ c$$. Пусть в `ABD:AB=a`, `AD=b`, `BD=c`; `AM` - медиана, `AM=m_c` (рис. 26). Достроим этот треугольник $$ ABD$$ до параллелограмма $$ ABCD$$ и воспользуемся результатом задачи 11, получим:
$$ {c}^{2}+{\left(2{m}_{c}\right)}^{2}=2{a}^{2}+2{b}^{2}$$, откуда
.
 |
| Рис. 27 |
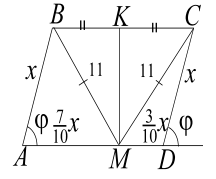
На стороне $$ AD$$ ромба $$ ABCD$$ взята точка $$ M$$, при этом $$ MD={\displaystyle \frac{3}{10}}AD, BM=MC=11.$$ Найти площадь треугольника $$ BCM.$$
1. Обозначим длину стороны ромба $$ x, \angle BAD=\varphi $$
(рис. 27). По условию $$ MD={\displaystyle \frac{3}{10}}x\Rightarrow AM={\displaystyle \frac{7}{10}}x.$$ Из треугольников $$ ABM$$ и $$ MCD$$ по теореме косинусов получаем:
$$ B{M}^{2}={x}^{2}+{\left({\displaystyle \frac{7}{10}}x\right)}^{2}-2x{\displaystyle \frac{7}{10}}x\mathrm{cos}\varphi $$,
$$ M{C}^{2}={x}^{2}+{\left({\displaystyle \frac{3}{10}}x\right)}^{2}-2x{\displaystyle \frac{3}{10}}x\mathrm{cos}(180°-\varphi )$$.
Приравниваем правые части (по условию $$ BM=MC$$), подставляем сокращаем на $$ {x}^{2},$$ приводим подобные члены и получаем $$ \mathrm{cos}\varphi ={\displaystyle \frac{1}{5}}.$$ Подставляя найденное значение $$ \mathrm{cos}\varphi $$ и $$ BM=11$$ в первое равенство, находим $$ x=10$$.
2. В равнобедренном треугольнике $$ BMC$$ основание равно `10`, находим высоту $$ MK$$:
$$ MK=\sqrt{B{M}^{2}-B{K}^{2}}=\sqrt{B{M}^{2}-{\displaystyle \frac{1}{4}}B{C}^{2}}=\sqrt{96}$$,
тогда площадь треугольника `BMC` равна $$ {\displaystyle \frac{1}{2}}BC·MK=20\sqrt{6}$$.
 |
| Рис. 28 |
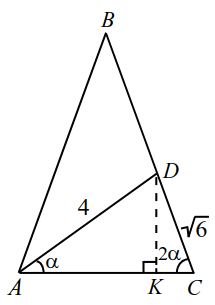
В равнобедренном треугольнике $$ ABC (AB=BC)$$ проведена биссектриса $$ AD$$ (рис. 28). Найти радиус описанной около треугольника $$ ABC$$ окружности, если $$ AD=4$$ и $$ DC=\sqrt{6}.$$
1. Углы при основании $$ AC$$ в треугольнике $$ ABC$$ равны, обозначим $$ \angle BAC=2\alpha ,$$ тогда $$ \angle DAC=\alpha .$$ По теореме синусов из треугольника $$ ADC$$ следует $$ {\displaystyle \frac{4}{\mathrm{sin}2\alpha }}={\displaystyle \frac{\sqrt{6}}{\mathrm{sin}{\displaystyle \alpha }}}$$ откуда $$ \mathrm{cos}\alpha =\sqrt{{\displaystyle \frac{2}{3}}}$$. Находим: $$ \mathrm{cos}2\alpha =2{\mathrm{cos}}^{2}\alpha -1={\displaystyle \frac{1}{3}}$$ и $$ \mathrm{sin}2\alpha ={\displaystyle \frac{2\sqrt{2}}{3}}$$.
2. Вычисляем сторону $$ AC$$:
$$ AC=AK+KC=AD\mathrm{cos}\alpha +DC\mathrm{cos}2\alpha ={\displaystyle \frac{5}{3}}\sqrt{6}$$.
3. Как следует из теоремы синусов, радиус $$ R$$ описанной около треугольника `ABC` окружности может быть найден из равенства:
$$ R={\displaystyle \frac{AC}{2\mathrm{sin}B}}$$ т. е. $$ R={\displaystyle \frac{AC}{2\mathrm{sin}(180°-4\alpha )}}={\displaystyle \frac{AC}{4\mathrm{sin}2\alpha ·\mathrm{cos}2\alpha }}={\displaystyle \frac{15}{8}}\sqrt{3}$$.
В решении следующих задач существенно используется знание тригонометрических тождеств, умение решать тригонометрические уравнения. Подобные задачи не рассматривались в заданиях 9 - 10 классов, поскольку большинство учащихся в то время не обладало знаниями по тригонометрии в достаточном объёме.
В этих задачах в качестве неизвестной выбирается некоторый угол и по данным задачи и известным метрическим соотношениям составляется тригонометрическое уравнение или система уравнений. Их составление и решение является основным этапом всего решения задачи, а искомые элементы определяются через значения тригонометрических функций введённого угла.
 |
| Рис. 29 |
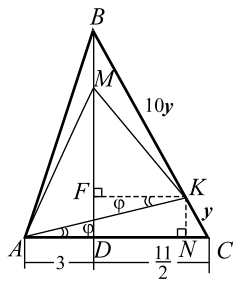
Точки $$ K$$ и $$ M$$ расположены соответственно на стороне $$ BC$$ и высоте $$ BD$$ остроугольного треугольника $$ ABC$$. Треугольник $$ AMK$$ - равносторонний (рис. 29). Найти его площадь, если $$ AD=3$$, $$ DC={\displaystyle \frac{11}{2}}$$, $$ BK:KC=10:1$$.
1. Обозначим сторону правильного треугольника $$ AMK$$ через $$ x, \angle KAC=\varphi $$ (рис. 29). Пусть $$ FK\left|\right|AC$$ и $$ KN\perp AC$$. Из подобия треугольников $$ CKN$$ и $$ CBD$$ следует $$ NC={\displaystyle \frac{1}{11}}DC={\displaystyle \frac{1}{2}}$$. Тогда $$ DN=5, AN=8.$$
2. Заметим, что $$ \angle FKA=\varphi $$ и $$ \angle MKF={\displaystyle \frac{\mathrm{\pi }}{3}}-\varphi $$. Из прямоугольных треугольников $$ AKN$$ и $$ MKF$$ следует:
$$ AN=AK\mathrm{cos}\varphi $$ и $$ FK=MK\mathrm{cos}({\displaystyle \frac{\mathrm{\pi }}{3}}-\varphi )$$, т. е. $$ 8=x\mathrm{cos}\varphi $$ и $$ 5=x\mathrm{cos}({\displaystyle \frac{\mathrm{\pi }}{3}}-\varphi )$$. Из тригонометрического уравнения `5cosvarphi=8cos(pi/3-varphi)` получаем
$$ \mathrm{cos}\varphi =4\sqrt{3}\mathrm{sin}\varphi $$ и $$ \mathrm{tg}\varphi ={\displaystyle \frac{1}{4\sqrt{3}}}$$.
3. По формуле $$ \mathrm{cos}\varphi ={\displaystyle \frac{1}{\sqrt{1+\mathrm{tg}^{2}\varphi }}}$$ находим $$ \mathrm{cos}\varphi ={\displaystyle \frac{4\sqrt{3}}{7}}$$ и $$ x={\displaystyle \frac{8}{\mathrm{cos}\varphi }}={\displaystyle \frac{14}{\sqrt{3}}}$$. Площадь правильного треугольника со стороной $$ x$$ равна $$ {\displaystyle \frac{{x}^{2}\sqrt{3}}{4}}$$. Находим $$ {S}_{AMK}={\displaystyle \frac{49\sqrt{3}}{3}}$$.
Обратим внимание, что в этой задаче один треугольник повёрнут относительно другого. В качестве промежуточной переменной и был введён этот угол поворота.
 |
| Рис. 30 |
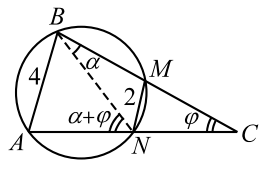
Окружность проходит через вершины $$ A$$ и $$ B$$ треугольника $$ ABC,$$ пресекает стороны $$ BC$$ и $$ AC$$ в точках $$ M$$ и $$ N$$ соответственно (рис. 30). Известно, что `AB=4`, `MN=2`, $$ \angle ACB=\mathrm{arcsin}\frac{3}{5}$$. Найти радиус окружности.
1. Обозначим $$ \angle ACB=\varphi $$ тогда $$ \mathrm{sin}\varphi ={\displaystyle \frac{3}{5}}$$, $$ \varphi $$ - острый угол, $$ \mathrm{cos}\varphi ={\displaystyle \frac{4}{5}}$$.
Надо найти радиус окружности, поэтому разумно ввести вписанный угол: $$ \angle NMB=\alpha $$. Угол $$ ANB$$ - внешний для треугольника $$ BNC,$$ поэтому $$ \angle ANB=\alpha +\varphi $$.
2. Если $$ R$$ - радиус окружности, то $$ AB=2R\mathrm{sin}(\alpha +\varphi )$$, и $$ MN=2R\mathrm{sin}\alpha $$ т. е. получаем систему:
$$ \left\{\begin{array}{l}4=2R\mathrm{sin}(\alpha +\varphi ),\\ 2=2R\mathrm{sin}\alpha .\end{array}\right.$$
Исключая `R`, придём к уравнению $$ 2\mathrm{sin}\alpha =\mathrm{sin}(\alpha +\varphi )$$.
Так как $$ \mathrm{sin}(\alpha +\varphi )=\mathrm{sin}\alpha ·\mathrm{cos}\varphi +\mathrm{sin}\varphi ·\mathrm{cos}\alpha ={\displaystyle \frac{4}{5}}\mathrm{sin}\alpha +{\displaystyle \frac{3}{5}}\mathrm{cos}\alpha $$,
то уравнение приводится к виду
$$ 10\mathrm{sin}\alpha =4\mathrm{sin}\alpha +3\mathrm{cos}\alpha $$, `6sinalpha=3cosalpha`, `"tg"alpha=1/2`.
3. Находим: $$ \mathrm{sin}\alpha ={\displaystyle \frac{\mathrm{tg}\alpha }{\sqrt{1+\mathrm{tg}^{2}\alpha }}}={\displaystyle \frac{1}{\sqrt{5}}}$$ тогда $$ R={\displaystyle \frac{MN}{2\mathrm{sin}\alpha }}=\sqrt{5}$$.
В задаче 15 угловая величина была задана значением $$ \mathrm{arcsin}{\displaystyle \frac{3}{5}}$$. По определению функции $$ y=\mathrm{arcsin}x$$ это означало, что заданный угол острый и $$ \mathrm{sin}\varphi ={\displaystyle \frac{3}{5}}$$. Мы заменили условие $$ \varphi =\mathrm{arcsin}{\displaystyle \frac{3}{5}}$$ равносильным ему. Аналогично следует поступать во всех задачах, условия которых содержат значения обратных тригонометрических функций для величин углов. Например, если угол задан в виде $$ \alpha =\pi -\mathrm{arccos}\sqrt{{\displaystyle \frac{2}{3}}}$$, то это означает, что $$ \alpha $$ - тупой угол, $$ \mathrm{cos}\alpha =-\sqrt{{\displaystyle \frac{2}{3}} }$$, $$ \mathrm{sin}\alpha ={\displaystyle \frac{1}{\sqrt{3}}}$$ и могут быть найдены, если окажется необходимым, значения $$ \mathrm{cos}2\alpha $$, $$ \mathrm{sin}{\displaystyle \frac{\alpha }{2}}$$ и т. п.
Некоторые учащиеся, проводя решение задачи в общем виде и подставляя числовые данные лишь в конце (что, заметим, обычно делает решение громоздким), получают, например, ответ для длины стороны в виде $$ \alpha =3\mathrm{sin}\left(2\mathrm{arccos}{\displaystyle \frac{1}{\sqrt{3}}}\right)$$. Если далее это значение не записано в виде $$ a=2\sqrt{2}$$, то решение не считается доведённым до конца. Т. е. ответ задачи, когда угловая величина задана значением обратной тригонометрической функции, не должен содержать значения тригонометрических и обратных тригонометрических функций (если только сама искомая величина не является углом).
В заключение параграфа решим задачу об определении угла треугольника. Обратим внимание, что решение требует отбора в соответствии с условием задачи.
 |
| Рис. 31 |
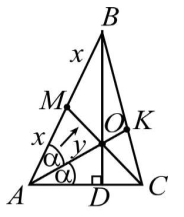
В треугольнике $$ ABC$$ высота $$ BD$$, медиана $$ CM$$ и биссектриса $$ AK$$ пересекаются в точке $$ O$$. (рис. 31). Найти угол $$ A$$, если известно, что он больше $$ 60°$$ и $$ AM=\sqrt{3}OM$$.
1. Обозначим
$$ AM=x$$ (тогда `AB=2x`), $$ \angle BAC=2\alpha $$ и $$ AO=y$$.
Из прямоугольных треугольников $$ AOD$$ и $$ ABD$$ имеем: $$ AD=y\mathrm{cos}\alpha $$ и $$ AD=2x\mathrm{cos}2\alpha $$. Выражаем $$ y={\displaystyle \frac{2x\mathrm{cos}2\alpha }{\mathrm{cos}\alpha }}$$.
2. Применяем теорему косинусов к треугольнику $$ AMO$$, учитывая, что $$ M{O}^{2}={\displaystyle \frac{1}{3}}{x}^{2}: {\displaystyle \frac{{x}^{2}}{3}}={x}^{2}+{y}^{2}-2xy·\mathrm{cos}\alpha $$.
Подставляем выражение для $$ y$$, сокращаем на $$ {x}^{2},$$ приводим уравнение к виду:
$$ 2{\mathrm{cos}}^{2}\alpha +12{\mathrm{cos}}^{2}2\alpha -12\mathrm{cos}2\alpha ·{\mathrm{cos}}^{2}\alpha =0$$.
Используем тождество: $$ 2{\mathrm{cos}}^{2}\alpha =1+\mathrm{cos}2\alpha ,$$ получаем уравнение:
$$ 6{\mathrm{cos}}^{2}2\alpha -5\mathrm{cos}2\alpha +1=0$$.
Находим: $$ \mathrm{cos}2\alpha ={\displaystyle \frac{1}{3}}$$ или $$ \mathrm{cos}2\alpha ={\displaystyle \frac{1}{2}}$$.
3. По условию: $$ 2\alpha =\angle BAC$$, $$ 2\alpha > {\displaystyle \frac{\mathrm{\pi }}{3}}$$, значит $$ \mathrm{cos}2\alpha < {\displaystyle \frac{1}{2}}$$, поэтому
$$ \mathrm{cos}2\alpha =\mathrm{cos}A={\displaystyle \frac{1}{3}}$$, $$ \angle A=\mathrm{arccos}{\displaystyle \frac{1}{3}}$$.

В заключении остановимся на ещё не обсуждавшийся в этом задании вопросе о роли рисунка в решении геометрических задач.
Некоторые учащиеся и абитуриенты ограничиваются небрежным мелким рисунком, на котором даже трудно разобрать, какие обозначения к чему относятся, какие прямые перпендикулярны или параллельны, в каких точках имеет место касание и т. п. Кое-кому из них всё же удаётся верно решить задачу, но в большинстве случаев, особенно в задачах, требующих ряда шагов рассуждений и вычислений, такой рисунок скорее мешает решению, а не способствует успеху.
Рисунок в геометрической задаче – это удобный для восприятия наглядный способ записи условий задачи, фиксирующий и удерживающий внимание решающего, он даёт повод к размышлению и может стать помощником в решении задачи, подсказать правильный путь в поисках решения. (Посмотрите, например, на рис. 27, 28, 29). Именно поэтому к построению рисунка полезно относиться вдумчиво. Сначала, чтобы понять задачу, её условия переводят на геометрический язык: делают от руки небольшой предварительный рисунок и отмечают на нём (если таковые есть) равные углы, пропорциональность отрезков, перпендикулярность и т. п. И лишь обдумав, как надо изменить рисунок, чтобы он соответствовал условиям задачи, делают аккуратный и достаточно большой рисунок, чтобы на нём уместились все введённые обозначения углов, отрезков и данные задачи. В ряде случаев «хороший» рисунок получается не с первой попытки и при его построении уже начинается процесс решения задачи, так как используются определения и известные геометрические факты относительно входящих в условие задачи элементов геометрической конфигурации.
Когда словами записываются геометрические свойства входящих в задачу элементов, устанавливаются метрические соотношения типа и т. п., проводятся некоторые вычисления, то охватить их взглядом, увидеть в целом, сделать нужный вывод бывает совсем непросто, а вот увидеть на рисунке след собственных рассуждений и не терять этого из виду обычно удаётся.
Мы говорим о работе с рисунком в процессе поиска решения. При окончательном изложении решения задачи каждое заключение должно быть обосновано (чаще всего ссылками на известные теоремы курса, реже – дополнительным доказательством). Сам по себе рисунок, даже самый аккуратный, выполненный циркулем и линейкой, ничего не доказывает, всё, что «увидено» из чертежа, должно иметь логическое обоснование.
И ещё одно замечание. Если задача не получается, «упирается», не достаёт ещё какого-то одного соотношения, связи элементов – вернитесь к условию задачи и вновь обсудите каждый входящий в него геометрический элемент. Скорее всего, вами использованы не все их свойства, сделаны не все возможные выводы.
Поясним наши рассуждения о рисунке и работе с ним примерами решения двух задач олимпиад МФТИ.
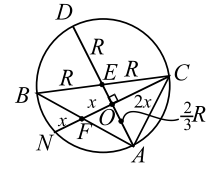
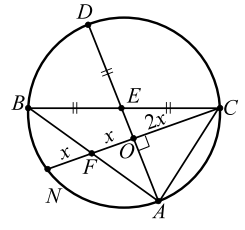
Продолжения медиан $$ AE$$ и $$ CF$$ треугольника $$ ABC$$ (рис. 32) пересекают описанную около него окружность в точках $$ D$$ и $$ N$$ соответственно так, что $$ AD:AE=2:1$$ и $$ CN:CF=4:3.$$ Найти углы треугольника.
 |
| Рис. 32 |
Делаем предварительный рисунок (кстати, его удобнее всего рисовать, начиная с окружности), отмечаем, что (это следует из условия $$ AD=2AE$$). Две хорды $$ BC$$ и $$ AD,$$ пересекаясь, делятся пополам. По свойству пересекающихся хорд $$ AE·DE=BE·CE$$ откуда следует, что $$ AE=BE=DE=CE$$. Точка $$ E$$ одинаково удалена от точек `A`, `B`, `D` и `C` окружности, значит точка $$ E$$ - центр окружности. Отсюда следует, что $$ BC$$ и $$ AD$$ - диаметры, и - прямой (опирается на диаметр). Поскольку далее должна рассматриваться медиана $$ AE,$$ а нами установлено, что $$ AE=DE=BE=CE,$$ то удобно ввести обозначение $$ AE=R.$$
 |
| Рис. 33 |
Обсудим следующие условия задачи: $$ FN={\displaystyle \frac{1}{3}}FC.$$ Обозначим $$ FN=x,$$ тогда $$ FC=3x.$$ Наконец обратим внимание, что в задаче есть две медианы треугольника, значит надо воспользоваться свойством медиан: пересекаясь, они делятся в отношении `2:1`, считая от вершины. Итак, если обозначить через $$ O$$ точку пересечения медиан, то
$$ AO={\displaystyle \frac{2}{3}}R, CO=2x, OF=x.$$
Выполняем хороший большой рисунок с учётом всех установленных фактов. Посмотрим внимательно на рис. 33 и подумаем, может быть, еще что-то можно установить? Да! Хорда $$ CN,$$ пересекая диаметр $$ AD,$$ делится пополам, значит Отразим и этот последний факт.
Теперь решение.
1. По свойству пересекающихся хорд:
$$ AO·OD=CO·ON$$, т. е. $$ {\displaystyle \frac{2}{3}}R\frac{4}{3}R=4{x}^{2}$$ откуда $$ {x}^{2}=\frac{2}{9}{R}^{2}$$.
2. Из прямоугольного треугольника $$ COA$$ по теореме Пифагора:
$$ AC=\sqrt{{\left(2x\right)}^{2}+{\left(\frac{2}{3}R\right)}^{2}}={\displaystyle \frac{2}{\sqrt{3}}}R$$.
3. Из прямоугольного треугольника $$ ABC$$ находим:
$$ \mathrm{sin}B={\displaystyle \frac{AC}{BC}}={\displaystyle \frac{1}{\sqrt{3}}}$$.
$$ \angle A={\displaystyle \frac{\mathrm{\pi }}{2}}$$, $$ \angle B=\mathrm{arcsin}{\displaystyle \frac{1}{\sqrt{3}}}$$, $$ \angle C={\displaystyle \frac{\mathrm{\pi }}{2}}-\mathrm{arcsin}{\displaystyle \frac{1}{\sqrt{3}}}$$.
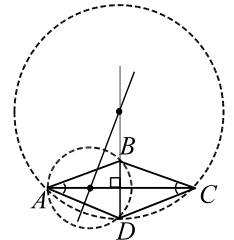
Длина стороны ромба $$ ABCD$$ равна `4`. Расстояние между центрами окружностей, описанных около треугольников $$ ABD$$ и $$ ACD,$$ равно `3`. Найти радиусы окружностей.
Строим первый пробный рисунок (рис. 34) и начинаем рассуждать.
Поскольку в условии задачи задано расстояние между центрами, то необходимо установить их положение. Будем помнить, что четырёхугольник $$ ABCD$$ - ромб, характеризующее его свойство – диагонали, пересекаясь, делятся пополам и перпендикулярны друг другу. Центр окружности, описанной около треугольника, есть точка пересечения серединных перпендикуляров к его сторонам. Треугольники $$ ABD$$ и $$ ACD$$ имеют общую сторону $$ AD$$, следовательно, оба центра лежат на серединном перпендикуляре отрезка $$ AD$$.
Кроме того, центр $$ {O}_{1}$$ окружности, описанной около треугольника $$ ABD,$$ лежит на прямой $$ AC$$ (это серединный перпендикуляр отрезка $$ BD$$), а центр $$ {O}_{2}$$ окружности, описанной около треугольника $$ ACD,$$ лежит на прямой $$ BD$$ (это серединный перпендикуляр отрезка $$ AC$$). Итак, центры окружностей – это точки пересечения серединного перпендикуляра отрезка $$ AD$$ с прямыми $$ AC$$ и $$ BD.$$
 |
 |
| Рис. 34 | Рис. 35 |
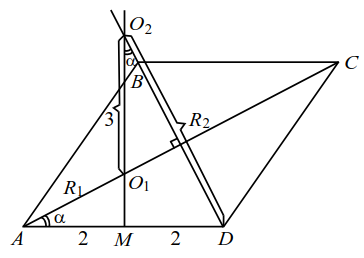
Вот теперь строим новый рисунок, на который наносим также числовые данные задачи. Обратим внимание, что окружности рисовать уже нет необходимости.
Обозначим $$ A{O}_{1}={R}_{1}$$ и $$ D{O}_{2}={R}_{2}$$ и, поскольку имеем несколько подобных треугольников, вводим ещё угол $$ \angle MA{O}_{1}=\alpha .$$ Записываем вполне очевидные выводы:
$$ 1. \overline{)\begin{array}{l}∆A{O}_{1}M, \angle M=90°,\\ \angle MA{O}_{1}=\alpha \end{array}}\Rightarrow \begin{array}{l}2={R}_{1}\mathrm{cos}\alpha ,\\ {O}_{1}M={R}_{1}\mathrm{sin}\alpha .\end{array}$$
$$ 2.\overline{)\begin{array}{l}△D{O}_{2}M: \angle M=90°,\\ \angle M{O}_{2}D=\alpha \end{array}} \Rightarrow \begin{array}{l}2={R}_{2}\mathrm{sin}\alpha ,\\ {O}_{2}M={R}_{2}\mathrm{cos}\alpha .\end{array}$$
$$ 3.\overline{)\begin{array}{l}\mathrm{По} \mathrm{условию} {O}_{1}{O}_{2}=3,\\ \mathrm{т}. \mathrm{е}. {O}_{2}M-{O}_{1}M=3\end{array}} \Rightarrow {R}_{2}\mathrm{cos}\alpha -{R}_{1}\mathrm{sin}\alpha =3.$$
Итак, получили систему из трёх уравнений с тремя неизвестными:
$$ {R}_{1}, {R}_{2}, \alpha : \left\{\begin{array}{l}2={R}_{1}\mathrm{cos}\alpha .\\ 2={R}_{2}\mathrm{sin}\alpha ,\\ 3={R}_{2}\mathrm{cos}\alpha -{R}_{1}\mathrm{sin}\alpha .\end{array}\right.\phantom{\rule{0ex}{0ex}}$$
Решать эту систему можно по-разному, например, исключив `R_1` и `R_2`, получить тригонометрическое уравнение
$$ 3=2{\displaystyle \frac{\mathrm{cos}\alpha }{\mathrm{sin}\alpha }}-2{\displaystyle \frac{\mathrm{sin}\alpha }{\mathrm{cos}\alpha }}$$, $$ 2{\mathrm{tg}}^{2}\alpha +3\mathrm{tg}\alpha -2=0$$, $$ \mathrm{tg}\alpha ={\displaystyle \frac{1}{2}}$$ (угол `alpha` - острый), тогда
$$ \mathrm{cos}\alpha ={\displaystyle \frac{1}{\sqrt{1+\mathrm{tg}^{2}\alpha }}}={\displaystyle \frac{2}{\sqrt{5}}}$$ и $$ {R}_{1}=\sqrt{5}, {R}_{2}=2\sqrt{5}$$
В этой задаче, оказавшейся совсем не простой для абитуриентов, трудность для многих была заключена в построении рисунка, обнажающего условие задачи и направляющего решение.

$$ S={\displaystyle \frac{1}{2}}ah$$ (`a` - основание, `h` - высота к `a`).
$$ S={\displaystyle \frac{1}{2}}ab·\mathrm{sin}C$$ (`a`, `b`- стороны, `C` - угол между ними).
$$ S=\sqrt{p(p-a)(p-b)(p-c)}$$ (формула Герона, $$ 2p=a+b+c)$$.
$$ S=pr$$ (`p` - полупериметр,`r` - радиус вписанной окружности).
$$ S={\displaystyle \frac{abc}{4R}}$$, где `R` - радиус описанной окружности).
$$ S=(p-a){r}_{a}$$, где `p` - полупериметр, `r_a` - радиус вневписанной окружности, касающейся стороны `a`.
$$ S={\displaystyle \frac{a+b}{2}}h$$ (`a`, `b` - основания, `h` - высота).
$$ S=c·m$$ (`c` - боковая сторона, `m` - расстояние до нее от середины другой боковой стороны).
$$ S=ah$$ (`a` - сторона, `h` - высота к `a`).
$$ S=ab·\mathrm{sin}\alpha $$ (`a`, `b` - стороны, `alpha` - величина угла между ними).
$$ S={\displaystyle \frac{1}{2}}{d}_{1}{d}_{2}\mathrm{sin}\varphi $$ (`d_1` и `d_2` - диагонали, `varphi` - величина угла между ними).
$$ {d}_{1}^{2}+{d}_{2}^{2}=2({a}^{2}+{b}^{2})$$ (`a` и `b` - стороны,`d_1`, `d_2` - диагонали).
$$ {m}_{c}^{2}={\displaystyle \frac{{a}^{2}+{b}^{2}}{2}}-{\displaystyle \frac{{c}^{2}}{4}}$$
1) $$ AD={\displaystyle \frac{2bc}{b+c}}\mathrm{cos}{\displaystyle \frac{A}{2}}, \left(b=AC, c=AB\right)$$.
2) $$ AD=\sqrt{bc-xy}, (x=BD, y=DC, {\displaystyle \frac{x}{y}}={\displaystyle \frac{c}{b}})$$.
$$ {d}^{2}={c}^{2}+ab$$ (`a`, `b` - основания, `c` - боковая сторона, `d` - диагональ).

В восьмом и девятом классах ЗФТШ было по два Задания по геометрии. Напомним, что были повторены темы: равенство и подобие треугольников, свойства параллелограммов, прямоугольный треугольник, свойства биссектрис, медиан и высот треугольника, теорема Менелая, свойства касательных хорд и секущих, площадь треугольника и четырёхугольника.
Как и раньше, основное внимание уделяется приёмам решения задач. Подробные решения 19 задач демонстрируют различные методы и подходы, по ходу решения напоминаются теоремы и свойства фигур, при этом отобраны в определённом смысле характерные задачи по каждой теме; в некоторых задачах доказаны новые утверждения и получены полезные формулы.
Задание оканчивается контрольными вопросами и задачами для самостоятельного решения. Приступая к решению задания, сначала ознакомьтесь с нашими пожеланиями и требованиями по его оформлению и с примерами ответов на контрольные вопросы (этот материал размещён перед контрольными вопросами). Вопросы и задачи оценены по трудности в очках, указанных в скобках после номера. За правильный ответ и верное решение ставится полное число очков, за недочёты или ошибки определённое число очков снимается. Знаком (`**`) звёздочка отмечены более трудные задачи и вопросы.
Для тех, кто лишь в этом году поступил в ЗФТШ, сделаем дополнительные замечания. Работа над заданием потребует определённого времени. Надо прочитать и проработать каждый параграф: разобрать приведённые доказательства, выучить формулировки теорем, выписать и запомнить формулы. И, что очень важно, понять и воспроизвести решения приведённых в тексте примеров. После этого вы легко ответите на большинство контрольных вопросов и решите предложенные задачи.
Кроме того, рекомендуем найти на сайте ЗФТШ Задания №1 и №5 для 9-го класса, прочитать их, разобрать новые для Вас утверждения, формулы, (которые выучить), методы. Именно для тех, кто поступил в ЗФТШ в этом году, данное Задание и Задание №5 для 9 класса имеют пересечение - т. е. некоторые части текста у них одинаковые.
Задачи для самостоятельного решения различной сложности. Если какую-либо задачу не удалось решить, найдите аналогичную в тексте задания, разберите её и сделайте ещё одну попытку. Либо подумайте, на какую тему задача и какой параграф следует ещё раз повторить из этого Задания или Заданий для 9-го класса.

Для произвольного треугольника, длины сторон которого, противолежащие вершинам `A`, `B` и `C`, обозначим `a`, `b` и `c`, справедливы две теоремы, устанавливающие соотношения между сторонами и углами треугольника. Утверждения этих теорем кратко можно записать так:
`c^2=a^2+b^2-2abcosC`
`a/(sinA)=b/(sinB)=c/(sinC)`
Напомним также, что
`a/(sinA)=b/(sinB)=c/(sinC)=2R` (1)
где `R` - радиус окружности, описанной около треугольника.
Покажем применение этих теорем.
В параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его сторон.
Пусть `ABC` - параллелограмм и `AB=CD=a`, `AD=BC=b`, `BD=d_1`, `AC=d_2`, (рис. 1). Если `varphi=/_BAD`, то `/_ADC=180^@-varphi`. Из треугольников `ABD` и `ACD` по теореме косинусов будем иметь:
`d_1^2=a^2+b^2-2abcosvarphi`,
`d_2^2=a^2+b^2-2abcos(180^@-varphi)`.
Складывая почленно эти равенства и учитывая, что `cos(180^@-varphi)=-cosvarphi`, получим требуемое равенство:
| `d_1^2+d_2^2=2a^2+2b^2`. |
Зная три стороны треугольника `a`, `b` и `c`, найти медиану `m_c` к стороне `c`.
Пусть в треугольнике `ABD` (рис. 1) `AB=a`, `AD=b`, `BD=c` и `AO` - медиана. Достроим треугольник `ABD` до параллелограмма (на прямой `AO` отложим `OC=AO` и соединим точки `B` с `C` и `D` с `C`; диагонали четырёхугольника `ABCD`, пересекаясь, делятся пополам, это параллелограмм). Так как `BD=c` и `AC=2m_c`, то по доказанному в теореме 1 имеем: `(2m_c)^2+c^2=2a^2+2b^2`; отсюда получаем формулу для медианы треугольника через его стороны:
| `m_c=sqrt((a^2+b^2)/2-c^2/4)`. |
В треугольнике `ABC` точки `M` и `N` лежат на сторонах `AB` и `AC` (рис. 2), при этом `BM=MN=NC`. Найти отношение `MN:BC`, если `AC:AB = 3:2`, и угол `A` равен `60^@`.
Обозначим `x=MN`, `2a=AB`, тогда `AC=3a`, `ul(AM=2a-x)` и `ul(AN=3a-x)`. Применим теорему косинусов к треугольнику `AMN`, в котором стороны выражены через `a` и `x` и известен угол `/_MAN=60^@`, получим `x^2=(2a-x)^2+(3a-x)^2-(2a-x)(3a-x)`, откуда находим `x=7/5 a`. По теореме косинусов выразим сторону `BC` через `a`:
`BC=sqrt(AB^2+AC^2-2AB*ACcos60^@)=sqrt7a`.
Теперь находим `(MN)/(BC)=x/(BC)=(sqrt7)/5`.
`(MN)/(BC)=(sqrt7)/5`.
Обратим внимание на применение теоремы косинусов. При доказательстве теоремы 1 использовался тот факт, что в фигуре (параллелограмме) есть дополнительные углы `/_A=varphi`, `/_D=180^@-varphi`, а `cos(180^@-varphi)=-cosvarphi`,
В примере 2 теорема косинусов применялась к треугольнику `AMN` с заданным углом `60^@`, стороны которого выражались через заданную величину `a` и неизвестную `x`.
В примере 5 (см. далее) Теорема косинусов позволяет найти косинус угла треугольника по трём известным его сторонам.
Следующие два примера на применение теоремы синусов.
В равнобедренном треугольнике `ABC` длины боковых сторон `AB` и `AC` равны `b`, а угол при вершине `A` равен `30^@` (рис. 3). Прямая, проходящая через вершину `B` и центр `O` описанной окружности, пересекает сторону `AC` в точке `D`. Найти длину отрезка `BD`.
Центр описанной около треугольника окружности лежит на серединном перпендикуляре `OK`, но т. к. высота равнобедренного треугольника является и медианой, то т. `O` лежит на высоте `AK`, которая является также и биссектрисой угла `A`. Таким образом,
`/_BAK=/_CAK=15^@`.
Треугольник `AOB` равнобедренный: `(AO=OB)` следовательно, `/_ABO=/_BAO=15^@`. Итак, в треугольнике `ABD` известны два угла, а т. к. сумма углов треугольника равна `180^@`, то `/_BDA=135^@`. По теореме
синусов из треугольника `ABD` имеем: `(BD)/(sin/_BAD)=(AB)/(sin/_BDA)`, откуда, учитывая, что `sin135^@=sin45^@`, находим:
`BD=b(sin30^@)/(sin45^@)=b/(sqrt2)`.
Точка `M` лежит на окружности с диаметром `BD`; точки `A` и `C` лежат на прямой `BD`, точка `C` лежит внутри окружности, а точка `B` - между точками `A` и `C`. Известно, что `AB=a`, `BC=b` и `/_AMB=/_BMC` (рис. 4). Найти радиус окружности.
1. Обозначим равные углы `AMC` и `BMC` через `alpha`, `BD=2R`, проведём хорду `MD` и обозначим `/_ADM=varphi`.
Угол `BMD` прямой (опирается на диаметр), тогда `/_AMD=90^@+alpha`, а `/_CMD=90^@-alpha`.
Применим теорему синусов к треугольникам `AMD` и `CMD`:
$$ \begin{array}{l}{\displaystyle \frac{AM}{\mathrm{sin}}}={\displaystyle \frac{AD}{\mathrm{sin}{\displaystyle \left(90°+\alpha \right)}}}\iff {\displaystyle \frac{AM}{\mathrm{sin}{\displaystyle \phi }}}={\displaystyle \frac{2R+a}{\mathrm{cos}{\displaystyle \alpha }}}\\ {\displaystyle \frac{CM}{\mathrm{sin}}}={\displaystyle \frac{CD}{\mathrm{sin}{\displaystyle \left(90°-\alpha \right)}}}\iff {\displaystyle \frac{CM}{\mathrm{sin}{\displaystyle \phi }}}={\displaystyle \frac{2R-b}{\mathrm{cos}{\displaystyle \alpha }}}\end{array}>\iff {\displaystyle \frac{AM}{CM}}={\displaystyle \frac{2R+a}{2R-b}}.$$
2. По условию отрезок `MB` - биссектриса угла `AMC`, по свойству биссектрисы `(AM)/(CM)=(AB)/(BC)=a/b`.
Из равенства
`(2R+a)/(2R-b)=a/b iffR=(ab)/(a-b)`.
`R=(ab)/(a-b)`.
Заметим, что из формулы (1) следует тот факт, что радиус окружности, описанной около треугольника, определяется одной из сторон и величиной противолежащего угла, а именно
| `R=a/(2sinA)`. |
Это замечание поможет нам решить следующую задачу.
Из одной точки окружности проведены две хорды `AB` и `BC` длиной `9` и `17`. Отрезок `MN`, соединяющий середины этих хорд, равен `5` (рис. 5). Найти радиус окружности.
По теореме косинусов из треугольника `MBN` найдём
`cos/_B:(MB=9//2, BN=17//2):` `MN^2=MB^2+BN^2-2BM*BNcosB`,
откуда `cosB=(BM^2+BN^2-MN^2)/(2BM*BN)=15/17`.
Значит, `sin/_B=sqrt(1-cos^2B)=8/17`. Далее, т. к. `MN` - средняя линия треугольника `ABC`, то `AC=10` и `R=(AC)/(2sinB)=85/8`.
`10,625`.

В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
Пусть `A`, `B` и `C` - углы треугольника`ABC`; `a`, `b` и `c` - противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` - высоты к этим сторонам; `r` - радиус вписанной окружности;`R` - радиус описанной окружности; `2p=(a+b+c)` - периметр треугольника; `S` - площадь треугольника
| `S=1/2ah_a=1/2bh_b=1/2ch_c`, | (1) |
| `S=1/2 ab sinC=1/2acsinB=1/2bcsinA`, | (2) |
| `S=pr`, | (3) |
| ``S=sqrt(p(p-a)(p-b)(p-c))` - формула Герона, | (4) |
| `S=(abc)/(4R)`. | (5) |
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
|
|
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
`R=(abc)/(4S)=(13*14*15)/(4*84)=65/8=ul(8,125)`.
Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь - найти косинус, например, угла `M`. По теореме косинусов
`13=14+15-2sqrt(14)*sqrt(15)cosM iffcosM=8/(sqrt(14)*sqrt(15))`,
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
`S_(KML)=1/2KM*LMsinM=1/2*(sqrt(14)*sqrt(15)*sqrt(146))/(sqrt(14)*sqrt(15))=(sqrt(146))/2`,
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.{1}^{○}$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
`(S_(DBC))/(S_(ABC))=(DC)/(AC)`.
$$ 2.{2}^{○}$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
`(S_(KBL))/(S_(ABC))=(BK*BL)/(BA*BC)`.
$$ 2.{3}^{○}$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC~DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` - точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Точка `M` - середина стороны `BC` (рис. 7б), по утверждению $$ 2.{1}^{○}$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.{1}^{○}$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.
`S_(BOM)=1/3(1/2S)=1/6S`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.{1}^{○}$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).
2. Через точку `D` проведём прямую `DL``|\|``AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL``|\|``AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK``|\|``DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
`22/45`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
Пусть `O` - точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
Итак, `S=3`, `S_1=8`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` - площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.
| `S_(m_am_bm_c)=3/4S_(abc)`. |
Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` - середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
`S=pr=(14+1)*sqrt3=15sqrt3`.
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
| `x=(2ab)/(a+b)cos varphi/2`. |
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` - точки касания, то `I_aD=I_aF=I_aE=r_a`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
`S_(ABC)=S_(ABI_a)+S_(ACI_a)-S_(BCI_a)=1/2 cr_a+1/2br_a-1/2ar_a=`
`=r_a (c+b-a)/2=r_a(2p-2a)/2=r_a(p-a)`.
Итак,
| `S_(ABC)=r_a(p-a)`. |

В школьном учебнике выведены следующие формулы площади параллелограмма:
`S=a*h_a=b*h_b`, (6)
`S=a*bsinvarphi` (7)
Где `a` и `b` - стороны параллелограмма, `h_a` и `h_b` - высоты к ним, `varphi` - величина угла между сторонами параллелограмма.
Докажем теорему о площади четырёхугольника.
Площадь выпуклого четырёхугольника равна половине произведения диагоналей на синус угла между ними, т. е
`S=1/2d_1d_2sinalpha` (8)
где `d_1` и `d_2` - диагонали четырёхугольника, `alpha` - величина угла между ними.
`ABCD` - выпуклый четырёхугольник, диагонали которого `AC` и `BD` пересекаются в точке `O` под углом `alpha` (рис. 15). Через вершины `A` и `C` проведём прямые, параллельные диагонали `BD`, а через вершины `B` и `D` проведём прямые, параллельные диагонали `AC`. Проведённые прямые в пересечении образуют параллелограмм со сторонами, равными диагоналям `BD` и `AC`, и углом `alpha`. Площадь параллелограмма равна `AC*BD*sinalpha`, а площадь четырёхугольника `ABCD` равна, как легко видеть, половине его площади, т. е.
`S_(ABCD)=1/2AC*BD*sinalpha`.
Площадь ромба равна половине произведения его диагоналей. Это сразу следует из доказанной формулы, т. к. диагонали ромба перпендикулярны.
Найти площадь параллелограмма, стороны которого равны `a` и `b` `(a!=b)`, а угол между диагоналями равен `alpha(alpha<90^@)`.
Пусть `O` - точка пересечения диагоналей параллелограмма `ABCD` (рис. 16), `AB=a`, `AD=b`. Обозначим `BD=2x`, `AC=2y`.
Применим теорему косинусов к треугольникам`AOB` и `AOD` (заметим, что `/_AOD=180^@-alpha)`, будем иметь: `a^2=x^2+y^2-2xycosalpha`, `b^2=x^2+y^2+2xycosalpha`. По теореме 3 площадь `S` параллелограмма `ABCD` будет равна `1/2AC*BDsinalpha=2xysinalpha`. Заметим, что это выражение легко можно найти, не определяя `x` и `y` из системы. Действительно, из двух уравнений для `x` и `y` получим `b^2-a^2=4xycosalpha`. По условию `b!=a`, следовательно, `cosa!=0` и `xy=(b^2-a^2)/(4cosalpha)`. Выражаем площадь параллелограмма по формуле (8):
`S=2xysinalpha=(b^2-a^2)/2 "tg"alpha`.
Середины сторон выпуклого четырёхугольника `ABCD` являются вершинами другого четырёхугольника (четырёхугольника Вариньона). Доказать, что четырёхугольник Вариньона - параллелограмм и его площадь равна половине площади `S` четырёхугольника `ABCD`.
1. Проведём диагонали `AC` и `BD`. Середины сторон обозначим `K`, `L`, `M` и `N` (рис. 17). По определению `KL` - средняя линия треугольника `ABC`, по теореме о средней линии `KL``|\|``AC`, `KL=1/2AC`.
Аналогично, `NM` - средняя линия треугольника `ADC`, `NM``|\|``AC`, `NM=1/2AC`.
В четырёхугольнике `KLMN` противоположные стороны `KL` и `NM` равны и параллельны, по признаку `KLMN` - параллелограмм.
Если рассмотреть стороны `LM` и `KN`, то точно также установим, что `LM``|\|``BD``|\|``KN` и `LM=KN=1/2BD`.
2. Из параллельности `KL``|\|``AC` и `KN``|\|``BD` следует, что угол `LKN` параллелограмма `KLMN` равен углу между диагоналями четырёхугольника `ABCD` (обозначим угол `alpha`).
Имеем `S_(KLMN)=KL*KNsinalpha=1/2AC*1/2BDsinalpha`, а по теореме 3
`S_(ABCD)=1/2AC*BD*sinalpha`.
Из этого следует `S_(KLMN)=1/2S_(ABCD)`, ч. т. д.
Рассмотрим несколько задач, где определяется или используется площадь трапеции. Напомним,
что площадь трапеции равна произведению полусуммы оснований на её высоту, т. е.
`S=(a+b)/2h`. (9)
Найти площадь трапеции, если её основания равны `16` и `44`, а боковые стороны равны `17` и `25`.
Через вершину `C` проведём `CK``|\|``BA` (рис. 18). `ABCK` - параллелограмм, его противоположные стороны равны, поэтому в треугольнике `KCD` определяются все стороны: `KC=AB=25`, `CD=17`, `KD=AD-BC=28`.
По формуле Герона вычисляем площадь этого треугольника: `p=36`, `S_(KCD)=210`.
С другой стороны, `S_(KCD)=1/2KD*CF`, если `CF_|_AD`. Отсюда находим `CF=(2S_(KCD))/(KD)=15` и вычисляем площадь трапеции
`S_(ABCD)=1/2(BC+AD)CF=450`.
Отрезок длины `m`, параллельный основаниям трапеции, разбивает её на две трапеции (рис. 19). Найти отношение площадей этих трапеций, если основания трапеции равны `a` и `b` `(b < a)`.
Пусть `BC=b`, `AD=a` и `MN=m`, и `MN``|\|``AD`. Проведём `CE``|\|``BA` и `NF``|\|``BA`, а также `CK_|_MN` и `NP_|_AD`. Обозначим `CK=h_1`, `NP=h_2`. Далее, т. к. `CE``|\|``NF`, то `/_ECN=/_FND`, а из `MN``|\|``AD` следует `/_ENC=/_FDN`. Следовательно, треугольники `ECN` и `FND` имеют по два равных угла, они подобны. Из подобия имеем `(EN)/(FD)=(CN)/(ND)`. Прямоугольные треугольники `KCN` и `PND` также подобны и `(CK)/(NP)=(CN)/(ND)`, поэтому `(EN)/(FD)=(CK)/(NP)`, т. е. `(m-b)/(a-m)=(h_1)/(h_2)`. Если `S_1` и `S_2` - площади трапеций `MBCN` и `AMND`, то
`S_1=1/2(b+m)h_1`, `S_2=1/2(a+m)h_2`
и
`(S_1)/(S_2)=((m+b)h_1)/((a+m)h_2)=(m^2-b^2)/(a^2-m^2`.

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.{1}^{○}$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям - подобны.
$$ 4.{2}^{○}$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.{3}^{○}$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.{4}^{○}$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.{5}^{○}$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.{6}^{○}$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.{7}^{○}$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.{8}^{○}$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
$$ 4.{9}^{○}$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` - диагональ, `c` - боковая сторона, `a` и `b` основания.
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.{10}^{○}$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.{11}^{○}$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Докажем, например, утверждение $$ 4.{9}^{○}$$.
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Складывая, получаем
`d_1^2+d_2^2=a^2+b^2+c_2^2+(c_2^2-2(a-b)c_2cosvarphi)`. (2)
Проводим `CK``|\|``BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
`d_1^2+d_2^2=a^2+b^2+c_2^2+(c_1^2-(a-b)^2)=`
`=(a^2+b^2+c_2^2)+(c_1^2-a^2-b^2+2ab)`.
Окончательно имеем
| `d_1^2+d_2^2=c_1^2+c_2^2+2ab`. |
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
| `d^2=c^2+ab`. |
.
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.{2}^{○}$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` - его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` - её точка пересечения с прямой `BC` (рис. 30б).
По построению `ACKD` - параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`
(т. к. угол `BDK` - это угол между диагоналями трапеции).
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
`S_(BDK)=1/2BK*DP=1/2(BC+AD)DP=S_(ABCD)`.
Итак, `S_(ABCD)=S=24`.
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Пусть `BC=a`, `AD=b`, и пусть `h` - высота трапеции (рис. 31). По свойству $$ 4.{1}^{○}$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
`S_1+S_2+2S_0=(sqrt(S_1)+sqrt(S_2))^2`.
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Трапеция равнобокая, по свойству $$ 4.{11}^{○}$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.{6}^{○}$$
`AK=(AD-BC)/2=1`, `KD=(AD+BC)/2=9`.
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
`R=(3sqrt(10))/(2*3//sqrt(10)) =5`.
$$ 4.{12}^{○}$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.
$$ 4.{13}^{○}$$. Если `S_1` и `S_2` - площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.
$$ 4.{14}^{○}$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` - какая-то сторона (или диагональ трапеции), `alpha` - смотрящий на неё вписанный угол.

Прежде чем приступать к его выполнению, ознакомьтесь с нашими пожеланиями и требованиями.
1. За краткий ответ «да», «нет», «не может быть» без пояснений (доказательство, опровергающий пример) ставится `0` очков. Примеры ответов приведены далее.
2. Если в решении длина какого-либо отрезка выразилась иррациональным числом (например, `a=sqrt5`), то ни в дальнейших вычислениях, ни в ответе не следует заменять это точное значение на приближённое.
3. Если в решении использовалась тригонометрия и получилось, например, `sin alpha=(2sqrt2)/3`, то не следует определять величину угла `alpha` по таблице или на калькуляторе приближённо и затем тем же способом находить значение `cos alpha`, `sin2alpha`, `sin(alpha+45^@)` и т. п. Все значения других тригонометрических функций определяются только по формулам. Например, `cos alpha=-sqrt(1-sin^2 alpha)=-1/3`, если угол `alpha` тупой, и `sin alpha=(2sqrt2)/3`, а
`sin(alpha+45^@)=sin alpha*cos45^@+cos alpha*sin 45^@=(sqrt2)/2(sin alpha+cos alpha)`.
4. Если в Задании контрольный вопрос сопровождается поясняющим рисунком, при ответе перенесите рисунок с теми же обозначениями в свою тетрадь, – это облегчит Вашему педагогу проверку работы.
5. Рисунок к задаче должен быть достаточно большим и ясным, чтобы на нём уместились все введённые Вами обозначения углов, отрезков и данные задачи (посмотрите на рис. 4, 8(а, б) или рис. 30(а, б, в) Задания: как хороший рисунок и обозначения помогают увидеть простое решение).
6. Стремитесь к тому, чтобы Ваше решение было кратким, но обоснованным, и было ясным и понятным для проверяющего (работа проверяется без Вас, Вы не можете комментировать, что же имелось в виду или почему такое равенство имеет место). Для этого полезно решение разбивать на шаги: 1)…, 2)…, 3)… и то, что вычислено или выражено и важно для дальнейшего, выделить, например, так или .
Кроме того, вычисления разумно (а математика – это здравый смысл) проводить в кратких обозначениях, например
`(h_1)/(h_2)=(m-b)/(a-m)`, а не `((CK)/(NP)=((MN-ME)/(AD-MF))`
или `c_1^2=(a-b)^2+c_2^2-2(a-b)c_2 cos varphi`,
(а не `CK^2=(AD-BC)^2-2(AD-BC)*CD*cos(/_ADC)`).
Примеры ответов на контрольные вопросы
Вопрос. Можно ли внутри прямоугольного треугольника с катетами `3` и `4` поместить круг площадью `25//8`?
Ответ: Да, можно. Докажем это.
В прямоугольном треугольнике с катетами `a` и `b` и гипотенузой `c` радиус `r` вписанной окружности выражается формулой `r=(a+b-c)/2` (рисунок 33 напоминает доказательство).
При `a=3`, `b=4` находим `c=5`, `r=1`. Площадь вписанного круга равна `pir^2=pi`; так как `25/8<(25,04)/8<3,13<3,14<pi`, то радиус `r_0` круга площадью `25//8` меньше `1`. Он помещается внутри вписанного круга (если совместить их центры) и, следовательно, внутри треугольника.
Вопрос. Какое наибольшее число острых углов может иметь выпуклый `n`- угольник при `n>3`?
Ответ: Три. Докажем это.
Из вершины (например `A_1`) выходит `(n-1)` отрезков, два из них `(A_1A_2` и `A_1A_n)` - стороны, остальные `(n-3)` - диагонали (рис. 34). Выпуклый `n`- угольник разбивается диагоналями на `(n-2)` треугольника.
Сумма углов каждого треугольника равна `180^@`, значит сумма всех углов выпуклого `n` - угольника равна `180^2(n-2)`.
Сумма углов внутренних и внешних (по одному при каждой вершине) очевидно равна `180^2 *n`, тогда сумма внешних углов равна `180^@ *n-180^@(n-2)=360^@` (!).
Наглядно: если приложить вектор к стороне `A_1A_2` и обойти по периметру `n` - угольник, двигая вектор, то вернувшись на сторону `A_1A_2`, обнаружим, что, сделав полный поворот, вектор принял прежнее положение. Угол поворота вектора равен сумме внешних углов.
Если предположить, что в выпуклом `n` - угольнике `(n>3)` хотя бы `4` острых угла, то сумма их внешних углов (они тупые) будет больше `90^@ *4=360^@`, что не может быть. Значит острых углов не более трёх.
Вопрос. Треугольники `A_1B_1C_1` и `ABC` таковы, что `a_1<a`, `b_1<b`, `c_1<c`. Верно ли, что площадь треугольника `A_1B_1C_1` меньше площади треугольника `ABC`.
Ответ: Нет. Приведём пример (рис. 35).
Рассмотрим два равнобедренных треугольника: `ul(Delta ABC)`, в котором `AC=BC=a`, `/_ACB=150^@`,
`AB=sqrt(a^2+a^2+2a^2(sqrt3)/2) =asqrt(2+sqrt3)`, `S_(ABC)=1/2 a^2 sin150^@=(a^2)/4`;
`DeltaA_1B_1C_1`, в котором `A_1C_1=B_1C_1=sqrt(3/4)a<a`, `/_A_1C_1B_1=90^@`,
`A_1B_1=(sqrt(3/4)a)sqrt2=sqrt(3/2)a<sqrt2a<sqrt(2+sqrt3)a=AB`,
а `S_(A_1B_1C_1)=1/2(sqrt(3/4)a)^2=3/8a^2>1/4a^2=S_(ABC)`.

Бесконечной числовой последовательностью (или просто последовательностью) называется числовая функция `x=x(n)`, определённая на множестве `N` натуральных чисел.
Аргумент `n` этой функции записывается в виде индекса, т. е. вместо записи `x(n)` используют запись `x_n`, а саму последовательность часто обозначают `(x_n)`. Число `x_n` называют `n`-м (читается: энным) членом последовательности `(x_n)`. Задать последовательность означает задать правило, по которому каждому натуральному `n` сопоставляется действительное число `x_n`. Приведём примеры.
(1) `1`; `1`; `1`; `...` (т. е. `x_n=1` для всех `n in N`);
(2) `1^2`; `2^2`; `3^2`; `...` (т. е. `x_n=n^2` для всех `n in N`);
(3) `1`; `1/2`; `1/3`; `...` (т. е. `x_n=1/n` для всех `n in N`);
(4) последовательность, `n`-й член которой равен `n`-му знаку после запятой в десятичной записи числа `8/33`;
(5) последовательность, `n`-й член которой равен количеству простых чисел, не превосходящих `n`;
(6) `x_1=1`, `x_2=1`, `x_n=x_(n-1)+x_(n-2)` для всех `n>=3` (последовательность Фибоначчи).
Как видим, последовательности задаются различными способами. Например, указывается формула `n`-го члена (примеры (1) – (3)). Закон соответствия между номером `n` и членом `x_n` может быть описан словесно (примеры (4) – (5)). Последовательность может быть также задана рекуррентным соотношением: даны несколько первых членов последовательности и формула, выражающая следующие члены последовательности через предыдущие (пример (6)).
Легко убедиться, что в примере (4) `x_1=2`, `x_2=4` `x_3=2`, `x_4=4` и т. д., т. е. `x_n=3+(-1)^n`. В примере (6) формулу `n`-го члена найти сложнее:
`x_n=1/sqrt5(((1+sqrt5)/2)^n-((1-sqrt5)/2)^n)`.
А вот явную формулу `n`-го члена последовательности (5) написать невозможно. Тем не менее, многие её свойства установлены и без формулы.
Напомним два важных примера числовых последовательностей: арифметическая и геометрическая прогрессии. Геометрическая прогрессия – последовательность, заданная рекуррентно соотношением `x_(n+1)=x_nq`, первым членом `x_1!=0` и знаменателем `q!=0`. Арифметическая прогрессия – последовательность, заданная равенством `x_(n+1)=x_n+d` и первым членом `x_1`.
Найти формулу `n`-го члена последовательности, заданной рекуррентно:
`x_1=1/2`; `x_(n+1)=2x_n+1,ninN`.
Рассмотрим вспомогательную последовательность `y_n=x_n+a`, где число `a` подбирается так, чтобы последовательность `y_n` была геометрической прогрессией. Подставляя `x_n=y_n-a` и `x_(n+1)=y_(n+1)-a` в рекуррентное соотношение, имеем `y_(n+1)-a=2(y_n-a)+1`, т. е. `y_(n+1)=2y_n+(1-a)`. Последовательность `y_n` будет геометрической прогрессией, если `1-a=0`, т. е. `a=1`. Поскольку `y_1=x_1+a=3/2`, формула общего члена геометрической прогрессии `y_n`запишется так:
`y_n=3/2 2^(n-1)` `(y_1=3/2, q=2)`.
Тогда `x_n=y_n-a=3*2^(n-2)-1`, `n>=2`.
`x_n=3*2^(n-2)-1,n>=2`.
Каким общим свойством обладают последовательности (1), (2), (5) и (6)?
Каждый их член, начиная со второго, не меньше предыдущего.
Последовательность `(x_n)` называется строго возрастающей, если каждый её член, начиная со второго, больше предыдущего, т. е. `x_(n+1)>x_n` для любого `ninN`. Последовательность `(x_n)` называется строго убывающей, если `x_(n+1)<x_n` для любого `ninN`. Последовательность `(x_n)` называется нестрого убывающей, если `x_(n+1)<=x_n` для любого `ninN`. Последовательность `(x_n)` называется нестрого возрастающей, если `x_(n+1)>=x_n` для любого `ninN`.
Все такие последовательности (строго возрастающие, строго убывающие, нестрого убывающие, нестрого возрастающие) называются монотонными.
Выяснить, является ли монотонной последовательность `x_n=(3n)/(n+2)`.
Уточним, чему равен `x_(n+1)`. Для этого вместо `n` в `x_n=(3n)/(n+2)` подставим `n+1`, т. е. `x_(n+1)=(3(n+1))/(n+3)`. Рассмотрим разность
`x_(n+1)-x_n=(3(n+1))/(n+3)-(3n)/(n+2)=(3[(n+1)(n+2)-n(n+3)])/((n+2)(n+3))=`
`=6/((n+2)(n+3))>0`,
значит, `x_(n+1)>x_n` для любого `n in N`. По определению последовательность `(x_n)` является строго возрастающей.
Приведённые рассуждения являются стандартными при доказательстве монотонности последовательности. Используя особенности последовательности `(x_n)`, можно установить её возрастание более простым способом. Запишем `x_n` в виде
`x_n=(3n+6-6)/(n+2)=3-6/(n+2)`, тогда `x_(n+1)=3-6/(n+3)>3-6/(n+2)=x_n`.
Выяснить, является ли монотонной последовательность `x_n=3+(-1)^n`.
Последовательность не является монотонной, поскольку `x_(2m-1)=2<4=x_(2m)` и `x_(2m)=4>2=x_(2m+1)` для всех натуральных `m`.
Каким общим свойством обладают последовательности (1), (3) и (4)?
Все их члены лежат на отрезке `[0;4]`.
Последовательность `(x_n)` называется ограниченной, если существует число `C>0` такое, что для любого натурального `n` выполняется неравенство `|x_n|<=C`.
Доказать, что последовательность `(x_n)` является ограниченной тогда и только тогда, когда все её члены лежат на некотором отрезке.
Пусть последовательность `(x_n)` ограничена. Тогда существует число `C>0` такое, что `|x_n|<=C` для любого `ninN`. Последнее неравенство можно переписать в виде `-C<=x_n<=C`, т. е. `x_n in[-C;C]`. Обратно, пусть все члены `(x_n)` лежат на некотором отрезке `[m;M]`. Выберем невырожденный симметричный отрезок `[-C;C]`, содержащий `[m;M]`, тогда `-C<=x_n<=C` и, следовательно, `|x_n|<=C`. В качестве такого `C` можно взять, например, `C=max{|m|,|M|}+1`.
Выяснить, является ли ограниченной последовательность `x_n=(10(-1)^n n)/(n^2+1)`.
Рассмотрим `|x_n|=(10n)/(n^2+1)`. Поскольку при уменьшении знаменателя положительной дроби значение дроби увеличивается, имеем:
`|x_n|=(10n)/(n^2+1) <(10n)/(n^2)=10/n<=10`.
Значит, `|x_n|<=10` для любого `ninN`. По определению последовательность `(x_n)` является ограниченной.
Выяснить, является ли ограниченной последовательность `x_n=n^2`.
Предположим, что последовательность `(x_n)` является ограниченной. Это означает, что существует такое число `C>0`, что при всех `ninN` выполняется неравенство `|n^2|<=C`. Однако при `n>sqrt(C+1)` неравенство не выполняется. Следовательно, предположение неверно, т. е. последовательность `(x_n)` не является ограниченной.

При увеличении `n` члены последовательности `x_n=1//n` становятся сколь угодно малыми, неограниченно приближаются (стремятся) к нулю. Логично считать, что ноль - предел последовательности `x_n`. Однако такого интуитивного понимания в более сложной ситуации может оказаться недостаточно. Мы должны точно сформулировать, что означает слово «предел» на языке чисел. Строгое определение предела было сформулировано довольно поздно - только в середине XIX века. Дело в том, что в отличие от используемых ранее «назывных» определений (типа определения равнобедренного треугольника) здесь описывается процесс изменения величины: пробегая по ряду натуральных чисел `1,2,3,...,n,...`, мы наблюдаем за поведением `x_n`. Такие понятия плохо формализуются.
Попытаемся понять, что следует предпринять, чтобы проконтролировать утверждение «`x_n` стремится к `a`». Изобразим члены последовательности на числовой оси и отметим на ней точку `a`. Представим ситуацию образно: будем делать фотографии `a` каждый раз с новым оптическим увеличением. Число `a` будет пределом последовательности `(x_n)`, если `a` - «друг» `x_n`: на любой такой фотографии окажутся все `x_n`, начиная с некоторого номера.
Проиллюстрируем сказанное на примере последовательности `x_n=1//n`. В качестве «фотографии» `a=0` можно взять симметричный интервал `(-epsilon, epsilon)^1`. [1 `epsilon` - греческая буква «эпсилон».] Оптическому увеличению соответствует уменьшение `epsilon`. Пусть `k=1//epsilon`, тогда `1//n<epsilon` при `n>k` и, следовательно, член `x_n` попадает на «фотографию», т. е. `-epsilon<x_n<epsilon`. Например, при `epsilon1//100` все члены `x_(101), x_(102), ...`, окажутся в интервале `(-1//100, 1//100)`, при `epsilon=1//1000` уже только члены `x_(1001), x_(1002), ...`, окажутся в интервале `(-1//1000, 1//1000)` и т. д.
Число `a` называется пределом последовательности `(x_n)`, если для любого положительного числа `epsilon` найдётся такое действительное число `k`, что при всех `n>k` выполняется неравенство
`|x_n-a|<epsilon`. (2.1)
В этом случае пишут `lim_(n->oo) x_n=a` (читается: предел `x_n` при `n`, стремящемся к бесконечности, равен `a`). Последовательность, называется сходящейся, если существует число `a`, являющееся её пределом. Если такого числа `a` не существует, то последовательность называется расходящейся.
Часто в определении предела полагают число `k` натуральным. Однако, как нетрудно понять, получится эквивалентное определение.
Выясним геометрический смысл понятия предела. Для положительного числа `epsilon` интервал `(a-epsilon, a+epsilon)` называется `epsilon` - окрестностью точки `a`. Неравенство (2.1) равносильно двойному неравенству `-epsilon<x_n-a<epsilon` или
`a-epsilon<x_n<a+epsilon`. (2.2)
Неравенство (2.2) показывает, что все члены последовательности `(x_n)` с номерами `n>k` попадают в `epsilon` - окрестность точки `a`. В определении предела число `epsilon` может быть любым (сколь угодно малым), поэтому произвольная (сколь угодно малая) окрестность точки `a` содержит все члены `(x_n)` за исключением, быть может, конечного числа (рис. 1а). На уровне графика последовательности это означает, что вне сколь угодно узкой полосы между прямыми `x=a-epsilon` и `x=a+epsilon` может оказаться лишь конечное число точек графика `(x_n)` (рис. 1б).
В определении предела выбор числа `k`, вообще говоря, зависит от `epsilon`. Чтобы подчеркнуть это, иногда пишут `k=k(epsilon)`. Доказать, что последовательность `(x_n)` имеет предел, фактически означает найти функциональную зависимость `k` от `epsilon`. Вообще, определение предела по виду напоминает нескончаемую дискуссию между двумя лицами `A` и `B:A` задаёт точность приближения `epsilon`, в ответ `B` указывает число `k`, с которого эта точность достигается, т. е. выполняется неравенство (2.1) при всех `n>k`; уменьшает точность, `B` - указывает новое `k` и т. д.
Пусть `x_n=c` - постоянная последовательность. Доказать, что `lim_(n->oo)x_n=c`.
Пусть выбрано произвольное `epsilon>0`. Нам нужно найти такое число `k`, что при всех `n>k` выполнялось бы неравенство `|x_n-c|<epsilon`. Но это неравенство равносильно следующему: `|c-c|<epsilon`, или `0<epsilon`, что выполняется для всех номеров `n`. Это означает, что в качестве `k` можно выбрать любое число, например, `k=0`. Тогда для любого `n>k` имеет место неравенство `|x_n-c|<epsilon`. По определению `lim_(n->oo)x_n=c`.
В разобранном примере число `k` удалось выбрать так, чтобы оно годилось сразу для всех `epsilon`. Такой случай не типичен.
Доказать, что `lim_(n->oo)1/n=0`.
Пусть фиксировано произвольное `epsilon>0`. Нам нужно найти такое число `k`, что при всех `n>k` выполнялось бы неравенство `|1/n -0|<epsilon`, или `n>1//epsilon`. Выберем `k=1//epsilon`. Тогда при `n>k` имеем: `|1/n-0|=1/n<1/k=epsilon`. По определению `lim_(n->oo) 1/n=0`.
Наглядное представление о пределе можно получить, считая, что `x_n` - какие-то физические величины, которые мы можем измерять с определённой точностью, допускаемой приборами. Пусть `epsilon` есть точность прибора, тогда неравенство `|x_n-a|<epsilon` означает, что мы не сможем отличить `x_n` от `a`. Таким образом, условие `lim_(n->oo)x_n=a` означает, что при любой точности измерения последовательность `(x_n)`, начиная с некоторого номера, не отличается от постоянной последовательности `a`, `a`, `a`, `...` .
Могут ли два разных числа быть пределами одной и той же последовательности?
Нет. Предположим, что два разных числа `a` и `b` являются пределами одной и той же последовательности `x_n)` и пусть, например, `b>a`. Положим `epsilon=(b-a)//3`, тогда `epsilon` - окрестности точек `a` и `b` не пересекаются (сделать чертёж!). Ввиду условия найдутся такие числа `k_1` и `k_2`, что при всяком `n>k_1` член `x_n` лежит в `epsilon` -окрестности точки `a` и при всяком `n>k_2` член `x_n` лежит в окрестности точки `b`. Если теперь взять какое-нибудь `n>max{k_1,k_2}`, то окажется, что `x_n` лежит одновременно в `epsilon` - окрестности точки `a` и в `epsilon` - окрестности точки `b`, а это невозможно, поскольку окрестности не пересекаются.
Пусть `lim_(n->oo)x_n=a`. Имеет ли предел последовательность `(x_(n+1))`?
Пусть `lim_(n->oo)x_n=a`, `epsilon>o` - произвольное. По определению предела найдётся `k` такое, что `|x_n-a|<epsilon` при всех `n>k`. Но если номер `n>k`, то также `n+1>k` и, следовательно, `|x_(n+1)-a|<epsilon`. Это означает, что `lim_(n->oo)x_(n+1)=a`.
Пусть `lim_(n->oo)x_n=a`, `epsilon>o`. Можно ли утверждать, что найдётся такое число `k`, что `|x_n-a|<epsilon/2` при всех `n>k`?
Да. Поскольку `lim_(n->oo)x_n=a`, то по определению предела для любого положительного числа `alpha`, а следовательно, и для `alpha=epsilon//2`, найдётся число `k`, такое что `|x_n-a|<alpha` при всех `n>k`.
Сформулируем необходимое условие существования предела.
Если последовательность имеет предел, то она ограничена.
Пусть `lim_(n->oo)x_n=a`. Покажем, что последовательность `(x_n)` ограничена. Согласно примеру 1.4 для этого достаточно показать, что все её члены лежат на некотором отрезке. Возьмём `epsilon=1`. Тогда по определению предела найдётся число `k` такое, что все члены `(x_n)` с номерами `n>k` попадают в интервал `(a-1; a+1)`. За пределами этого интервала может оказаться лишь конечное число членов `x_1, x_2, ..., x_N`, где `N` - наибольший из номеров `n<=k`. Добавим к этому набору числа `a-1` и `a+1` и из полученного набора чисел выберем наименьшее (обозначим его через `m`) и наибольшее (обозначим его через `M`) Тогда отрезок `[m;M]` содержит уже все члены данной последовательности: `m<=x_n<=M` для всех `ninN`.
Доказать, что последовательность `x_n=n^2` не имеет предела.
В примере 1.6 было показано, что данная последователь-ность не является ограниченной. По теореме 2.1 заключаем, что последовательность `(x_n)` расходится.
Следующий пример показывает, что ограниченная последователь-ность может и не иметь предела, т. е. обратное утверждение к теореме 2.1 неверно.
Доказать, что последовательность `x_n=(-1)^n` не имеет предела.
Предположим противное, т. е. какое-то число `a` является пределом этой последовательности. Тогда для `epsilon=1` найдётся такое число `k`, что `|x_n-a|<1` при всех `n>k`. Пусть номер `N>k`, тогда `|x_N-a|<1` и `|x_(N+1)-a|<1`. Но одно из чисел `x_N` и `x_(N+1)` равно `1`, а другое равно `-1`. Поэтому `|-1-a|<1` и `|1-a|<1`, т. е. одновременно `0<a<2` и `-2<a<0`. Полученное противоречие показывает, что последовательность `(x_n)` расходится.
При вычислении пределов на практике редко пользуются опреде-лением. Обычно применяют уже известные стандартные предельные равенства и следующую теорему об арифметических операциях с пределами.
Если последовательности `(x_n)` и `(y_n)` сходятся, то сходятся и последовательности `(x_n+y_n)`, `(x_n*y_n)` и `x_n//y_n` (в последнем случае предполагается `y_n!=0`, `lim_(n->oo)y_n!=0`). При этом
1) `lim_(n->oo)(x_n+y_n)=lim_(n->oo)x_n+lim_(n->oo)y_n`;
2) `lim_(n->oo)(x_n*y_n)=(lim_(n->oo)x_n)*(lim_(n->oo)y_n)`;
3) `lim_(n->oo)(x_n)/(y_n)=(lim_(n->oo)x_n)/(lim_(n->oo)y_n)`.
Ограничимся доказательством пункта 2. Фиксируем произвольное `epsilon>0`. Нам нужно показать, что существует такое число `k`, что `|x_ny_n-ab|<epsilon` при всех `n>k`. По теореме 2.1 последовательности `(x_n)` и `(y_n)` ограничены; тем самым найдётся такое `C>0`, что `|x_n|<=C` и `|y_n|<=C` при всех `n`, а также `|a|<=C`, `|b|<=C`. Заметим, что
`|x_ny_n-ab|=|x_ny_n-x_nb+x_nb-ab|=|x_n(y_n-b)+b(x_n-a)|`
и, следовательно, по неравенству `|x+y|<=|x|+|y|` имеем
`|x_ny_n-ab|<=|x_n|*|y_n-b|+|b|*|x_n-a|`.
Ввиду условия существует число `k_1` такое, что `|x_n-a|<epsilon/(2C)` для всех `n>k_1`, а также число `k_2` такое, что `|y_n-b|<epsilon/(2C)` для всех `n>k_2`. Если положить `k=max{k_1,k_2}`, то при `n>k` имеем:
`|x_ny_n-ab|<=|x_n|*|y_n-b|+|b|*|x_n-a|<C epsilon/(2C)+C epsilon/(2C)=epsilon`,
что и требовалось.
Доказать, что постоянный множитель можно выносить за знак предела, т. е. `lim_(n->oo)cx_n=clim_(n->oo)x_n` для любого `cinR`.
В самом деле, рассмотрим последовательность `y_n=c`. Поскольку `lim_(n->oo)y_n=c` (пример 2.1), то по пункту 2 теоремы 2.2
`lim_(n->oo)cx_n=lim_(n->oo)c*lim_(n->oo)x_n=clim_(n->oo)x_n`.
Показать, что `lim_(n->oo) 1/(n^2)=0`.
Поскольку `lim_(n->oo) 1/n=0`, то по пункту 2 теоремы 2.2
`lim_(n->oo) 1/(n^2)=lim_(n->oo) 1/n*lim_(n->oo) 1/n=0`.
Теорему 2.2 можно обобщить на произвольное (конечное) число слагаемых (сомножителей). В частности, `lim_(n->oo)1/n^m=0` для любого `m inN`.
Найти `lim_(n->oo) ((n+2)^3-n(n-1)^2)/(n^2+11)`.
Обозначим дробь, стоящую под знаком предела, через `x_n`. В числителе и знаменателе `x_n` стоят последовательности, не являющиеся ограниченными (доказывается аналогично примеру 1.6). По теореме 2.1 они не имеют предела и теорема о пределе частного (теорема 2.2 3)) «напрямую» здесь неприменима. Поступим следующим образом: поделим числитель и знаменатель на наибольшую степень `n`. По формулам сокращённого умножения `(n+2)^3-n(n-1)^2=8n^2+11n+8`, так что `x_n` можно переписать в виде:
`x_n=(8n^2+11n+8)/(n^2+11)=(n^2(8+11/n + 8/n^2))/(n^2(1+11/n^2))=(8+11/n+8/n^2)/(1+11/n^2)`.
Теперь в числителе и знаменателе `x_n` стоят сходящиеся последовательности:
`lim_(n->oo)(8+11/n+8/n^2)=lim_(n->oo)8+11lim_(n->oo)1/n+8lim_(n->oo)1/n^2=8`,
`lim_(n->oo)(1+11/n^2)=lim_(n->oo)1+11lim_(n->oo)1/n^2=1`.
По пункту 3 теоремы 2.2
`lim_(n->oo)x_n=lim_(n->oo)(8+11/n+8/n^2)/(1+11/n^2)=(lim_(n->oo)(8+11/n+8/n^2))/(lim_(n->oo)(1+11/n^2))=8/1=8`.
`8`.
Следующее полезное свойство пределов известно под названием теоремы о «зажатой» последовательности.
Пусть `(x_n)`, `(y_n)` и `(z_n)` - такие последовательности, что `x_n<=y_n<=z_n` при всех `n inN` и `lim_(n->oo)x_n=lim_(n->oo)z_n=a`. Тогда `lim_(n->oo)y_n=a`.
Для данного `epsilon>0` существует такое число `k_1`, что члены `x_n` лежат в интервале `(a-epsilon, a+epsilon)` при всех `n>k_1`, и существует такое число `k_2`, что члены `z_n` лежат в интервале `a-epsilon;a+epsilon)` при всех `n>k_2`. Положим `k=max{k_1,k_2}`. Тогда при `n>k` одновременно `x_n in(a-epsilon;a+epsilon)` и `z_n in(a-epsilon;a+epsilon)` и, следовательно, `a-epsilon<x_n<=y_n<=z_n<a+epsilon`, т. е. `y_n in(a-epsilon;a+epsilon)`, что и требовалось.
Дана последовательность `x_n=1/(sqrt(n^2+1))+1/(sqrt(n^2+2))+...+1/(sqrt(n^2+n))`.
Доказать, что `lim_(n->oo)x_n=1`.
Попробуем «зажать» `x_n` между членами последовательностей, сходящихся к одному и тому же числу, и применим теорему 2.3.
Заметим, что `1/(sqrt(n^2+1))` - наибольшая, а `1/(sqrt(n^2+n))` - наименьшая дробь суммы `x_n`. Тогда верна оценка `n*1/(sqrt(n^2+n))<=x_n<=n*1/(sqrt(n^2+1))`.
Поскольку `n^2+n<n^2+2n+1`, тогда
`sqrt(n^2+n)<n+1 iff1/(sqrt(n^2+n))>1/(n+1) iff n/(sqrt(n^2+n))>n/(n+1)`.
Учитывая `n/(sqrt(n^2+1))<n/n=1`, получаем: `n/(n+1)<x_n<1`.
Поскольку `lim_(n->oo)n/(n+1)=1` и `lim_(n->oo)1=1`, по теореме 2.3 `lim_(n->oo)x_n=1`.
Если для любого `n inN`, `n>=n_0` выполняется неравенство `a_n<=b_n` и `lim_(n->oo)a_n=a`, `lim_(n->oo)b_n=b`, то `a<=b`.
Предположим, что `a>b`. По определению предела для `epsilon=(a-b)/2` найдутся такие `k_1`, `k_2`, что для `n>k_1` выполняется `|a_n-a|<epsilon`, а для `n>k_2` выполняется `|b_n-b|<epsilon`. Положим `k=max{k_1,k_2,n_0}`. Тогда для `n>k` имеем `b_n<b+epsilon=(a+b)/2=a-epsilon<a_n`, что противоречит условию.
Предельный переход не обязан сохранять строгие неравенства. Например, `1/n<0` для всех `n inN`, но `lim_(n->oo)1/n=0`.
В теории пределов важную роль играет следующий факт.
Всякая монотонная ограниченная последовательность имеет предел.
Эта теорема эквивалентна свойству полноты множества действительных чисел. Образно говоря, свойство полноты означает, что числовая ось является «сплошным» множеством, множеством без «дырок».
Доказать, что если `|q|<1`, то `lim_(n->oo)q^n=0`.
Для `q=0` утверждение очевидно. Пусть `q in (0,1)`, тогда
`x_(n+1)=q*x_n`, (2.3)
следовательно, `x_(n+1)<x_n` при всех `n`, т. е. последовательность `(x_n)` является строго убывающей. В частности, `x_n<x_1` при всех `n`. Кроме того, очевидно `x_n>0` при всех `n`, т. е. последовательность `(x_n)` ограничена. По теореме 2.5 существует `lim_(n->oo)x_n`. Обозначим его через `a`. Тогда, переходя к пределу в равенстве (2.3), получаем `a=q*a`, т. е. `a=0`.
Пусть теперь `q in (-1;0)`, тогда справедливо неравенство
`-|q|^n<=q^n<=|q|^n`.
Поскольку `|q|in(0;1)`, то по доказанному выше `lim_(n->oo)|q|^n=0`, тогда согласно примеру 2.5 и `lim_(n->oo)(-|q|^n)=0`. По теореме о «зажатой» последовательности (теорема 2.3) `lim_(n->oo)q^n=0`.
Дадим обоснование одного способа приближённого извлечения квадратных корней, встречавшегося еще в древних вавилонских текстах.
Последовательность `(x_n)` задана рекуррентно где
`x_(n+1)=1/2(x_n+a/x_n)`, (2.4)
`x_1>0`, `a>0`. Доказать, что `lim_(n->oo)x_n=sqrta`.
Поскольку `x_1>0` и `a>0`, все члены последовательности положительные. Применяя неравенство `(c+d)//2>=sqrt(cd)` для среднего арифметического и среднего геометрического, получаем:
`x_(n+1)=1/2(x_n+a/x_n)>=sqrt(x_na/x_n)=sqrta`,
т. е. `x_n>=sqrta` для всех `n>=2`. Отсюда вытекает, что
`x_(n+1)-x_n=(a-x_n^2)/(2x_n)<=0`,
т. е. последовательность `(x_n)` является нестрого убывающей при `n>=2`. Кроме того, `(x_n)` ограничена: `sqrta<=x_n<=x_2` для всех `n>=2`. По теореме 2.5 существует `lim_(n->oo)x_n=b` и по теореме 2.4 `b>=sqrta>0`. Переходя в равенстве (2.4) к пределу, получаем `b=1/2(b+a/b)`, откуда `b^2=a` и, значит, `b=sqrta`.

Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `ain R`, за исключением, быть может, самой точки `a`.
Число `A` называется пределом функции `y=f(x)` в точке `a`, если для любой последовательности `(x_n)` из области её определения такой, что `x_n!=a` и `lim_(n->oo)x_n=a` выполняется равенство `lim_(n->oo)f(x_n)=A`.
Обозначение: `lim_(n->oo)f(x)=A`, или `f(x)->A` при `x->a`.
В определении предела рассматриваются значения `x_n`, не равные `a`, поэтому в самой точке `a` функция `y=f(x)` может быть не определена; если значение `f(a)` определено, то оно не обязано совпадать с `A`. К тому же, поскольку последовательность `(f(x_n))` имеет не более одного предела, получаем, что если функция `y=f(x)` имеет предел при `x->a`, то этот предел единственный.
На рис. 2 изображена лишь одна последовательность `(x_n)`, которая к тому же является монотонной. Важно понимать, что `lim_(n->oo)f(x_n)=A` для любой последовательности `(x_n)` с условием `x_n!=a` и `lim_(n->oo)x_n=a`.
Доказать, что `lim_(n->oo)x=a`.
Очевидно, функция `f(x)=x` определена на любом интервале, содержащем `a`. Выберем произвольную последовательность `(x_n)` такую, что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда `f(x_n)=x_n` и, значит, `lim_(n->oo)f(x_n)=a`.
Доказать, что при `a>0lim_(n->a)sqrtx=sqrta`.
Функция `f(x)=sqrtx` определена при `x>=0` и, следовательно, определена на некотором интервале, содержащем `a`. Выберем произвольную последовательность неотрицательных чисел `x_n!=a`, что `lim_(n->oo)x_n=a`. Нам нужно показать, что `lim_(n->oo)sqrtx_n=sqrta`. Фиксируем произвольное `epsilon>0`, тогда найдётся такое число `k`, что при `n>k` выполняется неравенство `|x_n-a|<epsilonsqrta`. Следовательно,
`|sqrtx_n-sqrta|=(|(sqrt(x_n)-sqrta)(sqrt(x_n)+sqrta)|)/(sqrt(x_n)+sqrta)<(|x_n-a|)/(sqrta)<epsilon`,
что и требовалось.
Доказать, что `lim_(x->1)(x^2-1)/(x-1)=2`.
Функция `f(x)=(x^2-1)/(x-1)` определена на любом интервале, содержащем `x=1`, кроме этой точки. Поскольку при `x!=1` имеет место равенство `f(x)=x+1`, то для любой последовательности `(x_n)` такой, что `x_n!=1` и `lim_(n->oo)x_n=1` выполняется `lim_(n->oo)f(x_n)=lim_(n->oo)x_n+1=2`.
Пусть функции `y=f(x)`, `y=g(x)` определены на некотором интервале, содержащем точку `a in R`, за исключением, быть может, самой точки `a`, `lim_(x->a)f(x)=A` и `lim_(x->a)g(x)=B`. Тогда
1) `lim_(x->a)(f(x)+g(x))=A+B`;
2) `lim_(x->a)f(x)g(x)=AB`;
3) если дополнительно `g(x)!=0` при `x!=a`, `B!=0`, то `lim_(x->a)(f(x))/(g(x))=A/B`.
Эти свойства вытекают из арифметических операций над пределами последовательностей (теорема 2.2). Приведём доказательство для свойства 2. Остальные доказываются аналогично.
Пусть некоторая произвольная последовательность `(x_n)` из интервала, на котором определены функции, такова что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда по определению предела функции `lim_(n->oo)f(x_n)=A` и `lim_(n->oo)g(x_n)=B`. По пункту 2 теоремы 2.2 `lim_(n->oo)f(x_n)g(x_n)=AB`. По определению предела функции получаем, что `lim_(x->a)f(x)g(x)=AB`.
Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `a`. Функция `y=f(x)`называется непрерывной в точке `a`, если `lim_(x->a)f(x)=f(a)`, т. е. если для любой последовательности `(x_n)` из области определения функции такой, что `lim_(n->oo)x_n=a`, выполняется равенство `lim_(n->oo)f(x_n)=f(a)`.
Отметим два обстоятельства, связанных с определением непрерывности. Во-первых, оговорка `x_n!=a` здесь не нужна, т. к. при `x_n=a` значения `f(x_n)` равны `f(a)`. Во-вторых, важно понимать, что если функция `y=f(x)` непрерывна в точке `a`, то
1) она определена в точке `a`;
2) существует `lim_(x->a)f(x)=A` и
3) `A=f(a)`.
Если хотя бы один из пунктов 1) – 3) не выполнен, то функция не является непрерывной в точке `a`.
Многочлен является непрерывной на всей числовой прямой функцией.
Пусть `P(x)=a_nx^n+a_(n-1)x^(n-1)+...+a_1x+a_0` - многочлен степени `n, a in R`. Нам нужно показать, что `lim_(x->a)P(x)=P(a)`. В силу примера 3.1 `lim_(x->a)x=a`,, а в силу примера 2.1 для константы `c` ‑ `lim_(x->a)c=c`. Последовательно применяя пункт 2 теоремы 3.1, получаем, что `lim_(x->a)cx^m=ca^m` при любом натуральном `m`. Осталось `n+1` раз применить пункт 1 теоремы 3.1 и заключить, что `lim_(x->a)P(x)=P(a)`.
Из теоремы 3.1 вытекает, что если функции `y=f(x)`, `y=g(x)` непрерывны в точке `a`, то функции `y=f(x)+-g(x)`, `y=f(x)g(x)`, `y=f(x)//g(x)` `(g(a)!=0)` также непрерывны в `a`.
Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
Функция `y=|x|` непрерывна на всей числовой прямой.
Функция `y=|x|` на промежутке `(-oo;0)` совпадает с функцией `y=-x`, а на промежутке `(0;+oo)` - с функцией `y=x`, которые непрерывны на этих промежутках. Осталось исследовать на непрерывность данную функцию в точке `x=0`. Поскольку `||x_n|-0|=|x_n-0|`, то для любой последовательности `(x_n)` такой, что `lim_(n->oo)x_n=0` верно `lim_(n->oo)|x_n|=0`. По определению `lim_(x->0)|x|=0`, функция `y=|x|` непрерывна в точке `x=0`.
Вообще, все элементарные функции, изучаемые в школьном курсе, непрерывны в каждой точке, в окрестности которой эти функции определены.
Найти `lim_(x->2)(x^3+sqrt((x-3)^2)+11)`.
Поскольку `sqrt((x+3)^2)=|x-3|` и `|x-3|=3-x` при `x<=3`,
то `f(x)=x^3+|x-3|+11=x^3-x+14` при `x<=3`.
Многочлен `P(x)=x^3-x+14` непрерывен на всей числовой прямой, и в частности, в точке `x=2`. Поэтому `lim_(x->2)f(x)=P(2)=2^3-2+14=20`.
Найти `lim_(x->5)(sqrt(x-1)-2)/(x-5)`.
Обозначим дробь, стоящую под знаком предела, через `f(x)`. В числителе и знаменателе дроби `f(x)` стоят функции, непрерывные в точке `x=5`. Предел этих функций при `x->5` равен их значению в точке `x=5`, т. е. равен `0`. В этом случае говорят, что имеет место неопределённость `(0/0)`. Для её «раскрытия» приходится прибегнуть к искусственному приёму – умножению числителя и знаменателя дроби `f(x)` на «сопряжённое выражение» `sqrt(x-1)+2`:
`lim_(x->5)f(x)=lim_(x->5)((sqrt(x-1)-2)(sqrt(x-1)+2))/((x-5)(sqrt(x-1)+2))=`
`=lim_(x->5)(x-5)/((x-5)(sqrt(x-1)+2))=`
`=lim_(x->5)1/(sqrt(x-1)+2)=1/(sqrt(5-1)+2)=1/4`.
Предпоследнее равенство получено в силу непрерывности функции `y=1/(sqrt(x-1)+2)` в точке `x=5`.
`1/4`.

Пусть функция `y=f(x)` определена на некотором интервале `(c;d)`, содержащем точку `ainR`. Функция `y=f(x)` называется дифференцируемой в точке , если существует конечный
`lim_(x->a)(f(x)-f(a))/(x-a)`.
Этот предел называется производной функции `y=f(x)` в точке `a` и обозначается `f^'(a)`.
Для точек `x,ain(c;d)` введём обозначения: `Deltax=x-a` – приращение аргумента; `Deltaf=f(x)-f(a)` – приращение функции. Тогда дифференцируемость `y=f(x)` в точке `a` означает, что
`f^'(a)=lim_(x->a)(Deltaf)/(Deltax)`.
Функция называется дифференцируемой на множестве, если она дифференцируема в каждой точке этого множества.
Найти по определению производные функций:
а) `f(x)=c, cinR`, в произвольной точке;
б) `f(x)=x^n,ninN`, в произвольной точке;
в) `f(x)=sqrtx` в точке `a>0`.
а) Пусть `ainR`. Поскольку приращение постоянной функции `Deltaf=c-c=0`, то производная `f^'(a)=lim_(x->a)0/(x-a)=0`.
б) Приращение данной функции в точке `ainR` можно записать следующим образом: `Deltaf=x^n-a^n=(x-a)(x^(n-1)+ax^(n-2)+...+a^(n-1))`. Тогда
`f^'(a)=lim_(x->a)(x^n-a^n)/(x-a)=lim_(x->a)(x^(n-1)+ax^(n-2)+...+a^(n-1))=na^(n-1)`.
Итак, `(x^n)^'=nx^(n-1)` для всех `xinR`.
в) Пусть `a>0`. Функция `s(x)=sqrtx` определена на некотором интервале, содержащем `a` (например, `(a//2,2a)`). Запишем отношение приращений
`(Deltaf)/(Deltax)=(sqrtx-sqrta)/(x-a)=(sqrtx-sqrta)/((sqrtx-sqrta)(sqrtx+sqrta))=1/(sqrtx+sqrta)`.
Тогда `f^'(a)=lim_(x->a)1/(sqrtx+sqrta)=1/(2sqrta)`, т. е. `(sqrtx)=1/(2sqrtx)` при `x>0`.
Укажем физический смысл производной. Пусть `s=s(t)` - расстояние, пройденное телом за время `t` (движение одномерное). Тогда частное `(s(t)-s(t_0))/(t-t_0)` выражает среднюю скорость за время от `t_0` до `t`. Если мы хотим узнать скорость тела в момент времени `t_0`, то нужно неограниченно уменьшать промежуток от `t_0` до `t`, т. е. устремлять `t` к `t_0`. Таким образом, `s^'(t_0)=lim_(t->t_0)(s(t)-s(t_0))/(t-t_0)` есть мгновенная скорость в `t_0`. Так что интуитивное представление о производной есть у каждого, кто видел спидометр автомобиля.
Если функция `y=f(x)` дифференцируема в точке `a`, то она непрерывна в точке `a`.
Следующий пример показывает, что обратное утверждение к теореме 4.1 неверно.
Доказать, что функция `y=|x|` не дифференцируема (не имеет производной) в точке `x=0`.
Рассмотрим две последовательности `(x_n)` и `(bar(x)_n)` такие что `x_n->0`, `bar(x)_n->0` при `n->oo`, все `x_n>0`, а все `barx_n<0`. Тогда соответствующие отношения приращений функции к приращениям аргумента в точке `x=0` имеют вид `((Deltay)/(Deltax))_n=(|x_n|-0)/(x_n-0)=(x_n)/(x_n)=1` и `((Deltay)/(Deltax))_n=(|barx_n|-0)/(barx_n-0)=(-barx_n)/(barx_n)=-1` что означает отсутствие предела `lim_(x->0)(Deltay)/(Deltax)`, т. е. отсутствие `y^'(0)`.
Пусть функции `y=f(x)`, `y=g(x)` дифференцируемы в точке `a`, тогда в этой точке дифференцируемы функции `y=(f+g)(x)`, `y=c*f(x)` (где `cinR`), `y=(f*g)(x)` и, если `g(a)!=0`, то также `y=(f/g)(x)`,причём
1) `(f+-g)^'(a)=f^'(a)+-g^'(a)` и `(c*f)^'(a)=c*f^'(a)`;
2) `(f*g)^'(a)=f^'(a)g(a)+f(a)g^'(a)`;
3) `(f/g)^'(a)=(f^'(a)g(a)-f(a)g^'(a))/(g^2(a))`.
Из теоремы 4.2 и пунктов а) и б) примера 4.1 вытекает
Любой многочлен `P(x)=a_nx^n+a_(n-1)x^(n-1)+...+a_1x+a_0` является дифференцируемой на `R` функцией с производной `P^'(x)=a_n nx^(n-1)+a_(n-1)(n-1)x^(n-2)+...+a_1`.
Найти производную функции `y=(x+1)/(3x-6)` при `x!=2`.
На основании примера 4.1 и теоремы 4.2 получаем:
`y^'((x+1)^'(3x-6)-(x+1)(3x-6)^')/((3x-6)^2)=`
`=(3x-6-(x+1)*3)/(9(x-2)^2)=(-1)/((x-2)^2)`.
Вообще говоря, любая дробно-рациональная функция дифференцируема во всех точках, за исключением нулей знаменателя.
Пусть на множестве `X` задана функция `y=f(x)` и на множестве её значений задана функция `z=g(y)`. Тогда говорят, что на множестве `X` определена сложная функция (или композиция) `z=g(f(x))` функций `z=g(y)` и `y=f(x)`. Например, рассмотрим на луче `X=(-oo;-1]` функцию `y=x^2-1`. На множестве её значений `[0;+oo)` определена функция `z=g(y)=sqrty`. Тогда на `X` можно определить сложную функцию `z=g(f(x))=sqrt(x^2-1)`.
Пусть на множестве `X` определена сложная функция `z=g(f(x))`. Если функция `y=f(x)` дифференцируема в точке `x_0`, а функция `z=g(y)` дифференцируема в точке `y_0=f(x_0)`, то сложная функция `z=g(f(x))` дифференцируема в точке `x_0` и `(g(f(x_0)))^'=g(y_0)f^'(x_0)`.
Найти производную функции `z(x)=sqrt(x^2-1)` в точке `x in(-oo;-1)`.
Данная функция является композицией двух функций `g(y)=sqrty` и `y=f(x)=x^2-1`. Поскольку `g^'(y)=1/(2sqrty)` (см. пример 4.1), а `y^'=f^'(x)=2x`, то по теореме 4.3 получаем
`z^'(x)=g^'(f(x))*f^'(x)=(1)/(2sqrt(f(x)))*f^'(x)=`
`=(2x)/(2sqrt(x^2-1))=x/(sqrt(x^2-1))`.
Пусть функция `y=f(x)` дифференцируема в точке `a`. Касательной к графику `f` в точке `A(a;f(a))` называется прямая, проходящая через точку `A`, угловой коэффициент которой равен `f^'(a)`. Уравнение касательной в точке `A` имеет вид
`y=f(a)+f^'(a)(x-a)`.
Функция `f(x)=sqrt(1-x^2)` дифференцируема в каждой точке интервала `(-1;1)` с `f^'(x)=-x/(sqrt(1-x^2))`. Следовательно, уравнение касательной к графику этой функции в `A(a;f(a))` имеет вид `y=sqrt(1-a^2)-(a(x-a))/(sqrt(1-a^2))`, т. е. `y=(1-ax)/(sqrt(1-a^2)`. График `f` представляет собой полуокружность, а касательная к этой кривой была определена в геометрии. Докажем, что оба определения дают одну и ту же прямую.
Рассмотрим случай `ain(0;1)`. Касательная, определенная при помощи производной, проходит через точку `A(a;f(a))` и угловой коэффициент её равен `f^'(a)=-a/(sqrt(1-a^2))`. Так как этот угловой коэффициент отрицателен, то угол `varphi`, образованный касательной с положительным направлением оси `Ox`, тупой: `"tg"varphi=f^'(a)`. Тогда тангенс острого угла `alpha` (см. рис. 3), образованного касательной с отрицательным направлением оси `Ox`, равен `a/(sqrt(1-a^2))`. Котангенс же острого угла `beta`, образованного прямой `OA` с положительным направлением оси `Ox`, равен `a/(f(a))=a/(sqrt(1-a^2))`. Итак, `"tg"alpha="ctg"beta`, оба угла `alpha` и `beta` острые, поэтому `beta=90^@-alpha`. А это значит, что касательная, определенная при помощи производной, перпендикулярна радиусу окружности, проведенному в точку `A`, т. е. совпадает с касательной в смысле геометрического определения. Случай `ain(-1;0)` рассматривается аналогично. Этот случай (а также случай `a=0`) рекомендуем рассмотреть самостоятельно.
Часто требуется провести касательную к графику функции через произвольную точку плоскости. Такая задача может иметь два и более решений, а может и вообще не иметь решений.
Провести касательную к параболе `y=1+2x-x^2` через произвольную точку плоскости `(x_0;y_0)`. Исследовать решение.
Так как `(1+2x-x^2)^'=2-2x`, то уравнение касательной к параболе в точке `(a;1+2a-a^2)` имеет вид:
`y=(1+2a-a^2)+(2-2a)(x-a)`.
Эта касательная должна проходить через точку `(x_0;y_0)`, откуда `y_0=(1+2a-a^2)+(2-2a)(x_0-a)` и после преобразований получаем уравнение для нахождения абсциссы точки касания `a`:
`a^2-2x_0a+(1+2x_0-y_0)=0`. (*)
Если `D/4=x_0^2-2x_0-1+y_0<0`, т. е. `y_0<1+2x_0-x_0^2`, то уравнение (*) не имеет решений.
Если `D/4>0`, т. е. `y_0>1+2x_0-x_0^2`, то уравнение (*) имеет два решения `a=x_0+-sqrt(x_0^2-2x_0-1+y_0)`. Подставляя найденные `a` получим уравнения двух касательных, проходящих через точку `(x_0;y_0)`. Например, при `x_0=0`, `y_0=2` имеем `a+-1` и соответственно уравнения двух касательных: `y=2` (горизонтальная касательная, касающаяся параболы в её вершине `(1;2)`) и `y=4x+2` (наклонная касательная, касающаяся параболы в точке `(-1;-2)`, см. рис. 4). Наконец, если `D/4=0` т. е. `y_0=1+2x_0-x_0^2`, то уравнение имеет одно решение `a=x_0`. Геометрический смысл решения очень прост.
Если `y_0<1+2x_0-x_0^2`, т. е. точка `(x_0;y_0)` лежит «ниже» параболы, то через эту точку касательную провести нельзя.
Если `y_0>1+2x_0-x_0^2`, т. е. точка `(x_0;y_0)` лежит «выше» параболы, то через эту точку можно провести две касательные к параболе. Наконец, если `y_0=1+2x_0-x_0^2`, т. е. точка `(x_0;y_0)` лежит на параболе, то через нее можно провести единственную касательную, касающуюся параболы в точке `(x_0;y_0)`.

Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `ainR`. Точка `a` называется точкой локального максимума функции `f`, если существует `epsilon` - окрестность точки `a` что для любого `x!=a` из этой окрестности `f(x)<f(a)`.
Если выполнено неравенство `f(x)>f(a)`, то `a` называется точкой локального минимума функции `f`.
Точки локального максимума и локального минимума называют точками локального экстремума.
Если точка `a` является точкой локального экстремума функции `y=f(x)` и функция `f` имеет производную в этой точке, то `f^'(a)=0`.
Физический смысл: при одномерном движении с возвращением в точке максимального удаления должна быть остановка. Геометрический смысл: касательная в точке локального экстремума горизонтальна.
Из теоремы Ферма следует, что если функция имеет экстремум в точке `a`, то в этой точке производная функции либо равна нулю, либо не существует. Например, функция `y=|x|` имеет минимум в точке `x=0`, а производная в этой точке не существует (см. пример 4.2). Точки, в которых функция определена, а производная равна нулю или не существует, будем называть критическими.
Итак, если у функции имеются точки экстремума, то они лежат среди критических точек (критические точки «подозрительны» на экстремум). Для формулировки условий, обеспечивающих наличие экстремума в критической точке, нам потребуется следующее понятие.
Напомним, что под промежутком понимается интервал (конечный или бесконечный), полуинтервал или отрезок числовой прямой.
Пусть функция `y=f(x)` определена на промежутке `I`.
1) Функция `y=f(x)` возрастает на `I`, если для любых `x,yinI`, `x<y`, выполняется `f(x)<f(y)`.
2) Функция `y=f(x)` убывает на `I`, если для любых `x,yinI`, `x<y`, выполняется `f(x)>f(y)`.
Если функция возрастает или убывает на `I`, то говорят, что функция монотонна на промежутке `I`.
Условия монотонности. Пусть функция `y=f(x)` определена на промежутке `I` с концами `a`, `b`, дифференцируема на `(a, b)` и непрерывна в концах, если они принадлежат `I`. Тогда
1) если `f^'(x)>0` на `(a, b)`, то функция возрастает на `I`;
2) если `f^'(x)<0` на `(a, b)`, то функция убывает на `I`.
Условия экстремума. Пусть функция `y=f(x)` определена на интервале `(ab)`, непрерывна в точке `x_0 in(a, b)` и дифференцируема на `(a,x_0) uu (x_0,b)`. Тогда
1) если `f^'(x)>0` на `(a;x_0)` и `f^'(x)<0` на `(x_0;b)`, то `x_0` - точка локального максимума функции `f`;
2) если `f^'(x)<0` на `(a;x_0)` и `f^'(x)>0` на `(x_0;b)`, то `x_0` - точка локального минимума функции `f`.
Исследовать функцию `y=x^3-3x` на монотонность и экстремумы на области определения.
Данная функция определена на `R` и дифференцируема в каждой точке (см. следствие теоремы 4.2), причём `y^'=3(x^2-1)`. Так как `y^'<0` при `x in(-1,1)`; `y^'>0` при `x in(-oo,-1)uu(1,+oo)`, то функция возрастает на лучах `(-oo,-1]` и `[1,+oo)` (на каждом из двух лучей в отдельности, но не на их объединении!), убывает на отрезке `[-1,1]`. По условию экстремума `x=-1` - точка локального максимума, а `x=1` - точка локального минимума. Так как `y^'=0` только в точках `x=1` и `x=-1`, то по теореме Ферма других точек экстремума у функции нет.
Рассмотрим важный класс задач, в которых используется понятие производной – задачи нахождения наибольшего и наименьшего значения функции на отрезке.
Найти наибольшее и наименьшее значение функции `y=x^3-3x` на отрезке: а) `[-2;0]`; б) `[1;3]`.
а) Из примера 5.1 следует, что функция возрастает на `(-oo,-1]` и убывает на `[-1,1]`. Так что `y(-1)>=y(x)` при всех `x in[-2;0]` и `y_"наиб"=y(-1)=2` - наибольшее значение функции на отрезке `[-2;0]`. Чтобы найти наименьшее значение, нужно сравнить значения функции на концах отрезка. Поскольку `y(-2)=-2`, а `y(0)=0`, то `y_"наим"=-2` - наименьшее значение функции на отрезке `[-2;0]`.
б) Так как на луче `[1,+oo)` функция возрастает, то `y(1)<=y(x)<=y(3)` для всех `x in[1;3]`, поэтому `y_"наим"=y(1)=-2`, `y_"наиб"=y(3)=18`.
Отметим, что непрерывная на отрезке функция всегда имеет наибольшее и наименьшее значение.
Найти наибольшее и наименьшее значение функции `y=x^3-12|x+1|` на отрезке `[-4;3]`.
Отметим, что функция непрерывна на всей числовой прямой. Обозначим `f_1(x)=x^3+12(x+1)`, `f_2(x)=x^3-12(x+1)`. Тогда `y=f_1(x)` при `-4<=x<=-1` и `y=f_2(x)` при `-1<=x<=3`. Находим `f_1^'(x)=3x^2+12`, `f_2^'(x)=3x^2-12`. Уравнение `f_1^'(x)=0` не имеет действительных корней, а уравнение `f_2^'(x)=0` имеет два действительных корня `x_1=-2`, `x_2=2`, из которых интервалу `(-1;3)` принадлежит только точка `x_2`. В точке `x=-1` функция определена, но не имеет производной (можно, например, провести рассуждения, аналогичные рассуждениям примера 4.2). Итак, имеется две критические точки: `x=-1` и `x=2`. Производная `y^'(x)=f_1^'(x)>0` на `(-4;-1)`, `y^'(x)=f_2^'(x)<0` на `(-1;2)` и `y^'(x)=f_2^'(x)>0` на `(2;3)`. Запишем все исследования в таблице:
| `x` | `x=-4` | `(-4;-1)` | `x=-1` | `(-1;2)` | `x=2` | `(2;3)` | `x=3` |
| `y^'` |
|
`+` |
не сущ. |
`-` |
`0` |
`+` |
|
| `y` | `-100` |
возр. |
`-1` макс. |
убыв. |
`-28` мин. |
возр. |
`-21` |
`y_"наиб"=-1`; `y_"наим"=-100`.

Одним из разделов школьной математики является изучение функциональных зависимостей или функций.
Напомним, что функцией математики называют зависимость величины от одной или нескольких других величин. При этом независимые переменные величины принято называть аргументами, а зависимые – функциями. При этом важно не забывать, что каждому значению аргумента (или аргументов) ставится в соответствие единственное значение зависимой переменной (функции). Наглядно функции изображают с помощью графика – специального набора точек на плоскости. Пусть имеется функция $$ y=f\left(x\right)$$ одной переменной $$ x$$. На плоскости введём декартову систему координат $$ xOy$$ и рассмотрим множество точек $$ G$$ с координатами $$ (x,f(x\left)\right)$$, где $$ x$$ принадлежит некоторому множеству $$ M$$, которое называется областью определения функции. А множество $$ G$$ называется графиком функции $$ y=f\left(x\right)$$ (рис. 1).
В школьном курсе математики вы изучали такие типы функций:
График линейной функции можно построить по двум точкам, поскольку это прямая линия. Однако стоит заметить, что не всякая прямая будет графиком линейной функции. Если взять вертикальную прямую $$ x=a$$, то такая линия не может быть графиком никакой функции (рис. 2).
Действительно, здесь одному значению переменной $$ x$$ ставится в соответствие несколько значений переменной $$ y$$. Итак,
прямая на плоскости $$ xOy$$ – график некоторой линейной функции тогда и только тогда, когда она не вертикальна.
Напомним геометрический смысл коэффициентов $$ k$$ и $$ b$$ в уравнении прямой $$ y=kx+b:$$ $$ k=\mathrm{tg} \alpha $$ – тангенс угла наклона прямой к оси $$ Ox$$, $$ b$$ – ордината точки пересечения прямой с осью $$ Oy$$. Поэтому две невертикальные прямые $$ y={k}_{1}x+{b}_{1}$$ и $$ y={k}_{2}x+{b}_{2}$$:
Условие перпендикулярности прямых несложно пояснить. Рассмотрим пару прямых, параллельных данным и проходящих через начало координат (см. рис. 3).
Из перпендикулярности этих прямых следует, что $$ \alpha =\phi $$. Поэтому если точка $$ A({a}_{0};{b}_{0})$$ лежит на первой прямой, то точка $$ B(-{b}_{0};{a}_{0})$$ лежит на второй. Ясно, что можно подобрать $$ {a}_{0}\ne 0$$ и $$ {b}_{0}\ne 0$$, откуда $$ {k}_{1}{k}_{2}={\displaystyle \frac{{b}_{0}}{{a}_{0}}}·{\displaystyle \frac{{a}_{0}}{-{b}_{0}}}=-1$$.
Теперь напомним основные сведения о функциях вида $$ f\left(x\right)=a{x}^{2}+bx+c$$.
Сразу отметим, что такая функция квадратична только при $$ a\ne 0$$. В случае же $$ a=0$$ эта функция квадратичной уже не будет. Если в задаче возможна такая ситуация, то случай $$ a=0$$ обязательно нуждается в отдельном рассмотрении. Нужно всегда обращать на это внимание!
Будем считать, что $$ a\ne 0$$. Тогда графиком функции $$ y=f\left(x\right)$$ будет парабола. Такие графики принято строить схематично, учитывая следующее:
Теперь поговорим о графиках степенной функции. Легко убедиться, что график функции
$$ f\left(x\right)={x}^{n}$$ ($$ n\in N$$) при $$ x\ge 0$$
выглядит так, как показано на рис. 4. Для чётных $$ n$$, очевидно, верно $$ f(-x)=f\left(x\right)$$, а для нечетных $$ n$$ верно $$ f(-x)=-f\left(x\right)$$ для всякого $$ x$$. Поэтому в зависимости от чётности $$ n$$ графики функции $$ f\left(x\right)={x}^{n}$$ имеют такой вид (рис. 5 и 6).
Напомним, что функция, область допустимых значений которой симметрична относительно начала координат, называется чётной, если справедливо равенство $$ f(-x)=f\left(x\right)$$ и нечётной, если $$ f(-x)=-f\left(x\right)$$. Наример, нетрудно проверить, что функция
$$ f\left(x\right)=|x-2|+|x+2|$$ – чётная,
а функция
$$ g\left(x\right)=|x-2|-|x+2|$$ – нечётная.
В случае нечётного $$ n$$ график симметричен относительно начала координат. Такие функции называют нечётными (рис. 5). Если же $$ n$$ четно, то график симметричен относительно оси ординат. Такие функции называют чётными (рис. 6).
Для построения графика $$ f\left(x\right)=\sqrt[n]{x}$$ нужно записать уравнение $$ y=\sqrt[n]{x}$$ или $$ x={y}^{n}$$. Это означает, что график имеет вид линии $$ y={x}^{n}$$, но при этом $$ x$$ и $$ y$$ меняются местами. Для чётных $$ n$$ при этом еще нужно учесть ОДЗ $$ x\ge 0$$. Поэтому график функции $$ f\left(x\right)=\sqrt[n]{x}$$ имеет следующий вид в зависимости от чётности натурального числа $$ n$$ (рис. 7, 8):
Рассмотрим теперь функции вида $$ f\left(x\right)=\frac{k}{x}$$.
Поскольку функция $$ f$$ нечётна, то график должен быть симметричным относительно начала координат. Схематический вид графика этой функции показан на рисунке 9.
Если $$ k<0$$, то график функции $$ y={\displaystyle \frac{k}{x}}$$ имеет примерно такой же вид, и его можно получить симметрией относительно оси $$ Oy$$ из графика функции $$ y={\displaystyle \frac{\left|k\right|}{x}}$$ (рис. 10).
Покажем, как меняется график функции $$ f\left(x\right)={\displaystyle \frac{k}{x}}$$ при изменении параметра $$ k$$. Если $$ \left|{k}_{2}\right|>\left|{k}_{1}\right|$$, то линия $$ f\left(x\right)={\displaystyle \frac{{k}_{2}}{x}}$$ более удалена от осей координат, чем $$ f\left(x\right)={\displaystyle \frac{{k}_{1}}{x}}$$. Схематично это изображено на рис. 11, 12.